Galvagni Figures for Polypents
A polypent is a figure made of regular pentagons joined
edge to edge.
A Galvagni figure is a figure that can be tiled by a polyform
in more than one way—a kind of self-compatibility figure.
Galvagni figures first appeared in Erich Friedman's
Math Magic
for November 2004.
Many of the polypent Galvagni figures up to order 5 were found by
Scott Reynolds or Erich Friedman.
Here are minimal known Galvagni figures for polypents.
The black tiles have no Galvagni figures.
The gray tiles have no known Galvagni figures.



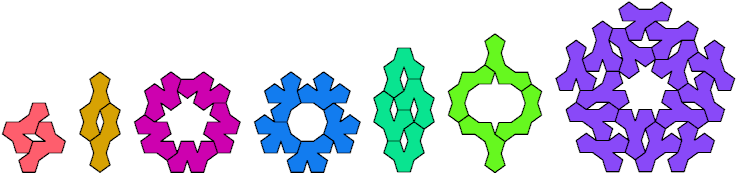
Hypersymmetric Variants


Hypersymmetric Variants
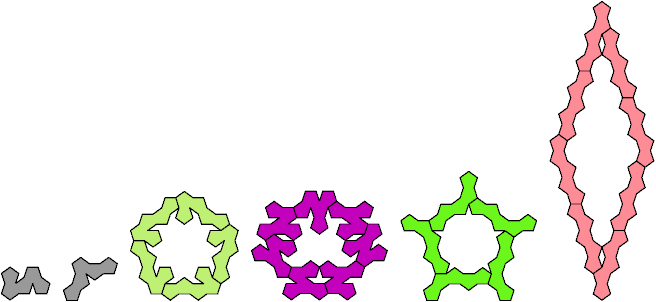
Joint Solutions
No hypersymmetric variant is known for the V and Z pentapents.
The X pentapent has no solution at all.
We can make quasi-Galvagni Figures by pairing them:
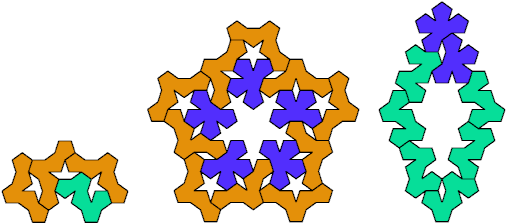
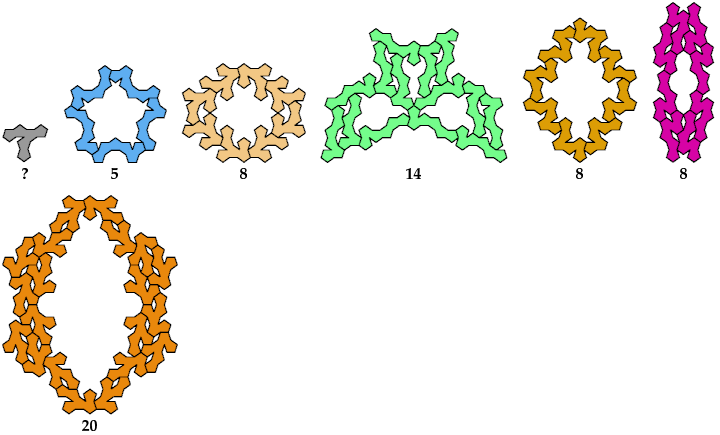
Two to four tiles

Five tiles

Six or more tiles

Unsolved

Hypersymmetric Variants
Last revised 2023-03-31.
Back to Galvagni Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]













