
A pentahex is a polyhex with 5 cells. There are 22 pentahexes, independent of rotation and reflection:

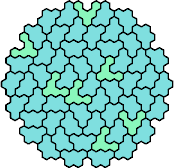
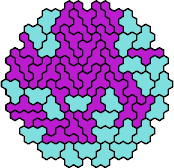
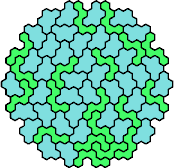
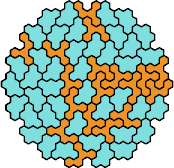
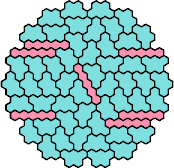
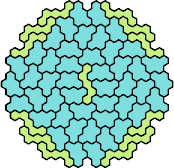
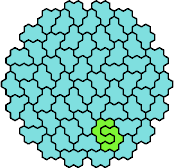
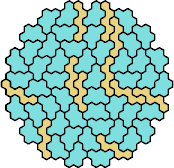
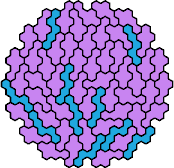
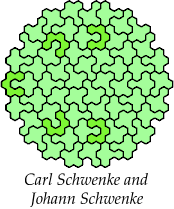
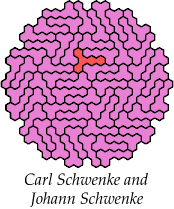
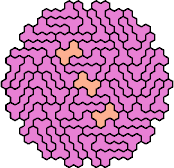
There are 231 pairs of pentahexes. Here I show how a polyhex with 295 cells and full symmetry can be tiled with at least 166 of these pairs, using at least one of each tile of the pair.
See also Pentomino Pair Oddities.
If you solve an unsolved case, please write.
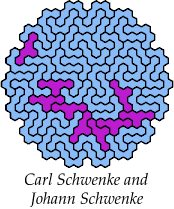
Carl Schwenke and Johann Schwenke found many of these tilings.
| 5AD | 5AF | 5AH | 5AK | 5AL |
|---|---|---|---|---|
| 
| 
| 
| 
|
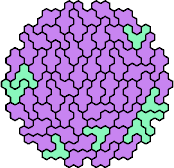
| 5AN | 5AP | 5AQ | 5AR | 5AS |

| 
| 
| 
| 
|
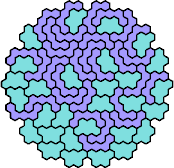
| 5AY | 5AZ | 5CD | 5CF | 5CK |

| 
| 
| 
| 
|
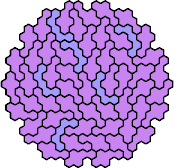
| 5CL | 5CN | 5CP | 5CR | 5CY |

| 
| 
| 
| 
|
| 5CZ | 5DE | 5DF | 5DH | 5DI |

| 
| 
| 
| 
|
| 5DJ | 5DK | 5DL | 5DN | 5DP |

| 
| 
| 
| 
|
| 5DQ | 5DR | 5DS | 5DT | 5DU |

| 
| 
| 
| 
|
| 5DV | 5DW | 5DX | 5DY | 5DZ |
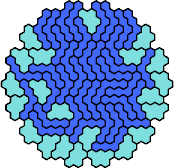
| 
| 
| 
| 
|
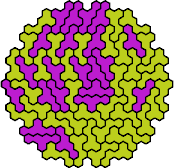
| 5EF | 5EH | 5EJ | 5EK | 5EL |

| 
| 
| 
| 
|
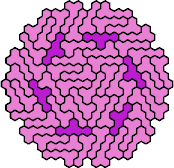
| 5EN | 5EP | 5ER | 5EY | 5EZ |

| 
| 
| 
| 
|
| 5FH | 5FJ | 5FK | 5FL | 5FN |

| 
| 
| 
| 
|
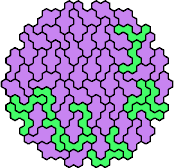
| 5FP | 5FQ | 5FR | 5FS | 5FT |
| 
| 
| 
| 
|
| 5FU | 5FW | 5FX | 5FY | 5FZ |

| 
| 
| 
| 
|
| 5HK | 5HL | 5HN | 5HP | 5HQ |
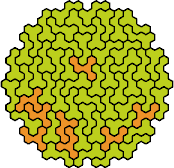
| 
| 
| 
| 
|
| 5HR | 5HS | 5HU | 5HV | 5HX |

| 
| 
| 
| 
|
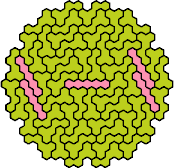
| 5HY | 5HZ | 5IK | 5IL | 5IN |

| 
| 
| 
| 
|
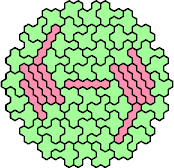
| 5IP | 5IQ | 5IR | 5IY | 5IZ |
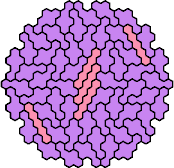
| 
| 
| 
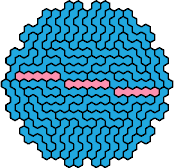
| 
|
| 5JK | 5JL | 5JN | 5JP | 5JQ |

| 
| 
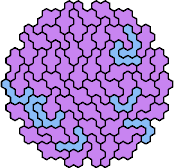
| 
| 
|
| 5JR | 5JU | 5JY | 5JZ | 5KL |

| 
| 
| 
| 
|
| 5KN | 5KP | 5KQ | 5KR | 5KS |

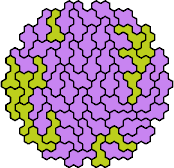
| 
| 
| 
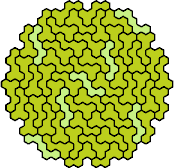
| 
|
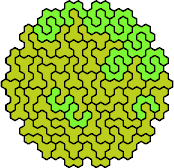
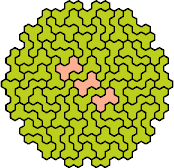
| 5KT | 5KU | 5KV | 5KW | 5KX |

| 
| 
| 
| 
|
| 5KY | 5KZ | 5LN | 5LP | 5LQ |

| 
| 
| 
| 
|
| 5LR | 5LS | 5LU | 5LV | 5LW |

| 
| 
| 
| 
|
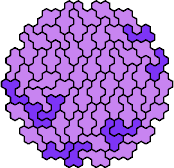
| 5LY | 5LZ | 5NP | 5NQ | 5NR |

| 
| 
| 
| 
|
| 5NS | 5NT | 5NU | 5NV | 5NW |

| 
| 
| 
| 
|
| 5NX | 5NY | 5NZ | 5PQ | 5PR |
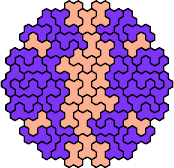
| 
| 
| 
| 
|
| 5PS | 5PT | 5PU | 5PV | 5PW |
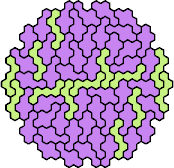
| 
| 
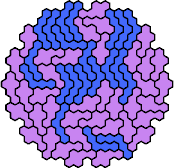
| 
| 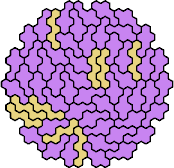
|
| 5PX | 5PY | 5PZ | 5QR | 5QU |
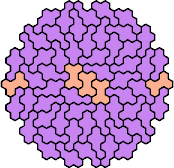
| 
| 
| 
| 
|
| 5QV | 5QW | 5QY | 5QZ | 5RS |

| 
| 
| 
| 
|
| 5RT | 5RU | 5RV | 5RW | 5RX |

| 
| 
| 
| 
|
| 5RY | 5RZ | 5SV | 5SY | 5SZ |

| 
| 
| 
| 
|
| 5TY | 5TZ | 5UY | 5UZ | 5VY |
| 
| 
| 
| 
|
| 5VZ | 5WY | 5WZ | 5XY | 5XZ |

| 
| 
| 
| 
|
| 5YZ | ||||

|
Last revised 2024-06-24.