Pentahex Pair Oddities

• Introduction
• Basic Solutions
• Lesser Symmetries
• Holeless Variants

Introduction

See also Pentomino Pair Oddities and Hexiamond Pair Oddities.

Helmut Postl improved on some of my solutions.

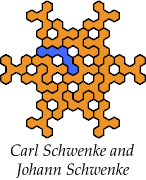
Carl and Johann Schwenke improved many of my solutions and solved cases that were previously unsolved.

Chronology of Solutions

Basic Solutions

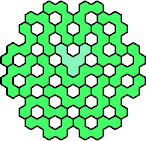
5AC 59	5AD 11	5AE 17	5AF 17	5AH 17
5AI 23	5AJ 17	5AK 23	5AL 17	5AN 11
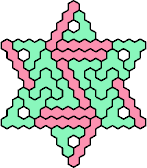
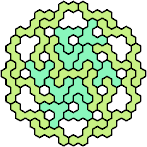
5AP 11	5AQ 17	5AR 17	5AS 29	5AT 53
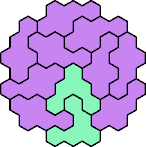
5AU 29	5AV 23	5AW 17	5AX 29	5AY 17
5AZ 23	5CD 11	5CE 23	5CF 17	5CH 23
5CI 47		5CJ 29	5CK 17	5CL 17
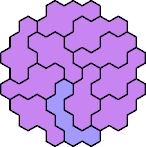
		5CN 17	5CP 11	5CQ 35
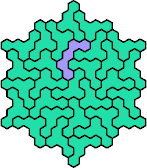
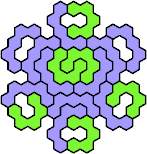
5CR 29	5CS 23	5CT —	5CU 17	5CV 29
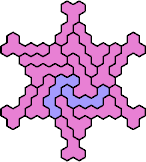
5CW 35	5CX 53	5CY 17	5CZ 17	5DE 11
5DF 11	5DH 11	5DI 11	5DJ 11	5DK 11
5DL 11	5DN 11	5DP 11	5DQ 11	5DR 11
5DS 11	5DT 11	5DU 11	5DV 11	5DW 11
5DX 11	5DY 11	5DZ 11	5EF 17	5EH 23
5EI 17	5EJ 23	5EK 17	5EL 17	5EN 17
5EP 11	5EQ 23	5ER 17	5ES 17	5ET 41
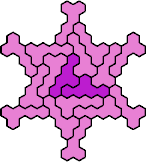
5EU 29	5EV 29	5EW 29	5EX 17	5EY 17
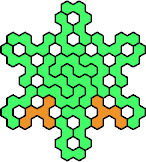
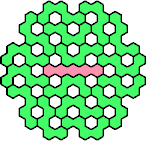
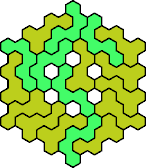
5EZ 17	5FH 17	5FI 17	5FJ 11	5FK 17
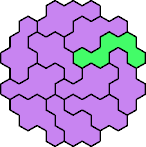
5FL 17	5FN 17	5FP 11	5FQ 17	5FR 17
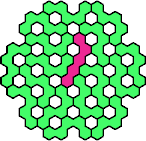
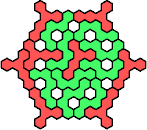
5FS 17	5FT 17	5FU 23	5FV 17	5FW 17
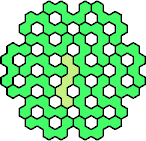
5FX 17	5FY 17	5FZ 17	5HI 5	5HJ 17
5HK 11	5HL 17	5HN 11	5HP 11	5HQ 17
5HR 17	5HS 11	5HT 17	5HU 23	5HV 17
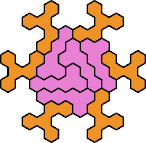
5HW 23	5HX 11	5HY 11	5HZ 17	5IJ 17
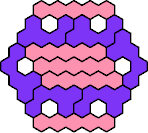
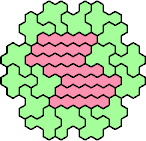
5IK 23	5IL 11	5IN 11	5IP 11	5IQ 23
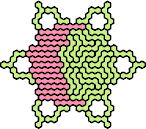
5IR 17	5IS 47	5IT 41	5IU 23	5IV 35
5IW 29	5IX 65	5IY 11	5IZ 17	5JK 17
5JL 17	5JN 11	5JP 11	5JQ 17	5JR 11
5JS 17	5JT 23	5JU 23	5JV 17	5JW 29
5JX 17	5JY 11	5JZ 17	5KL 17	5KN 11
5KP 11	5KQ 11	5KR 11	5KS 11	5KT 23
5KU 11	5KV 23	5KW 11	5KX 11	5KY 11
5KZ 11	5LN 11	5LP 11	5LQ 17	5LR 17
5LS 11	5LT 23	5LU 17	5LV 23	5LW 23
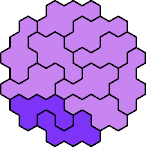
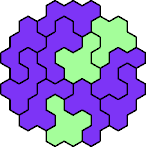
5LX 23	5LY 11	5LZ 11	5NP 11	5NQ 11
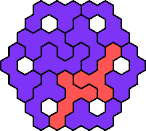
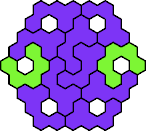
5NR 11	5NS 17	5NT 11	5NU 11	5NV 11
5NW 17	5NX 17	5NY 11	5NZ 17	5PQ 11
5PR 11	5PS 11	5PT 11	5PU 11	5PV 11
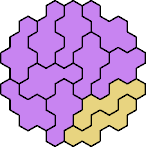
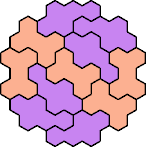
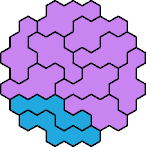
5PW 11	5PX 11	5PY 11	5PZ 11	5QR 17
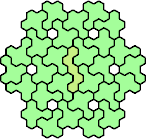
5QS 29	5QT 23	5QU 11	5QV 23	5QW 5
5QX 23	5QY 17	5QZ 11	5RS 23	5RT 17
5RU 17	5RV 17	5RW 17	5RX 17	5RY 11
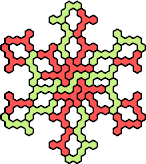
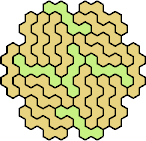
5RZ 17	5ST 29	5SU 23	5SV 23	5SW 23
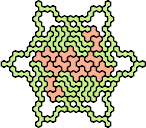
5SX 53	5SY 11	5SZ 23	5TU 35	5TV 23
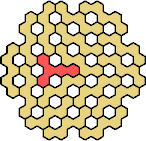
5TW 17	5TX 29	5TY 17	5TZ 23	5UV 23
5UW 17	5UX 11	5UY 17	5UZ 23	5VW 29
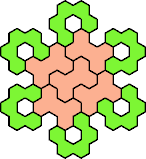
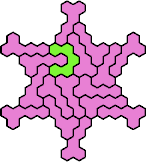
5VX 29	5VY 17	5VZ 17	5WX 11	5WY 17
5WZ 17	5XY 11	5XZ 11	5YZ 11

Lesser Symmetries

Holeless Variants

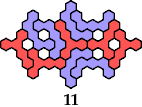
5AC —	5AE 23	5AF 29	5AI 53	5AS 53
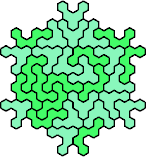
5AT 59	5AU 77	5AV 29	5AX 53	5CE —
5CF 41	5CH 29	5CI —	5CJ 35	5CN 23
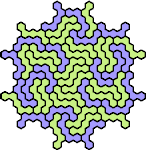
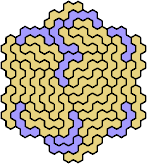
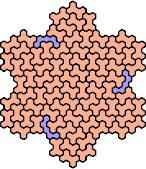
5CQ —	5CS 47	5CU 59	5CW 41	5CX 83
5EF 29	5EI 83	5EJ 29	5EK 29	5ES 65
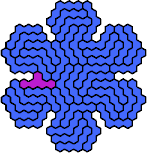
5ET —	5EU 47	5EV 41	5EX 53	5FH 23
5FI 59	5FJ 35	5FK 23	5FL 23	5FS 29
5FT 35	5FU 59	5FV 41	5FX 41	5HI 11
5HJ 29	5HL 23	5HT 29	5HV 29	5HW 29
5IK 29	5IN 23	5IS 71	5IT —	5IU —
5IW 41	5IX —	5IY 17	5JQ 29	5JT 47
5JU 47	5JV 23	5JW 41	5KT 29	5LU 23
5NT 29	5NU 23	5NV 17	5QR 23	5QS 35
5QU 23	5QW 17	5RS 29	5RT 23	5RU 23
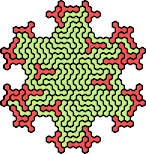
5RY 17	5ST 83	5SU 41	5SV 29	5SX 59
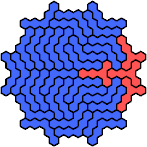
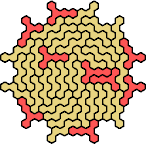
5SY 17	5SZ 29	5TU 53	5TV 35	5TW 41
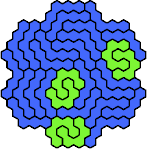
5TX 83	5UV 29	5UW 41	5UX —	5VW 41
5XY 17

Last revised 2024-10-07.