Uno n-omino è una forma ha fatto la pace di n quadrati ha congiunguto da completo orli. Potrebbe considerarlo anche essere una collezione di taglio delle quadrate da una griglia quadrata. Nella diagramma sotto le tre figure sul sinistro è polyimini ma i due sul giusto non è
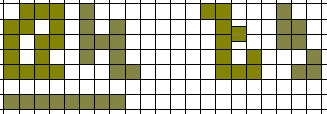
Per un elenco di numeri di polymini fino a ordine 28 vede polyomino enumeration da Tomás Oliveira e Silva, The Mathematics of Polyominoes da Kevin L. Gong o Klarner's Lattice Animal Constant. Per diagrammi di polymini fino a taglia 12 vede List of polyominoes of order 4..12 da Ambros Marzetta. C'è anche alcune informazioni in Polyominoes, etc. da Beeler, M., Gosper, R.W., e Schroeppel, R, Polyominoes da Slavik Jablan, Enumeration of Remarkable Families of Polyominoes da Dominique Gouyou-Beauchamps, Polypleura e Description des polyominos da Lawrence Detlor (in francese).
Sperimentare con disegno polimini prova Phil's Polyomino Maker
Per informazioni più tecniche sul problema del conta veda A Procedure for Improving the Upper Bound for the Number of n-ominoes e A Finite Basis Theorem Revisited.
![]()
Ci sono cinque tetramini (vede sopra). Svortunatamente, benchè coprono un'area totale di 20 quadra non possono essere congiunguti insieme a formare un rettangolo. Se usiamo il colorante dei pezzi mostra sopra allora i primi quattri pezzi coprono due quadrate biance e due nere ma lo scorso deve coprire tre di uno colore ed uno dell'altro. Da qualsiasi rettangolo con area 20 avrebbe 10 quadrate nere e 10 bianche sotto un tale colorante nessuno tale rettangolo può essere fatto. Il tetramini può essere congiunguto formare alcune forme interessanti comunque ed il diagramma sotto drammi come possono andare bene in un 3x7 rettangolo con una quadrata omettuta. Avviso quello di questi modelli erano colorate nero e bianco avrebbero 11 quadra di un colore e 9 dell'altro.

La dodici coperta dei pentamini un'area di 60 quadra. Questa area può essere fatta la pace con rettangoli 2x30, 3x20, 4x15, 5x12 e 6x10. Da almeno uno del pentamini è di lunghezza 3 in due direzione il 2x30 non è possibile ma tutti gli altri sono (vede sotto).
Per elenchi di soluzioni con diagrammi vada a Pentomino Relationships da Adrian Smith, Pentominos da Lars Kindermann, Introduction to Polyominoes da Eric Wassenaar o All Pentomino Solutions.
Per solamente il 6x10 rettangolo vede anche Equivalence Classes Among Pentomino Tilings of the 6x10 Rectangle da Wilfred J. Hansen.
Per un'animazione della costruzione di un 3x20 rettangolo vede Michelle Raymond's Homepage o per soluzioni animate di tutti rettangoli vede Pentominoes da Lars Kindermann.
Provare ripieno un 6 x 10 rettangolo va a Robert's Neat Math Page - Pentominoes
Puzzlecraft vende un CD con un gran numero di problemi del pentamini.
Altro luoghi con pentamini è
One sided pentomino rectangle The Know Madz Pentominoes Centre for Innovation in Mathematics Teaching Pentominoes Rashmi Bhat and Audrey Fletcher Gerard's Pentomino Page Het Pentomino-Doolhof (in Dutch) Livio Zucca's homepage Happy Pentominoes Anche Puzzle Fun da Rudolfo Kurchan ha competizioni regolari con pentamini .
C'è 35 examini. Svortunatamente, come col le tetramini, un dispari numero di questi ha un 4-2 colorante della scacchiera e così nessuno rettangolo può sia riempire con tutto 35.

Può vedere una costruzione delle octomini a Kadon Enterprises quale vende collezioni di pezzi.
David Bird ha fatto anche alcune costruzioni con gli octamini ed almeno uno con enneamini. (Questi disegni sia approvvigionato da Mike Reid)
Collegamenti
|
Hello Polyomino ha un buon elenco di altro collegamenti |
|
Polyomino
Problems and Variations of a Theme da Jan Kok
|
|
Medians
of polyominoes: a property for the reconstruction da Alberto Del
Lungo
|
| Aad van de Wetering Polyominoes (in olandese) |
| Pentomino Fuzion Puzzles |
| Geometry Junkyard David Eppstein |
| World Game Review da Michael Keller ha alcune informazioni su poliformi. |
| Miroslav Vicher's Puzzles Pages |
| Pentomino hungarIQa ha una variazione interessante sulle pentaomini |
| Ali Muniz ha una pagina di problemi della copertura dei polimini |
| Puzzles da Martin Watson |
| Welcome to Polyominoes da Kevin Gong |