 |
 |
 |
 |
 |

NOTE: pattern alternates between composite and prime (until x=10). Too bad !
A. H. Beiler, Recreations in the Theory of Numbers p. 85
![]()
191 & 383
39493939493
& 78987878987If P is greater than 2 and is a prime, than if 2P+1 is also prime, P is known as a Sophie Germaine prime. There are many such primes but only 71 pairs with three to eleven digits if both primes are palindromic. Above are the lowest and the highest such pairs.
If Q (2P+1) is itself a Sophie Germaine prime there are a total of 19 such triplets where each prime is palindromic. They range in size from 23 digits long to 39 digits long The smallest such triplet follows:
19091918181818181919091, 38183836363636363838183, 76367672727272727676367
Harvey Dubner, JRM 26:1, 1994, pp38-41t
![]()
If we let A=1, B=2, C=3, etc than
P+A+L+I+N+D+R+O+M+E+S + A+R+E + F+U+N =
19115551
(the smallest palindromic prime producing another in this way) when written in wordsF+I+F+T+E+E+N + T+H+O+U+S+A+N+D +
F+I+V+E + H+U+N+D+R+E+D + F+I+F+T+Y + O+N+E = 383
This courtesy of G. L. Honaker, Jr. (See Prime Queen Problem below)
![]()
30103 is the only known multi-digit palindromic prime found by averaging the divisors of a composite number.
30103
= (1 + 5 + 173 + 865 + 29929 + 149645)/630103 = average of divisors of 149645
30103 = average of divisors of 179574
It was found by Jud McCranie and G. L. Honaker, Jr. in July/98.
See Carlos Rivera’s Prime Puzzles & Problems
Fermat & Mersenne Numbers
Fermat numbers , when expressed in binary, have all zeros with a one at each end. Mersenne
numbers have all ones.
Both the decimal and binary numbers are palindromes (read the same backwards as
forewards).
![]()
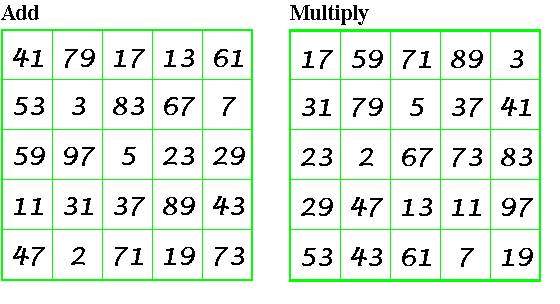
These two squares each contain the 25 primes that are less then 100.
Add
The maximum sum of any row, column or diagonal is 213
The minimum sum is 211
The difference (which is the minimum possible) is 2
Multiply
The maximum product of any line, column or diagonal is 19013871
The minimum product is 18489527
The difference which is also the minimum possible .is 524344
JRM vol. 26: 4, 1994 ,p. 308,309 Prob. 2094 proposed by R. M. Kurchan, solution by M. Reed
![]()
|
Proposed by G. L. Honaker, Jr. on Nov. 15, 1998.
|
Find the greatest number of prime squares that a queen
can attack if placed on an n by n knight's tour
solution. For the purpose of this problem, when considering if the queen is
attacking a particular square, assume the intervening squares are vacant.
|
By early December, 1998, Mike Keith had found these two solutions.. The order-8 has all of the 18 prime numbers less then 64 under attack by the queen placed on number 35. The order-5 square is also perfect because the queen is attacking all 9 of the primes when placed on the number 25.
In fact, Mr. Keith found perfect solutions also for order-6 and order-7 squares. It is impossible to have a knight tour solution for orders 2, 3 , or 4 and Mr. Keith conjectures that it is impossible to have a perfect solution for boards of order-9 or greater.
Can you find any other perfect solutions to this problem?
Addendum:
| On April 1, 2004, I received an email from Jacques Tramu.
He enclosed a solution he had found for the perfect order 9 square of this
type. All 22 primes in the number range of 1 to 81 are attacked by the
queen. He shows the solution at http://mapage.noos.fr/echolalie/q9.htm A few days later I also received a notice of this solution from G. L. Honaker, Jr., the originator of this problem. |
|
Addendum2:
April 12, 2004. 5 minutes after uploading the previous addendum, I checked my
email. Another update from G.L.
Jacques has just published a perfect order 10! See it at his link shown above.
See Mike Keith's information on this problem at http://users.aol.com/s6sj7gt/primeq.htm
|
272 |
213 |
214 |
215 |
216 |
217 |
218 |
219 |
220 |
221 |
222 |
223 |
224 |
225 |
226 |
227 |
|
271 |
212 |
161 |
162 |
163 |
164 |
165 |
166 |
167 |
168 |
169 |
170 |
171 |
172 |
173 |
228 |
|
270 |
211 |
160 |
117 |
118 |
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 |
127 |
174 |
229 |
|
269 |
210 |
159 |
116 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
128 |
175 |
230 |
|
268 |
209 |
158 |
115 |
80 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
90 |
129 |
176 |
231 |
|
267 |
208 |
157 |
114 |
79 |
52 |
33 |
34 |
35 |
36 |
37 |
60 |
91 |
130 |
177 |
232 |
|
266 |
207 |
156 |
113 |
78 |
51 |
32 |
21 |
22 |
23 |
38 |
61 |
92 |
131 |
178 |
233 |
|
265 |
206 |
155 |
112 |
77 |
50 |
31 |
20 |
17 |
24 |
39 |
62 |
93 |
132 |
179 |
234 |
|
264 |
205 |
154 |
111 |
76 |
49 |
30 |
19 |
18 |
25 |
40 |
63 |
94 |
133 |
180 |
235 |
|
263 |
204 |
153 |
110 |
75 |
48 |
29 |
28 |
27 |
26 |
41 |
64 |
95 |
134 |
181 |
236 |
|
262 |
203 |
152 |
109 |
74 |
47 |
46 |
45 |
44 |
43 |
42 |
65 |
96 |
135 |
182 |
237 |
|
261 |
202 |
151 |
108 |
73 |
72 |
71 |
70 |
69 |
68 |
67 |
66 |
97 |
136 |
183 |
238 |
|
260 |
201 |
150 |
107 |
106 |
105 |
104 |
103 |
102 |
101 |
100 |
99 |
98 |
137 |
184 |
239 |
|
259 |
200 |
149 |
148 |
147 |
146 |
145 |
144 |
143 |
142 |
141 |
140 |
139 |
138 |
185 |
240 |
|
258 |
199 |
198 |
197 |
196 |
195 |
194 |
193 |
192 |
191 |
190 |
189 |
188 |
187 |
186 |
241 |
|
257 |
256 |
255 |
254 |
253 |
252 |
251 |
250 |
249 |
248 |
247 |
246 |
245 |
244 |
243 |
242 |
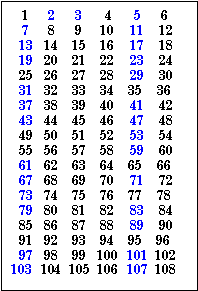
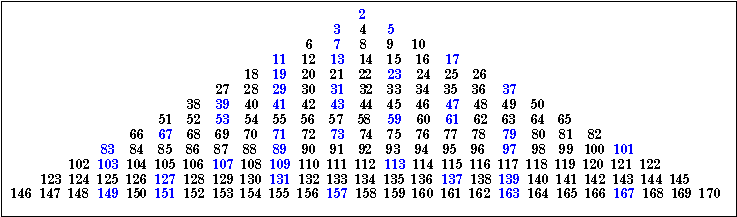
| Probably everyone has heard the story about how Stanislaw M. Ulam discovered this
pattern while sitting in a scientific meeting listening to what he described as a
"long and boring paper." My first experience with his prime spiral was in the
mid 70’s when I programmed it on my Apple II computer using Euler’s formula
x2 + x + 41. The graphics screen had a resolution
of 40 x 40, and I can remember the thrill I received as I watched the screen slowly (but
in those days I thought it was fast) fill up with a solid diagonal of 40 primes from one
corner to the other. A good explanation of this pattern is in M. Gardner, Sixth Book of Mathematical Games, Scribner’s, 1971 The triangle plot and the linear plot both show the primes in neat columns. The linear plot with six numbers per line illustrates how all primes are 6n - 1 or 6n + 1 (except for 2 and 3). |
 |
![]()
| Dr. Ellerstein pointed out that Ulam's
spiral also has the diagonal of squares with the other diagonal consisting
of pronics (as does his). Here I show Ulam's spiral starting at 0. But instead of showing the primes, I show the diagonal of squares and the diagonal of pronics. Pronics are the product of two adjacent numbers. |
72 71
70 69 68 67 66 65
64 99 73 42 41 40 39 38 37 36 63 98 74 43 20 19 18 17 16 35 62 97 75 44 21 06 05 04 15 34 61 96 76 45 22 07 00 03 14 33 60 95 77 46 23 08 01 02 13 32 29 94 78 47 24 09 10 11 12 31 58 93 79 48 25 26 27 28 29 30 57 92 80 49 50 51 52 53 54 55 56 91 81 82 83 84 85 86 87 88 89 90 |
![]()
A prime spiral arranged as a circle is thoroughly discussed and illustrated at Rom Sacks http://www.numberspiral.com/

Is there at least 1 prime adjacent to each multiple of 6?
Addendum Nov. 5, 2002
Dr. Ellerstein (see above section) advised me that the
answer to the above question is NO!
The first exception is for n = 20
The 3 adjacent numbers are 119, 120, and 121 (119 = 7 x 17 and
also 122 - 52, 120 = 6n, and 121 = 112
![]()
1193, 1201, 1213, 1217,1223,1229,1231, 1237, 1249, 1259
A sequence of ten consecutive primes. Each one of these primes is still a prime when the order or the digits is reversed.
This sequence was discovered by Carlos Rivera, and is registered by him in Sloane’s Integer Sequences as A040104.
![]()
5882353 = 5882 + 23532
This is the only prime number I know with this property. Are there other primes like this?
See examples of composite numbers with this or similar properties at my Narcissistic Numbers page.
![]()
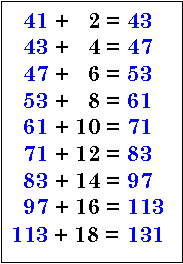
Does this pattern continue producing primes forever?
Addendum Nov. 19, 2002
No. See Ulam's Spirol (above). Aguydude pointed this out to me.
![]()
8 consecutive primes
11 13 17 19 23 29 31 37These eight consecutive primes have the form k, k + 2, k + 6, k + 8, k + 12, k + 18, k + 20, k + 26.
The next such series starts with the prime 15,760,091 and there are 6 more such series below 1,000,000,000
Martin Gardner, The Last Recreations, p204
![]()
This pattern has 8 rows of 11 consecutive primes summing to a prime number.
Each row stars with the second prime in the row above it.
To save space, all primes (except the totals) are of the following form: 352XXXX

This pattern was found by Carlos Rivera and appeared on Prime Puzzles & Problems in Aug./98.
Since then, Jud McCranie has found many more of these patterns. See his pattern with 9
rows of 97 primes each at
Carlos Rivera’s WWW site .
![]()
To save space, all primes (except the totals) are of the following form: 12606XXXX

There are three more lines to this pattern. The first and last primes in the last line are 126064739 and 126065033. The sum of this line is 2143103093.
This pattern was found by Carlos Rivera and appeared on his Prime Puzzles & Problems in Aug./98.
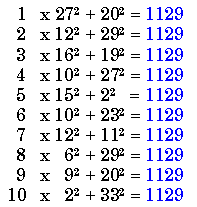 |
Primes 1009 and 1201 have the same property. The smaller prime numbers 241,409, 601, and 769 almost have this property. In each case the only n for which there is no solution is n = 7. Charles Ashbacher, JRM 24:3, 1992, pp202 Carlos Rivera (see his Prime Puzzles &
Problems) sent me on Aug. 8/98, the solution
below for n equals the first ten even numbers. |
![]()
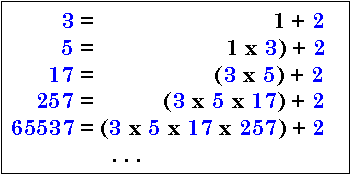 |
Every Fermat number is the product of all previous |

This is spelled out by Euclid in his Proposition 36 of Book IX of the Elements.
December, 2005: V.V. Raman reports "that every perfect number is 1 (mod 9)?"
See an excellent paper on Perfect numbers at
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Perfectnumbers.html
![]()
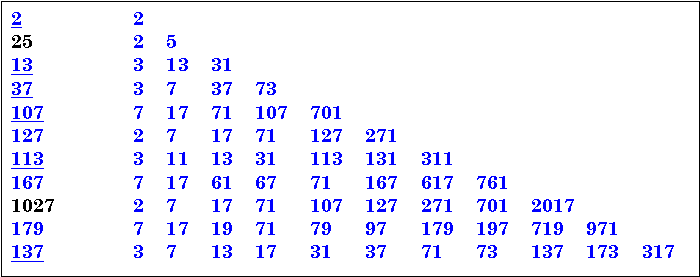
In each case, the number in the left column is the lowest number that includes this
many primes.
The underlined numbers are Primeval Primes.
See more on Primeval Primes at Mike Keith’s page at http:users.//aol.com/s6sj7gt/primeval.htm
![]()
![]()
![]() (57)
= 24 and 5757 - 24 is prime
(57)
= 24 and 5757 - 24 is prime
57 x 225 - 1 is prime
57 + (100 x 2n ) are primes for n = -1, 0, 1, 2, 3, 4 & 5
I modestly refer to this as "Heinz's number".
See more curios at http://primes.utm.edu/curios/
![]()
Reginald Brooks has recently completed an extensive work on what he refers to as Butterfly Primes.
I was made aware of this by several emails from him, the most recent being March 2, 2006.
His site contains much information and many attractive multicolored tables.
This is a prime example of what I (and others) have often claimed, that
"mathematics is a study of the patterns of numbers!"
Reginald's papers (including other number pattern topics) may be viewed at
http://www.brooksdesign-cg.com/Code/Html/arthry2.htm
![]()
Please send me Feedback about my Web
site!
![]()
![]()

![]()
Last updated
June 19, 2007
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998, 2000 by Harvey D. Heinz