 |
 |
 |
 |
 |
Narcissus, according to Greek mythology, fell in love with his own image,
seen in a pool of water, and changed into the flower now called by his name.
Since this section deals with numbers "in love with themselves", narcissistic
numbers will be defined as those that are representable, in some way, by
mathematically manipulating the digits of the numbers themselves.
Definition by Joseph S. Madachy, Mathematics on Vacation, Thomas
Nelson & Sons Ltd. 1966
He has lots of material on narcissistic numbers on p 163 to 175 of this book.
![]()
| 4624 = 44+46+42+441033 = 81+80+83+83 | Note that the powers match the digits of the number. |
3909511 = 53+59+50+59+55+51+51 13177388 = 71+73+71+77+77+73+78+78 52135640 = 195+192+191+193+195+196+194+190 |
To the left are some of those sent to me by Patrick de Geest in Dec.,1998, along with the name suggestion. |
![]()
3435 = 3
3 + 44 + 33 +55438579088 = 4
4 + 33 + 88 +55 + 77 + 99 + 00 + 88 + 88These are called Perfect Digit-to-Digit Invariants or PDDI's
for short. (See PDI, PPDI and RDI at the bottom of this page.)
The only two integers in the decimal number system with this property (plus the trivial 0
& 1).
D. Morrow ran a search up to 109 with no additional finds accept the trivial
adding of zeros to the above 2 numbers.
Note that here 00 is considered equal to 0. Normally 00 is
considered equal to 1 (see above 1033 where 80 = 1).
Curious and Interesting Numbers p.190 and D. Morrow JRM 27:1, 1995 p 9
and JRM 27:3, 1995, p205-207
Reverse of Above
48625 = 4
5 + 82 + 66 +28 + 54397612 = 3
2 + 91 + 76 + 67 + 19 + 23The powers are the same as the digits, but in reverse order.
Thanks to Patrick De Geest for these two numbers
![]()
127 = -1 + 2
7 3125 = (31 + 2)5759375 = (7 - 5 + 9 - 3 + 7)5
![]()
Ascending & Descending Powers
1676 = 1
1 + 62 + 73 + 641676 = 1
5 + 64 + 73 + 62NOTE: the order of the powers.
![]()
43 = 42 + 33 63 = 62 + 33
![]()
89 = 81 + 92
518 = 51 + 12 + 83 598 = 51 + 92 + 83
1306 = 11 + 32 + 03 + 64 2427 = 21 + 42 + 23 + 74
2646798 = 21
+ 62 +43 + 64 + 75 + 96 + 87
Thanks to Patrick De Geest for these last two numbers
![]()
343 = (3 + 4)
3 3456 = 3! x 4/5 x 6!355 = 3 x 5
! - 5 4096 = (4 + 0 x 9)6715 = (7 - 1)
! - 5 5161 = 5! + (1 + 6)! + 1729 = (7 + 2)Ö
9 6859 = (6 + 8 + 5)Ö 9Wild Narcissistic Numbers
24739 = 2
4 + 7! + 3923328 = 2 x 3
3! x 2 x 8For more Wild Narcissistic numbers see Mike Keith's home page at http://users.aol.com/s6sj7gt/mikewild.htm
![]()
In 1917, H. E. Dudeney published a book of mathematical recreations called Amusements
in Mathematics. Amusement # 115 tells of a printer when required to set the type for
number 25•92, mistakenly set it as 2592 (the dot was meant to
indicate multiplication). However, upon proofreading the number, it was found to be
correct as written.
The other numbers presented here were found by D. L. Vanderpool of Pennsylvania and
presented in J. S. Madachy's Mathematics on Vacation, 1966, 17-147099-0.
2
5·92 = 2592Here are some with fractions
1129 1/3 = 11
2·9 1/3 2124 9/11 = 212·4 9/11Some lead to infinite series of errors
34425 = 34·425
312325 = 312·325
344250 = 34·4250
3123250 = 312·3250
3442500 = 34·42500
31232500 = 312·32500
etc
etc
![]()
81
=
(8+1)2
=
92
512
=
(5+1+2)3
=
83
4913
=
(4+9+1+3)3
=
173
17576
=
(1+7+5+7+6)3
=
263
234256
=
(2+3+4+2+5+6)4
= 224
1679616
=
(1+6+7+9+6+1+6)4
=
364
17210368
=
(1+7+2+1+0+3+6+8)5
=
285
205962976
=
(2+0+5+9+6+2+9+7+6)5
= 465
8303765625
= (8+3+0+3+7+6+5+6+2+5)6
= 456
24794911296 =
(2+4+7+9+4+9+1+1+2+9+6)6
= 546
271818611107 =
(2+7+1+8+1+8+6+1+1+1+0+7)7 = 437
6722988818432 =
(6+7+2+2+9+8+8+8+1+8+4+3+2)7 = 687
72301961339136 = (7+2+3+0+1+9+6+1+3+3+9+1+3+6)8 = 548
248155780267521 = (2+4+8+1+5+5+7+8+0+2+6+7+5+2+1)8 = 638
Where a digital invariant was defined as a number equal to the sum of the nth powers of its digits, this category has numbers equal to a power of the sums of their digits.
J.S.Madachy, Mathematics On Vacation p.167 - 170 presents an algorithm that results in a relatively small search field for numbers of this type. It turns out there are 432 such numbers in the range to P101 , the largest, having 320 digits with a digit sum of 1468, is 1468101.
A related number
1,180,591,620,717,411,303,424 = 2
70
and the sum of the digits in 270
equals 70.

![]()
| 12 33 = 122 + 332 990 100 = 9902 + 1002 9412 2353 = 94122 + 23532 74160 43776 = 741602 + 437762 116788 321168 = 1167882 + 3211682 |
Each number is equal to the sum of the squares of its two halves. 88 33 = 882 + 332 Is this the only other 4 digit number with this property? |
|
4 8 = 82 - 42 34 68 = 682 - 342 416 768 = 7682 - 4162 3334 6668 = 66682 - 33342 |
Each number is equal to the difference of the squares of its two halves. Does a pattern like this exist for sum of the squares of its two halves? |
|
22 18 59 = 223 + 183 + 593 166 500 333 = 1663 + 5003 + 3333 |
Each number is equal to the sum of the cubes of its three thirds. |
![]()
3869 = 622 + 052 and 6205 = 382 + 692
5965 = 772 + 062 and 7706 = 592 + 652
Each number of the pair is equal to the sum of the squares of the two halves of the other number.
And somewhat similar
13+33+63 = 244 and 23+43+43 =
136
![]()
298 = (22 + 92 + 82) + (22 + 92 + 82)
336 = (31 + 31 + 61) + (32 + 32 + 62) + (33 + 33 + 63)
444 = (41 + 41 + 41) + (42 + 42 + 42) + (43 + 43 + 43) + (43 + 43 + 43)
Above are examples of power-sum numbers. The number 336 is a subclass called proper because the groups of exponents are all distinct.
M. Keith, Journal of Recreational Mathematics 18:4 1985-86, p 275
![]()
666 = (61 + 61 + 61) + (63 + 63 + 63)
Also 666 = 16 - 26 + 36
Unique Factorials (Factorians)
1 = 1!
2 = 2!
145 = 1! + 4! + 5!
40585 = 4! + 0! + 5! + 8! + 5!
These are the only integers with this property.
Remember factorial 0 is 1 by definition.
Clifford Pickover calls these numbers Factorians. See his Keys to Infinity, p.169-171.
![]()
0! * 1! = 1!
1! * 2! = 2!
6! * 7! = 10!
1! * 3! * 5! = 6!
1! * 3! * 5! * 7! = 10!
Are these the only examples of factorials that are the products of factorials in arithmetic sequence or progression?
![]()
4! + 1 = 52 5! + 1 = 112 7! + 1 = 712
Are there more of these numbers?
Clifford Pickover, Keys to Infinity, p. 170
![]()
The only solution for sum of subfactorials of digits ?
148,349 = !1 + !4 + !8 + !3 + !4 + !9
The exclamation point in front of the number indicates it is a sub-factorial.
Subfactorials are defined as follows:
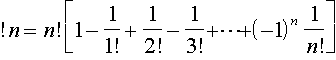
The subfactorials of the digits are : !0 = 0, !1 = 0, !2 = 1, !3 = 2, !4 = 9, !5 = 44, !6 = 265, !7 = 1854, !8 = 14833, !9 = 133496.
J. S. Madachy, Mathematics on Vacation, p. 167
![]()
4150 = 45 + 15 + 55 + 05
4151 = 45 + 15 + 55 + 15
194979 = 15 + 95 + 45 + 95 + 75 + 95
14459929 = 17 + 47 + 47 + 57 + 97 + 97 + 27 + 97
A PDI is a number equal to the sum of a power of
its digits when the power is not equal to the length of the number.
A 41 digit PDI is
36,428,594,490,313,158,783,584,452,532,870,892,261,556.
It is equal to the sum of each of its digits raised to the 42nd power. L. E. Deimel, Jr and M. T. Jones, JRM,14:4,
1981-82 p284

![]()
153 = 13
+ 53 + 33
1634 = 14 + 64 +
34 + 44
54748 = 55 + 45 +
75 + 45 + 85
548834 = 56 + 46 +
86 + 86 + 36
+ 46
1741725 = 17 + 77 +
47 + 17 + 77
+ 27 + 57
24678050 = 28 + 48 +
68 + 78 + 88
+ 08 +58 +
08
146511208 = 19 + 49 +
69 + 59 + 19
+ 19 + 29 +
09 + 89
4679307774 = 410 + 610
+ 710 + 910 + 310 + 010
+ 710 + 710 + 710 + 410
82693916578 = 811 + 211
+ 611 + 911 + 311 + 911
+ 111 + 611 + 511 + 711
+ 811
The above numbers are called Pluperfect Digital
Invariants or PPDIs. They are also called Armstrong Numbers. In each case, the power
corresponds to the number of digits. There are no PPDIs for numbers of 2, 12 or 13 digits.
The number shown for 11 digits is one of eight such numbers. Largest possible PPDI has 39
digits. It is 115,132,219,018,763992,565,095,597,973,971,522,401. It is equal to the sum of the 39th power of its
digits.
NOTE that all single digit numbers, in all bases, are PPDIs. The other comments above
refer to base 10 PPDIs.
See L. Deimel, Jr. & M. Jones, Finding Pluperfect Digital Invariants, JRM vol. 14:2, 1981-82, p 87-107 for a list of PPDI's in number bases 2 to 10, in base ten all 88 PPDI's to order-39. Also 6 references.
![]()
Each number of each of the following two series is known as a Recurring Digital Invariant or RDI.
Here is an order three RDI, 55, with two intermediate numbers before 55 appears again. The order four RDI, 1138, has six intermediate numbers before 1138 reappears. Notice that RDI’s are not necessarily Armstrong numbers i.e. the power is not necessarily the same as the length of the number. RDI’s, PDI's and PPDI’s are members of a larger class of numbers called narcissistic. A narcissistic number is defined as one that may be represented by some manipulation of its digits.
|
55 : 53 + 53 = 250 250 : 23 + 53 + 03 = 133 133 : 13 + 33 + 33 = 55 |
This is one of four RDI cycles of order-3 They are: 136, 244 length 2 919, 1459 length 2 55, 250, 133 length 3 ( the one to the left) 160, 217, 352 length 3 The four PPDI's: 153, 370, 371, 407 may each be considered a cycle of length 1. |
| 1138 : 14 + 14 + 34 + 84 = 4179 4179 : 44 + 14 + 74 + 94 = 9219 9219 : 94 + 24 + 14 + 94 = 13139 13139 : 14 + 34 + 14 + 34 + 94 = 6725 6725 : 64 + 74 + 24 + 54 = 4338 4338 : 44 + 34 + 34 + 84 = 4514 4514 : 44 + 54 + 14 + 44 = 1138 |
There is one other order-4 RDI. It has a cycle length of two and consists of 2178 and 6514. Also the three order 4 PPDI's 1634, 8208, 9474 may be considered cycles of length one.
|
![]()
Example strings leading to each PPDI, PDI or RDI of order-3
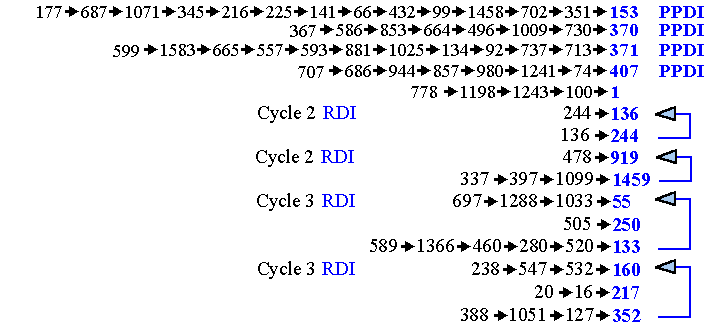
The sum of the cubes of the digits of each number forms the next number in the string until a cycle of length 1, 2 or 3 is reached..
| 72
= 49 42 + 92 = 97 92 + 72 = 130 12 + 32 + 02 = 10 12 + 02 = 1 |
1 is the first happy number. 7 is the second happy number. Iterating the process of summing the square
of the decimal digits of a number, you either reach ---the RDI cycle 4, 16, 37, 58, 89 145, 42, 20 and
back to 4 or
---you reach the number 1. |
Happy number 7 requires 5 iterations before it reaches
the number 1.
Happy number 356 requires 6 iterations before it reaches the number 1.
Happy number 78999 requires 7 iterations before it reaches the number 1.
The 10,012,125th Happy number is 71,406,333 and at this point 7 is still the maximum
iterations required.
Is 7 the maximum iterations required for any
number to evolve to 1 when each digit is squared and then summed?
Defined by R. K. Guy, Unsolved Problems in Number Theory, Springer-Verlag.
![]()
Summary: PDI, PPDI, RDI, & Happy numbers
![]()
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Ord-er # |
# of entry points |
# of RDI Cyc. |
What RDI Cycles |
Empty entry points |
# of PPDIs |
Entries to PPDIs |
maximum Iterations required |
# of starting numbers |
Root start # |
PDI's |
2 |
9 |
1 |
8 |
1 |
0 |
0 |
9 |
1 |
60 |
0 |
3 |
15 |
4 |
2, 2, 3, 3 |
0 |
4 |
761 |
13 |
3 |
177 |
0 |
4 |
12 |
2 |
2, 7 |
1 |
3 |
643 |
52 |
18 |
2899 |
0 |
5 |
102 |
9 |
2, 2, 4, 6, 10, 10, 12, 22, 28 |
9 |
3 |
727 |
56 |
90 |
15578 |
3 |
6 |
50 |
5 |
2, 3, 4, 10, 30 |
7 |
1 |
300 |
91 |
1380 |
127889 |
0 |
7 |
267 |
11 |
2, 2, 3, 6, 12, 14, 21, 27, 30, 56, 92 |
18 |
4 |
28140 |
106 |
360 |
3055588 |
1 |
8 |
182 |
3 |
3, 25, 154 |
3 |
maybe a |
bigger |
string? |
|||
9 |
299 |
13 |
2, 3, 3, 4, 8, 10, 10, 19, 24, 28, 30, 80, 93 |
4 |
||||||
10 |
234 |
6 |
2, 6, 7, 17, 81, 123 |
1 |
||||||
11 |
539 |
9 |
5, 7, 18, 20, 42, 48, 117, 118, 181 |
8 |
||||||
12 |
267 |
3 |
40, 94, 133 |
0 |
||||||
13 |
297 |
6 |
5, 8, 16, 22, 100, 146, |
0 |
1 | |||||
14 |
571 |
5 |
14, 15, 65, 96, 381 |
1 |
||||||
15 |
829 |
7 |
8, 12, 30, 46, 75, 216, 362 |
0 |
| 1 | Order of the PPDI i.e. the power each digit of the number is raised to. Also the length of each starting number. Each number in this range is evaluated except for the first one. 10, 100, 1000, etc always converges to the number 1. |
| 2 | These entry points are the value all
numbers in the range must eventually reduce to. They are PPDI's, PDI's, or members of an
RDI cycle. NOTE: I show only PDI's that have numbers in this range converging to them. There may be some PDI's in this range that are a result of numbers from other orders. All members of an RDI cycle are represented here although some may have NO numbers converging to them. |
| 3 | Number of individual RDI cycles. Cycles of length 1 (PPDI's and RDI's) are not shown here. |
| 4 | Lists the actual cycle lengths. There is often more then 1 cycle of the same length. |
| 5 | Some numbers in an RDI cycle may not have any numbers reducing to them, i.e this is NOT an entry point to the cycle. |
| 6 | Actual number of PPDI's of this order. Each one is of course one number in the range, but other numbers may also reduce to it after several or many iterations. |
| 7 | Shows how many numbers reduce to the PPDI's. |
| 8 | The maximum iterations required of a number in the range before it becomes a PPDI, a PDI (or 1), or a member of an RDI cycle. |
| 9 | The number of starting numbers requiring the maximum iterations. |
| 10 | The starting number for maximum iterations. All numbers with permutations of these digits are also start numbers. |
| 11 | Number of PDI's. Each of these is reached eventually from some number in the range. The first number in every range (10, 100, 1000, etc) always generates the number one. This fact is not shown in this column. Only orders 2 and 3 have other numbers that converge to one. |
NOTE: Number of RDI cycles for orders 10 – 15 may not be accurate (I may have missed some). Can you add to this table?
I have a word document containing more detailed notes resulting from this investigation. Is is called PPDI.doc (236 kb) and may be downloaded from my download page.
![]()
Please send me Feedback about my Web site!
![]()
![]()

![]()
Last updated
October 14, 2009
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998, 2000 by Harvey D. Heinz