Quadrant Magic Squares

As with all my pages, I appreciate comments and constructive criticism.

CONTENTS

Introduction

Some magic squares of orders m equal to 4n + 1, have arrays of m cells appearing in each quadrant that sum to the magic constant.
If a magic square contains 4 of these arrays in the 4 quadrants, and if they are all the same type, I call it a quadrant-magic square.

Consider a magic square of order m = 4n + 1 (i.e. 5, 9, 13, 17, etc).
Divide it into 4 quadrants such that each quadrant consists of (m + 1)/2 times (m + 1)/2 cells
Each array consists of m -1 cells, plus the central cell of the quadrant.
The array is considered magic if the m cells sum to the magic constant for the square.

Quadrant Magic Arrays
The cells in the array must be arranged so that they are orthogonally and diagonally symmetrical. This condition reduces the number of possible magic arrays to a manageable number (at least for the smaller magic squares).
Note that the central row and the central column of the Quadrant Magic Square is common to two orthogonally adjacent quadrants. This means that if an array has cells in the outside row and column, these cells are shared with the adjacent quadrant.

The first 6 magic arrays were all discovered by Aale de Winkel in May, 1999. They are the cross, plus sign, diamond, small ring, large ring and thickcross. He named them respectively, crosmagic, plusmagic diammagic, sringmagic, lringmagic and tcrosmagic.
After I found some additional arrays, he decided to investigate the subject systematically.
It turns out there are 10 classes of arrays, determined by their degree of symmetry. Because of the very large number of magic arrays, we define a Quadrant Magic Square as using only the highest order one of  these, the fully symmetric one. This class we call 'Quadrant' or quadrant magic array.
Aale enumerated the Quadrant magic patterns for orders 5, 9, 13 and 17 and labeled them with index numbers prefixed with a 'p'. For order 13 there are 38 quadrant magic patterns, but a total of 262,596,783,764 patterns counting all 10 classes of magic arrays.
See his Special_Magic.html page for details and listings. (The link to his site appears at the bottom of this page.)

The first five of the above named arrays are fundamental.
They appear in all orders 4n + 1 (altered, of course, to contain the correct number of cells).
Because the 'p' numbers for these patterns vary from order to order, these names will be retained.
Here are the fundamental arrays for order-9, with the corresponding 'p' number.

Quadrant Magic Squares
Some quadrant magic squares may be converted to isomorphic-like magic stars. For order-5, they are isomorphic. For the other orders, they are only pseudo-isomorphic because they cannot use all the numbers contained in the quadrant magic square.

The only magic array that may be used to form an iso-like magic star for all orders 4n+1 is the plusmagic.
Additionally, the diammagic array can form iso-like magic stars for orders 8n – 3.
The reasons for this are discussed in the iso-like magic star section.

On this page, I will show examples of quadrant-magic squares, present known and suspected characteristics, and pose a number of questions for further study.
I will also present an example of the order-5 isomorphic magic star to show how the quadrant magic square arrays are used to create these stars.

As my first example, here is an order-17 pandiagonal magic square that I show as quadrant magic four different ways by illustrating a different array in each quadrant. However, each array actually appears in all four quadrants.
As well as the 17 rows and columns, and the 34 diagonals, each of these arrays sum to the magic constant of 2465.

With the lringmagic arrays, there are five numbers common to each of two orthogonal arrays.
This is LP (14, 1, 0)(1, 14, 0).

I will discuss the characteristics of these arrays and quadrant magic squares in more detail as I introduce the different orders.

Suffice to say that in order to qualify as a quadrant magic square:

1. The square must be magic in the ordinary sense i.e. all rows, columns and the two main diagonals must be magic.
2. The magic square may be of any type i.e. normal, pandiagonal, associated, inlaid, etc.
3. All four quadrants of the square must contain the same magic array of m numbers, and it must be centered around the central number of the quadrant.
4. The array mentioned in statement 3 must be quadrant magic i.e. it must be fully symmetrical.
5. Statement three requires that the magic square be of order 4m + 1.

Notes:

1. Most magic squares will contain one (or more) magic arrays, but in only 1, 2, or 3 quadrants (or an array not centered in a quadrant).  Also, many magic squares will contain a pattern in all 4 quadrants that is not fully symmetrical.
   These squares are not quadrant magic squares!
2. In each order, the middle row of the magic square is common to both the top 2 quadrants and the bottom 2 quadrants. Likewise, the middle column is common to the pairs of quadrants on the left and right sides.

Order-5 quadrant magic squares

Quadrant diagrams
Order-5 essentially different pandiagonal ................... crosmagic, plusmagic
Order-5 1 of the 99 derivatives of above .................. crosmagic, plusmagic
Order-5 normal (not pandiagonal) ............................ no quadrant magic arrays
Order-5 normal (not pandiagonal) ............................ crosmagic, plusmagic
Order-5 normal associative ...................................... only 2 quadrant magic arrays
Order-5 normal associative ...................................... plusmagic, & 2 crosmagic
Order-5 pandiagonal associative .............................. plusmagic, & 2 crosmagic

3 7 14 16 25 11 20 23 2 9 22 4 6 15 18 10 13 17 24 1 19 21 5 8 12

This is one of the 99 pandiagonal derivations of the above square. It was obtained by transformation 1-3-5-2-4 applied to the rows and columns: then rows and columns interchanged with the diagonals; then another transformation 1-3-5-2-4 applied to the rows and columns. See Benson & Jacoby, New Recreations With Magic Squares, Dover, 1976, p.130. This one shows crosmagic arrays. However, both this and the previous magic square contain four of each of these two magic arrays.

17 13 5 6 24 9 25 11 2 18 21 4 8 20 12 3 16 22 14 10 15 7 19 23 1	This is an normal (not pandiagonal) magic square. It is not quadrant magic. There are no magic arrays.
1 7 19 13 25 18 15 21 2 9 22 4 8 20 11 10 16 12 24 3 14 23 5 6 17	This is a normal (not pandiagonal) magic square. This is a plusmagic quadrant magic square. Normal magic squares that are quadrant magic seem to be relatively rare.
12 1 20 9 23 21 15 4 18 7 10 24 13 2 16 19 8 22 11 5 3 17 6 25 14	This is a normal (not pandiagonal) associated magic square It is not quadrant magic because only two quadrants have a plusmagic array. It seems that there is always zero, two or four quadrants correct in order-5 magic squares.
9 2 25 18 11 3 21 19 12 10 22 20 13 6 4 16 14 7 5 23 15 8 1 24 17	This is a normal (not pandiagonal) associated magic square This is a plusmagic quadrant magic square. There are two crosmagic arrays, but only two (see them?), so this square is not a crosmagic quadrant magic square.
1 15 24 8 17 23 7 16 5 14 20 4 13 22 6 12 21 10 19 3 9 18 2 11 25	This is a pandiagonal associated crosmagic square The crosmagic array cannot be used to form an order-5 isomorphic star for 2 reasons There are two cells in common with the adjacent array instead of one. There are three cells on the diagonal instead of one. This square also is plusmagic (and diammagic), so an order-5 iso-like magic star may be made using these arrays.

Order-5 ...some conclusions and questions

Order-5 has only five magic arrays because of the small size of the quadrants, and only two of these are unique.
The plusmagic and diammagic arrays are identical, as are the crosmagic, sringmagic and lringmagic arrays.

All 36 essentially different pandiagonal magic squares are plusmagic on all 25 cells.
Does this apply to the 99 variations of each of these?

Only some regular order-5 are plusmagic.
Are any of these plusmagic for all 25 cells?

Are all of the nine pandiagonal associated magic squares plusmagic?

Are any of the regular associated magic squares plusmagic?

Iso-like magic Stars

A. Plusmagic 18 21 4 7 15 2 10 13 16 24 11 19 22 5 8 25 3 6 14 17 9 12 20 23 1	B. Crosmagic 18 21 4 7 15 2 10 13 16 24 11 19 22 5 8 25 3 6 14 17 9 12 20 23 1	The magic star shown below is isomorphic to magic square A. Each number in the magic square is mapped to a location in the star. Order-5 is the only size of quadrant magic square that can be transformed to a magic star using all the numbers contained in the square. For that reason, I use the general term 'Iso-like magic stars' to cover all orders.
Isomorphic magic star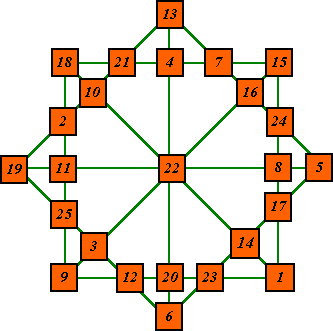		Orders  9, 13, 17, etc magic squares may be used to form this type of star and only if the square is quadrant-magic. Only 25 of the numbers in the magic square can be used, however. Finally, for a given order, only certain magic arrays can be used to form such a star. This order-8 type B star has 12 lines of 5 numbers summing to the magic constant, the same as the order-5 magic square. The outside horizontal and vertical lines (I call these the ‘square’) contain the same numbers in the same order as the outside rows and columns of the magic square. This predetermines two of the numbers, such as the 2 and 21, in each outside diagonal line (I call this the diamond). The corner numbers of the diamond are those that are common to two magic arrays in the quadrant magic square. In this case the 13, 19, 5 and 6 in the plusmagic arrays of square A. This leaves just one number in each side of the diamond to be assigned, and this is the fifth number of the corresponding magic array.

Square B shows the crosmagic arrays. On close examination we see two reasons why an iso-like magic star cannot be formed from this array.

• There are 2 numbers in each array common to the adjacent array instead of 1.
• There are 3 numbers in each diagonal of the array instead of 1.

For any order quadrant magic square the plusmagic array may be used to convert the square to an iso-like magic star.
For orders 8m - 3 the diammagic array may be used but orders 8m+1 fail because of the additional diagonal cells.

All other quadrant magic arrays fail, for every order, due to either or both situations mentioned above.

Please see my Iso-like Magic Stars page for more details and examples of orders 5, 9 and 13 stars.

Order-9 quadrant magic squares

Starting with this order, we identify the patterns by their index numbers.

p1  (plusmagic)	Quadrant magic arrays The same array must appear in all four quadrants of the magic square for it to be called a Quadrant magic square! Quadrant magic squares using this array can form isolike magic stars. However, I have not found such magic squares in order-9.
p2 (sringmagic)	A quadrant magic square with this array cannot be transformed into an isolike magic star because of the 3 cells (instead of 1) that appear on the diagonals. So far, all Quadrant Magic squares found using this array are also lring quadrant magic.
p3  (diammagic)	This array also cannot be used to form an isolike magic star because of the 3 cells (instead of 1) that appear on the diagonals. There are diammagic quadrant magic squares.
p4	This array cannot be used to form an isolike magic star due to both of the reasons explained above. So far, I have found no Quadrant Magic squares using this array. Aale de Winkel found this pattern on Aug. 31, 1999. He also showed mathematically that there can be only 7 totally symmetric patterns for order-9.
p5 (lringmagic)	This array cannot be used to form an isolike magic star because of the 3 cells (instead of 1) that appear on the diagonals. Also, 3 cells instead of 1 appear in the outside rows and columns, and so are common to orthogonally adjacent quadrants.
p6  (crosmagic)	This array  cannot be used to form an isolike magic star because of the 5 cells (instead of 1) that appear on the diagonals. Also, 2 cells instead of 1 appear in the outside rows and columns, and so are common to orthogonally adjacent quadrants. In any case, I have not found such magic squares in order-9.
p7	This array cannot be used to form an isolike magic star because 2 cells instead of 1 appear in the outside rows and columns, and so are common to orthogonally adjacent quadrants. So far, I have found no Quadrant Magic squares using this array.

A pandiagonal sring, lring quadrant magic square

55 25 40 62 23 38 60 21 45 69 3 54 64 7 49 71 5 47 17 32 74 15 30 81 10 34 76 19 43 58 26 41 56 24 39 63 6 48 72 1 52 67 8 50 65 35 77 11 33 75 18 28 79 13 37 61 22 44 59 20 42 57 27 51 66 9 46 70 4 53 68 2 80 14 29 78 12 36 73 16 31

Here the lime green cells are the center of each quadrant and are 1 of the 9 cells in each array. The yellow cells are the lringmagic arrays. I show only 2 of the 4 quadrants for clarity (in the upper left and lower right quadrants). The blue cells are the sringmagic arrays. An order-9 sringmagic square cannot form an isolike magic star because 3 cells instead of 1 are on the main diagonal. An order-9 lringmagic square cannot form an isolike magic star for the same reason given above. Also 3 cells instead of 1 are common with the adjacent quadrant.

All ringmagic quadrant magic squares found to date are both sringmagic and lringmagic (both p2 and p5).

A pandiagonal diammagic quadrant magic square

45 79 71 20 30 46 58 14 6 35 47 57 10 4 41 78 72 25 3 37 76 68 24 36 52 62 11 22 32 51 63 16 8 38 75 64 15 9 43 80 65 21 28 49 59 70 26 29 48 55 13 5 42 81 56 12 1’ 40 77 69 27 34 53 73 67 23 33 54 61 17 2 39 50 60 18 7 44 74 66 19 31

An order-9 diammagic square cannot form an isolike magic star because 3 cells instead of 1 are on the main diagonal. These two types of order-9 quadrant magic squares are the only ones found to date.

Order-9 quadrant magic square questions

There are 7 quadrant magic arrays (totally symmetric patterns) for order-9.
So far only 2 types of quadrant magic squares have been found.

Do sringmagic and lringmagic arrays always appear together?

Do diammagic arrays never appear with sringmagic or lringmagic squares?

Are there NO crosmagic, plusmagic, p4 or p7 order-9 quadrant magic squares?

Are all order-9 quadrant magic squares pandiagonal?

Quadrant Magic Squares Summary

Orders 13 and 17 are on separate pages due to amount of material. See order-13    order-17

My search for quadrant magic squares was performed mostly using Latin prescriptions.
It would be interesting to see results of searches using other methods of magic square generation.
Most of  the quadrant magic squares found (and all orders 9 and 13) are pandiagonal .
Are many regular magic squares quadrant magic?
Are many associated magic squares quadrant magic?
Can there be quadrant magic squares of even order?
    (the quadrants would be n/2 with no central cell in the array.)

All quadrant magic squares found to date  have been a result of searching.
Can an algorithm be developed to generate quadrant magic squares?

Order	Number of magic arrays on these pages	Quadrant magic	Order-13 seems to have the most densely packed quadrant magic squares. Order-13 has a 14-way quadrant magic square. The best I can find for order-17, which should have a great many more combinations, is a 6-way quadrant magic square. So far, all order-13 Quadrant m. s. found are pandiagonal, although regular m. s. have been found for orders 5 and 17.
5	5 but only 2 are unique	2 -way quadrant magic
9	7	2 -way quadrant magic
13	38	14 -way quadrant magic
17	15 ( of a total of 253)	6 -way quadrant magic

Credit

I wish to thank Aale de Winkel for discovering these fascinating magic squares and for all the help he has given me in my attempts to consolidate the features of quadrant magic squares and iso-like magic stars.
As well as suggestions, he provided me lists of his latin prescription squares where he searched for these features, and a program to convert any latin prescription (LP) to an actual magic square.
Please visit his site at http://www.magichypercubes.com/Encyclopedia/index.html then link to quadrantmagic and specialmagic.

Please send me Feedback about my Web site!

Harvey Heinz   harveyheinz@shaw.ca
This page last updated March 11, 2006
Copyright © 1999 by Harvey D. Heinz