 |
 |
 |
 |
 |
 |
Introduction |
A brief introduction to some of the 253 quadrant magic arrays of order-17. |
1-way quadrant magic |
This pandiagonal magic square is p082 (sring quadrant magic). |
2-way quadrant magic |
This pandiagonal square is both p112 and p153 magic. |
3-way quadrant magic |
This pandiagonal square is p209, p213 and p216 magic. |
4-way quadrant magic |
This pandiagonal square is p118, p209, p215 and p241 magic. |
5-way quadrant magic |
This pandiagonal square is p001, p085, p118, p178 and p209 magic. |
6-way quadrant magic |
This pandiagonal square is p070, p153, p172, p178, p215 and p248 magic. |
Regular 1-way quadrant magic |
This regular square is p241 magic but contains at least 1 of each of 15 arrays. |
Regular 3-way quadrant magic |
This regular square is p001 (plus), p082 (sring) and p085 magic. |
Regular 4-way quadrant magic |
This regular square is p153, p172, p178 and p248 magic. |
![]()
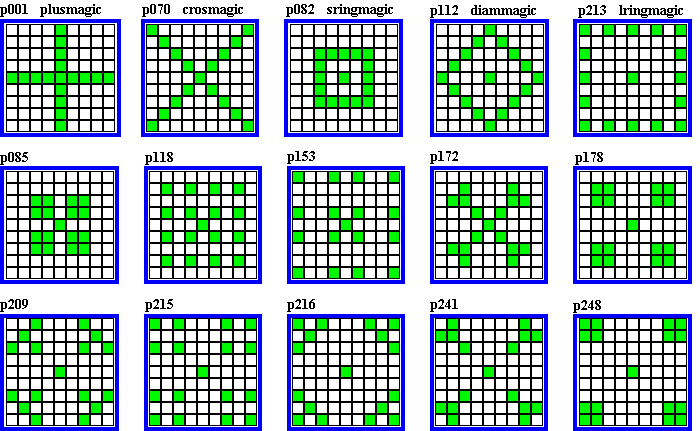
The following 15 patterns are a sample from the set of 253 quadrant magic arrays of order-17.
This is the highest of 10 types of magic arrays as determined by degree of
symmetry, and is the only type used to form quadrant magic squares..
For order-17, the quadrants are 9 x 9 cells. The magic array has 16 cell plus the
quadrant's center cell, that together must sum to the magic constant.
Remember, to be quadrant magic, a magic square must have 4 identical
arrays in the 4 quadrants.
The plusmagic (p001) quadrant magic square is the only type that can transform into an
order-17 iso-like magic star.
Quadrant magic squares and arrays were investigated jointly by Aale de
Winkel and myself during the period of May to September, 1999.
Please visit his site at
http://www.magichypercubes.com/Encyclopedia/index.html.
(Use your 'Back' button to return to this page.)
 Examples:
Examples:| The sets of 4 identical arrays that occupy the 4 quadrants of the example quadrant magic squares | ||||||||||||||||||
| Type | LP (Latin Prescription) | p 001 |
p 070 |
p 082 |
p 085 |
p 112 |
p 118 |
p 153 |
p 172 |
p 178 |
p 209 |
p 213 |
p 215 |
p 216 |
p 241 |
p 248 |
# of arrays | |
| Sqr. | Quad | |||||||||||||||||
| Pan | (2,3,0)(2,11,0) | . | . | @ | . | . | . | . | . | . | . | . | . | . | . | . | 11 | 7 |
| Pan | (1,8,0)(2,1,0) | . | . | . | . | @ |
. | @ |
. | . | . | . | . | . | . | . | 8 | 5 |
| Pan | (1,10,0)(12,15,0) | . | . | . | . | . | . | . | . | . | @ | @ | . | @ |
. | . | 14 | 8 |
| Pan | (7,11,0)(11,7,0) | . | . | . | . | . | @ | . | . | . | @ |
. | @ |
. | @ |
. | 12 | 10 |
| Pan | (5,14,0)(14,5,0) | @ |
.. | . | @ |
. | @ | . | . | @ | X | . | . | . | . | . | 13 | 9 |
| Pan | (10,12,0)(12,10,0) | . | @ |
. | . | . | . | X | @ | @ | . | . | X |
. | . | @ |
15 | 15 |
| . | . | . | . | . | ||||||||||||||
| Reg | (7,11,0)(8,8,0) | . | . | . | . | . | . | . | . | . | . | . | . | . | @ |
. | 15 | 15 |
| Reg | (8,8,0)(14,1,0) | @ |
. | @ | @ | . | . | . | . | . | . | . | . | . | . | . | 14 | 10 |
| Reg | (8,8,0)(12,10,0) | . | . | . | . | . | . | @ | @ | @ | . | . | . | . | . | @ |
12 | 8 |
| ..@ | = this array shown in diagram | ..X | = this array is present in all quadrants but not shown in diagram |
The last two columns show the total number of magic arrays that are present at least once in the square, and the number in the most populated quadrant.
![]()

This square is P082 (sring) quadrant magic but contains 11different quadrant magic arrays, 7 in the upper right quadrant.
This and the following quadrant magic squares show the center cell of each quadrant green. This cell is common to all the magic arrays in that quadrant of the square. It is LP (2, 3, 0)(2, 11, 0).
![]()

This square is P112 (diam) and p153 quadrant magic. It contains 8
different quadrant magic arrays, 5 in the upper left quadrant.This one is LP (1, 8, 0)(2,
1, 0).

![]()

This square is p209, p213 and, p216 quadrant magic. It contains 14 different quadrant magic arrays, 8 in the upper right quadrant. It is LP (1, 10, 0)(12, 15, 0). Here blue indicates p209, yellow p213 (lring) and violet p216.
Showing multiple magic arrays in the same diagram can be confusing when the arrays
share cells in the common row or common column. I will use green to indicate all cells
that are common to 2 adjacent arrays (as well as the central cell of each quadrant).
Keep in mind, however, that each array actually appears in all 4 quadrants of the magic
square.
![]()

This square is p118, p209, p215 and, p241 quadrant magic. It contains 12 different quadrant magic arrays, 10 in the upper right quadrant. This is LP (7 ,11, 0)(11, 7, 0). P118 is blue, p209 is yellow, p215 is violet and p241 is red..

This square is p001 (plus), p085, p118, p178 and p209 quadrant magic. It contains 12
different quadrant magic arrays, 10 in the upper left quadrant.
P001 (plus) is blue, p085 is yellow, p118 is violet and p178 is red. Not shown is p209.

This square is p070, p153, p172, p178, p215 and, p248 quadrant magic. It contains all
15 different quadrant magic arrays and all 15 in the upper left quadrant. This is LP (10,
12, 0)(12, 10, 0).
P070 (cros) is blue, p172 is yellow, p178 is violet and p248 is red. Not shown is p153 and
p215.
A reminder; this study involves a search for only 15 of the 253 quadrant magic arrays
of order-17.
Each quadrant magic square shown on this page actually contains many more of the 253
order-17 quadrant magic arrays.

This square has only the p241 quadrant magic array in all 4 quadrants.
However, it contains at least 1 copy of all 15 different quadrant magic arrays, and all 15
appear in the upper left quadrant. It is LP (7, 11, 0)(8, 8, 0)
It, and the following 2 examples are regular (not pandiagonal magic
squares,
![]()

This square is a regular p001, p 082 and p085 quadrant magic square. It contains 14
different quadrant magic arrays with 10 in the upper right quadrant. It is LP (8, 8,
0)(14, 1, 0).
Blue is p001 (plus), yellow is p082 (sring), violet is p085, green is quadrant centers and
cells common to 2 adjacent arrays.
Notice that all regular (not pandiagonal) quadrant magic squares shown here have 1 of the 2 LP vectors as (8, 8, 0).
Some reminders:
All magic arrays shown appear in all 4 quadrants of the magic square.
Some patterns appear to be smaller then others, but all are considered to occupy the
entire quadrant of the magic square.
The central row and central column of the magic square is common to the 2 adjacent
quadrants.
![]()

This square is a regular p153, p172, p178 and p248 quadrant magic square. It contains
12 different quadrant magic arrays with 8 in the upper left and upper right quadrants.
This is LP (8, 8, 0)(12, 10, 0).
Blue is p153, yellow is p172, violet is p178 and red is p248.
![]()
Quadrant magic arrays are the most symmetrical of 10 classes of magic arrays. It is the only type of magic array considered on these pages, and the only type (by definition) that can form quadrant magic squares.
The magic squares shown on this page were found by searching for only 15 of the
253 order-17 quadrant magic arrays. If a search is conducted for all 253 quadrant magic
arrays:
What is the largest possible number of 4 identical
arrays to appear in the same magic square?
What is the largest number that appears at least once in the same magic
square?
What is the largest number that appears in the same quadrant of the same
magic square?
I have shown at least 1 example of a quadrant magic square formed from
each of the 15 arrays searched for.
Can magic squares be formed using each of the 253
quadrant magic arrays?
![]()
Please send me Feedback about my Web site!
Harvey Heinz harveyheinz@shaw.ca
This page last updated
March 11, 2006
Copyright © 1999 by Harvey D. Heinz