Material from REC

Recreational & Educational Computing is a 14 to 18 page newsletter published 6 times a year by Dr. Michael Ecker.

REC Focus: Stimulating mathematics, recreation, education, programming, graphics, and other computer activity.

Dr. Ecker has several subsidiary programs to compliment REC, such as:
REC-on-Disk which includes the paper version plus all programs plus additional material
Mathematical Farragoes each of which are multiple disk collections of contributed programs.

More information at:
Visit REC's web site at http://members.aol.com/DrMWEcker/REC.html
Or contact Dr. M. W. Ecker via e-mail at MWE1@PSU.edu or DrMWEcker@AOL.com

I thank Dr. Ecker for permission to show here several magic squares previously published in REC.
And , of course, I thank the authors for their ingenuity and hard work.

Order-5 Palindrome Magic square	Order-4 and order-5 magic squares consisting only of palindromes.
Consecutive Prime Numbers Order-9	An order-9 magic square consisting of 81 consecutive primes.
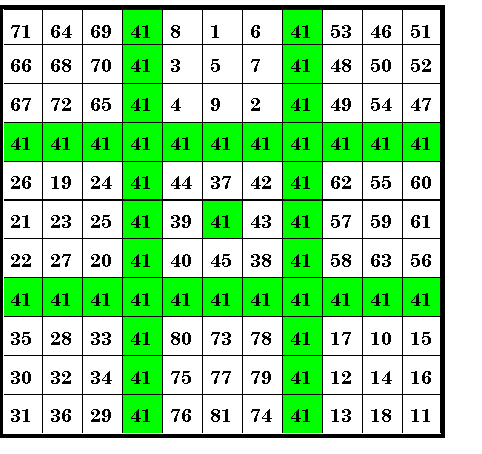
Forty-one	This order-11 magic square includes 41 fortyones.
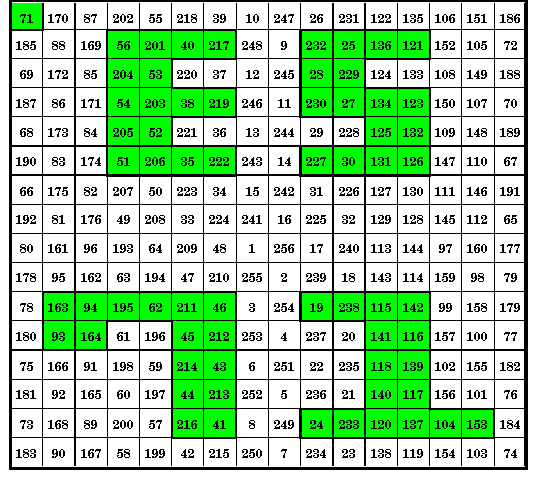
E.S.-71	This order-16 magic square includes the authors initials and year of construction.
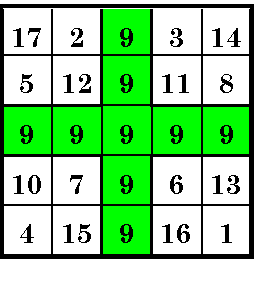
Number-Nine Magic Square	An order-4 magic square changed into an order-5 by adding 8 additionaal nines.
Order-16 Prime Number Magic Square	With inlaid orders 4, 6, 8, 10, 12, 14 magic squares of primes.
Order-6 Prime Magic Star	This star uses 19 consecutive prime numbers in 9 lines of 5.

Order-5 Palindrome Magic square

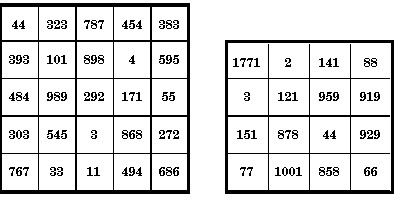
REC_pali.gif (5024 bytes) Alan W. Johnson, Jr., REC vol.5, No. 8. December 1990,Page 4

Written to celebrate the palindromic year 1991., the 25 palindromes of this order-5 square have the magic sum 1991.

Adding 11 (another palindrome) to 1991 gives the next palindrome year 2002, the sum of this order-4 magic square. It consists of 16 different palindromes

Consecutive Prime Numbers Order-9

REC_pri9.gif (9976 bytes)

Alan W. Johnson, Jr., REC vol. 7 No. 7. February1993,Page 10

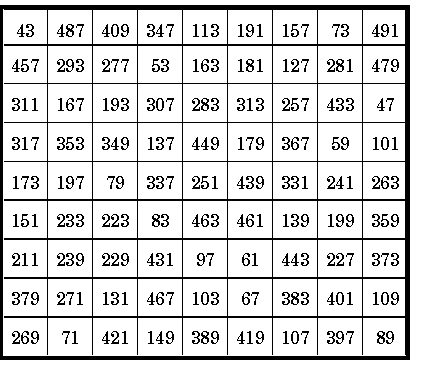
This order-9 magic square is composed of the 81 consecutive prime numbers 43 to 491. The magic sum is the prime number 2311.

Forty-one

REC_41.gif (13874 bytes)

E. W. Shineman, Jr., REC vol.8 No. 1 & 2. July 1993,Page 5

This order-11 magic square consists of a normal order-9 composite magic square divided into it's nine order-3 magic squares with 40 additional forty-ones. The magic constant is 11 x 41. Mr. Shineman constructed this square to celibrate the year 1941!

The magic constant of each of the nine order-3 magic squares themselves form an order-3 magic square, a feature of all composite magic squares.
The principal holds for any number substituted for 41, as long as the starting number is such that the middle number of the series is the number you wish to substitute for 41.

E.S.-71

REC_71.gif (19836 bytes) E. W. Shineman, Jr., REC vol.8 No. 3 & 4. July/August/September 1993,Page 17

This order-16 magic square is pandiagonal so broken diagonals also sum to the constant 2056, as well as each of the authors initials and the two figures of the year of creation (1971).

It may also be considered an ornate magic square because of the inlaid figures (E, S, 7 and 1). Of course, if you make use of the pandiagonal feature to tranform it to a different magic square by moving columns or rows from one side to the other , this ornate feature would disappear.

Number-Nine Magic Square

REC_9.gif (4728 bytes) E. W. Shineman, Jr., REC vol.10 No. 3 & 4. December 1995-January 1996,Page 1

An order-5 magic square constructed from the series of numbers from 1 to 17, but with 8 additional (total of 9) nines .

The magic sum = 45. Note that 9 = 4 + 5 which is also the two orders involved. Also, the outer four order-2 squares are not magic but the four cells of each sum to 36 and 3 + 6 = 9.

This is classified as an ornate magic square. It is not a pure or normal one because it doesn't consist of a series of numbers from 1 to n².

Order-16 Prime Number Magic Square

Alan W. Johnson, Jr., REC vol.6, No. 1 & 2. March 1991,Page 13

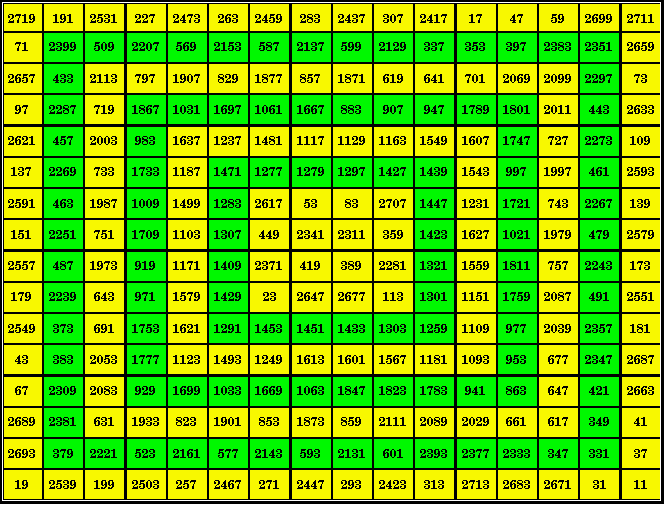
REC_Pr16.gif (25570 bytes)

This magic square contains inlays of each even order magic square from 4 to 14. It looks like a concentric or bordered magic square, but this square has the low and high numbers scattered throughout the square. With a true bordered magic square, one half the numbers in the border consists of the low numbers in the series, the other half are the high numbers.

Here each square has all rows, columns and main diagonals equal to the magic constant for that square, as follows:
Order-4         5460                                        Order-10        13650                                      Order-14         19110
Order-6         8190                                        Order-12        16380                                      Order-16         21840
Order-8       10920
The magic sums differ by a constant 2730.

Prime Number Star

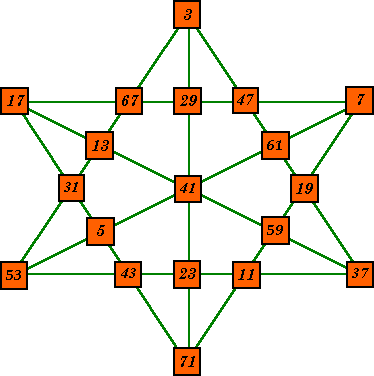This magic star uses the prime numbers from 3 to 71. Each of the 9 lines of 5 numbers sums to the prime number 167.

It was designed by Allan Wm. Johnson, Jr. of Washington, DC and was published in Recreational & Educational Computing, Vol. 15, Nos. 2 & 3, page 21.

Used by permission.

Please send me Feedback about my Web site!