 |
 |
|
 |
 |
 |
This page is one of 4 on this subject
Please enjoy them all! |
Swap columns only |
Examples by swapping columns 1 & 2 and columns 3 & 4. |
Swap rows only |
Examples by swapping rows 1 & 2 and rows 3 & 4. |
Diagonals to rows |
Works on any order-4 pandiagonal or semi-pandiagonal magic square. |
A double magic square loop |
Sets of four order-4 magic squares where each number differs by 4 (modulo 16). |
...Quadruplets |
A pair of magic squares related by +8. Their complements are another loop. |
...Triplets |
A loop of three magic squares using +4 and +8 with +12 returning to the original. |
...Pairs |
Two different loops of two magic squares using CPI and +8. |
Congruent modulo 8 |
If # < 9 new number = # + 8, if # > 8 then new # = # - 8. |
Intro to Order-4 Transforms. |
Back to the introduction page to this subject. (Also up arrow above and at end). |
Summary |
More transformations and a Table of over 45 order-4 transformations. |
![]()
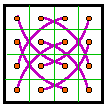
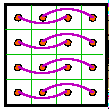
The second magic square of each pair is a result of swapping columns 1 and two and
columns 3 and 4. In many cases this magic square is either rotated or reflected from the
normalized position.
Notice that the complementary pair diagrams are a great help in visualizing row and column
interchanges.
 |
#102 I #785 I 1 8 10 15 8 1 15 10 12 13 3 6 13 12 6 3 7 2 16 9 2 7 9 16 14 11 5 4 11 14 4 5 |
 |
#22 II #592 II 1 4 14 15 4 1 15 14 13 16 2 3 16 13 3 2 12 9 7 6 9 12 6 7 8 5 11 10 5 8 10 11 |
 |
#120 III #487 III 1 8 14 11 8 1 11 14 12 13 7 2 13 12 2 7 15 10 4 5 10 15 5 4 6 3 9 16 3 6 16 9 |
 |
#93 IV #664 IV 1 7 14 12 7 1 12 14 16 10 3 5 10 16 5 3 11 13 8 2 13 11 2 8 6 4 9 15 4 6 15 9 |
 |
#33 V #578 V 1 4 16 13 4 1 13 16 14 15 3 2 15 14 2 3 11 10 6 7 10 11 7 6 8 5 9 12 5 8 12 9 |
 |
#48 VI-P #824 VI-P 1 6 11 16 6 1 16 11 12 15 2 5 15 12 5 2 8 3 14 9 3 8 9 14 13 10 7 4 10 13 4 7 |
| 96 of the group VI magic squares are semi-pandiagonal. These
96 squares are linked in pairs by the above column interchange (and also by the row
interchange shown below). However, there are another 208 magic squares of order-4 group
VI that are only simple magic squares. The reason they are group VI is because they have
the same complementary pair pattern as the 96 semi-pandiagonal group VI. |
 |
#144 VI-S not magic 1 10 15 8 10 1 8 15 14 11 4 5 11 14 5 4 3 6 13 12 6 3 12 13 16 7 2 9 7 16 9 2 #144 is one of the 208 group VI that is not semi-pandiagonal. |
|
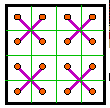
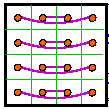
The second magic square of each pair below is a result of swapping rows 1 and two and
rows 3 and 4. In many cases this magic square is either rotated or reflected from the
normalized position.
This is a companion transformation to the one presented above and has the same conditions.
However, the partner magic square in each case is different. To illustrate, I will use the
same origin square for each group.
 |
#102 I #828 I 1 8 10 15 12 13 3 6 12 13 3 6 1 8 10 15 7 2 16 9 14 11 5 4 14 11 5 4 7 2 16 9 |
 |
#22 II #446 II 1 4 14 15 13 16 2 3 13 16 2 3 1 4 14 15 12 9 7 6 8 5 11 10 8 5 11 10 12 9 7 6 |
 |
#120 III #297 III 1 8 14 11 12 13 7 2 12 13 7 2 1 8 14 11 15 10 4 5 6 3 9 16 6 3 9 16 15 10 4 5 |
 |
#93 IV #326 IV 1 7 14 12 16 10 3 5 16 10 3 5 1 7 14 12 11 13 8 2 6 4 9 15 6 4 9 15 11 13 8 2 |
 |
#33 V #229 V 1 4 16 13 14 15 3 2 14 15 3 2 1 4 16 13 11 10 6 7 8 5 9 12 8 5 9 12 11 10 6 7 |
 |
#48 VI-P #763 VI-P 1 6 11 16 12 15 2 5 12 15 2 5 1 6 11 16 8 3 14 9 13 10 7 4 13 10 7 4 8 3 14 9 |
Summery
These two transformations work for all 288 magic squares of groups I to V.
They also work for the 96 semi-pandiagonal magic squares of group VI.
In each case they produce a partner magic square of the same group.
They do not work for the 208 simple magic squares of group VI.
They also do not work for any of the 240 magic squares of groups VII to XII.
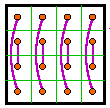
A third related transformation in which both the rows and columns are exchanged will
produce a magic square in the same group, for all 12 groups.
There are a number of other row and/or column interchanges that also transform one magic
square into another one. They are summarized in the table at the bottom of this page.
![]()
 |
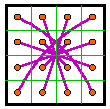
This transformation works for all of group I to Group VI-P (the semi-pandiagonal) magic squares. It also works for 48 of the 208 group VI-S simple magic squares. If the diagonals are converted to columns instead of rows, the same magic squares are produced but rotated. |
|
 |
102 I 173 V 1 8 10 15 1 13 16 4 12 13 3 6 12 8 5 9 7 2 16 9 7 11 10 6 14 11 5 4 14 2 3 15 |
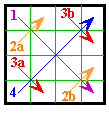
By converting diagonals to rows as per the above diagram, the 48 group I
are transformed to 48 group V. Note that #173 shown here is not normalized. |
 |
32 V 201 I 1 4 16 13 1 15 10 8 14 15 3 2 14 4 5 11 7 6 10 1 7 9 16 2 12 9 5 8 12 6 3 13 |
Whether the transformation is to a group I or a group V is determined by the orientation of the complement pairs of the originating magic square. |
 |
173 V 103 V 1 12 7 14 1 8 10 15 13 8 11 2 13 12 6 3 16 5 10 3 16 9 7 2 4 9 6 15 4 5 11 14 |
When converting Group V magic squares by diagonals to rows, 48 transform to the 48 group I, the other 48 transform to another group V magic square of the same orientation. |
This transformation is not universal. It works only on some order-4 magic squares.
The top row of magic squares is a loop obtained by adding 4 to each number of the
preceding square. Adding 4 to each number of the last square gets you back to the first
magic square, making a loop of four magic squares.
The second row of magic squares are, in each case, the complement of the square above.
They form another loop of four magic squares, this time by subtracting four from each
number.
As mentioned in the previous section, the complement belongs to the same group as the
original magic square. Also, as mentioned in the previous section, the complement is a
disguised version of the fundamental magic square for the index number shown. (In the
first loop, all but the first magic square (the original) are disguised versions of the
index # shown.)
#109
I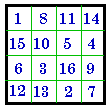 |
+ 4 = | #326
IV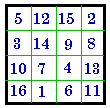 |
+ 4 = | #621
I |
+ 4 = | #467
IV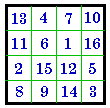 |
#469
I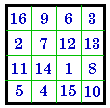 |
- 4 = | #93
IV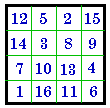 |
- 4 = | #294
I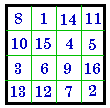 |
- 4 = | #664
IV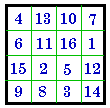 |
In a paper called Magic Squares of Order-4 and their Magic Square Loops1, Robert
S. Sery investigates all 880 order-4 for such loops. He found:
Octuplets …...... 6 pairs of loops of 4 magic squares each .........6 x 8 =
48
Quadruplets .. ..64 pairs of loops of 2 magic squares each .......64 x 4 = 256
Triplets ……... 16 loops of 3, no CPI involved .......................16 x 3 =
48
Pairs ………. 232 loops of twins by CPI or by adding 8 .......232 x 2 =
464
Singles …….... 64 with no connections to others, all type VI .. 64 x 1 =
64
Total
...................................................................................................
880
The singles are all self-similar magic squares because the complement of each is a
reflected copy of itself.
Examples of the quadruplets, triplets and pairs follow.
1. Robert S. Sery, Magic squares of order-4 and their Magic Square Loops, Journal of Recreational Mathematics, vol. 29(4) 274-281, 1998 (Dated 1998 but only released in May, 2000)
![]()
8 VIII 1 3 16 14 8 15 2 9 13 6 11 4 12 10 5 7 |
+ 8 = | 605 VIII 9 11 8 6 16 7 10 1 5 14 3 12 4 2 13 15 |
Adding 8 (modulo 16) to each cell of index #8 magic square
produces a disguised version of index # 605 and, of course adding 8 to each cell of this
version of #605 reproduces #8. The complements of these two magic squares produce #409 and # 242 which together form a
similar loop. |
409 VIII 16 14 1 3 9 2 15 8 4 1 6 13 5 7 12 10 |
+ 8 = | 242 VIII 8 6 9 11 1 10 7 16 12 3 14 5 13 15 4 2 |
This loop consists of 3 magic squares before looping back to the starting square. It
uses three different addition constants (modulo 16 of course). This is one of 16 such sets
of three.
Note that the paired loop consists of the same 3 magic squares but in a different
orientation.
Also, in the second loop, the positions of squares 655 and 652 are reversed.
#38 VI 1 5 12 16 15 11 6 2 10 4 13 7 8 14 3 9 |
+ 4 = | 655 X 5 9 16 4 3 15 10 6 14 8 1 11 12 2 7 13 |
+ 8 = | 652 X 13 1 8 12 11 7 2 14 6 16 9 3 4 10 15 5 |
+ 12 = | #38 VI 1 5 12 16 15 11 6 2 10 4 13 7 8 14 3 9 |
#38 VI 16 12 5 1 2 6 11 15 7 13 4 10 9 3 14 8 complement of 38 (above) |
+ 4 = | 655 X 4 16 9 5 6 10 15 3 11 1 8 14 13 7 2 12 complement of 652 (above) |
+ 8 = | 652 X 12 8 1 13 14 2 7 11 3 9 16 6 5 15 10 4 complement of 655 (above) |
+ 12 = | #38 VI 16 12 5 1 2 6 11 15 7 13 4 10 9 3 14 8 complement of 38 (above) |
Because the complement of # 38 is a reflected version of itself, #38 is a self-similar magic square (Suzuki).
![]()
#3 XII 1 2 16 15 13 14 4 3 12 7 10 5 8 11 6 9 |
CPI = | 209 XII 16 15 1 2 4 3 13 14 5 10 7 12 9 6 11 8 |
Unlike the other loop examples presented, this is not a pair of loops but
individual loops of two magic squares. This top loop is accomplished by complementing
the #3 magic square to obtain the #209 square. |
12 VI 1 4 13 16 8 14 3 9 15 5 12 2 10 11 6 7 |
+ 8 = | 218 XII 9 12 5 8 16 6 11 1 7 13 4 10 2 3 14 15 |
Here the constant 8 has been added to each number in magic square # 12 to
obtain the #218 square. In each case the same operation loops back to the original magic square. There are 232 pairs of magic squares that make such loops. |
![]()
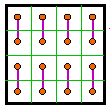
If you replace each number in the order-4 magic square with its congruent mod (8) number, a new magic square of the same group is obtained. In effect, if the number in the original magic square is less then 9, the new number is the number plus 8. If the number in the original magic square is greater then 8, the new number is the number minus 8.
This works for all magic squares belong to Groups I, II, III, IV, V, VI-P, VII and
VIII.
For Groups VI-S, IX, X, XI and XII, the rows and columns sum correctly, but the diagonals
are incorrect.
Short-cut number swap
| Original decimal number | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| After congruent mod (8) swap | 9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Three examples
Original Transform Original Transform Original Transform 104 I 623 I 478 III 632 III 148 V 720 V 01 08 10 15 09 16 02 07 03 06 13 12 11 14 05 04 01 10 16 07 09 02 08 15 14 11 05 04 06 03 13 12 16 09 02 07 08 01 10 15 15 08 02 09 07 16 10 01 07 02 16 09 15 10 08 01 10 15 08 01 02 07 16 09 04 11 13 06 12 03 05 14 12 13 03 06 04 05 11 14 05 04 11 14 13 12 03 06 14 05 03 12 06 13 11 04
This method was suggested by Yvan Saint-Pierre in an e-mail dated Sept. 8, 2000.
Please send me Feedback about my Web
site!
![]()
![]()
![]()

Last updated
September 01, 2009
Harvey Heinz harveyheinz@shaw.ca
Copyright © 2000 by Harvey D. Heinz