Order-4, Transformations & Patterns

Introduction

On this page I will discuss ways of transforming one magic square into another one. Also I will discuss various patterns and the use of patterns for classification.

The magic squares discussed will all be order-4 because;

1. The only order for which all magic squares are known (except for the one order-3).
2. There are a suitably large number of magic squares to work with.
3. The small size makes it quicker to form the magic squares and easier to see the patterns.

Methods described here may be extended to work with higher orders.

The transformations discussed will be from pure magic squares (those using numbers from 1 to 16) to pure magic squares.
However, it is worth mentioning here that any magic square may be converted to another magic square (not pure) simply by applying any constant to each number in the square using any arithmetic operator. In many cases, if a constant is applied to the units digit of each number, and a different constant applied to the ten's digit of each number, the result will also be a magic square.

The transformation principles may be extended also to work with higher dimensions (cubes, tesseracts, etc).

Two sources for the complete set of order-4 magic squares are:
W. H. Benson & O. Jacoby, New Recreations With Magic Squares, Dover Publications, Inc, 1976, 0-486-23236-0
Matsumi Suzuki's Magic Squares web page are now found in the MathForuml
(Note however that Suzuki's list is not normalized or in index order.)
Since this page was originally written, I have written and ran a program to find all order-4 magic squares.
The various lists may be found from my Order-4 Lists page.

Order-4 groups

There are 880 basic magic squares of order-4. The complete set was published in 1693. (Frénicle de Bessey, Des Quarrez Magiques. Acad. R. des Sciences).
They were classified into 12 groups by H. E. Dudeney and first published as such in The Queen, Jan. 15, 1910. It (the classes) appeared later in Amusements in Mathematics, 1917 published by Thomas Nelson & Sons, Ltd.

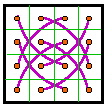Group I	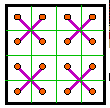Group II	Group III	Group IV	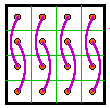Group V	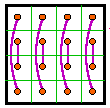Group VI
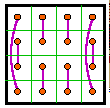Group VII	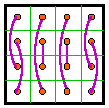Group VIII	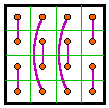Group IX	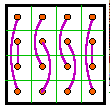Group X	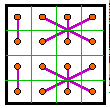Group XI	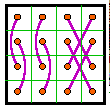Group XII

The 12 groups
The 12 groups are classified by the patterns formed by the 8 complement pairs.
A complement pair is two numbers that together sum to n² + 1. For order-4 that number is 17.

Normalized position & Magic Lines

Any magic square can appear in 8 different aspects due to rotations and reflections. For enumeration purposes, one of these 8 squares must be designated as the fundamental or basic one. The other 7 are often referred to as disguised versions of this one.

Frénicle # 175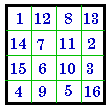 A.	Rotated 90°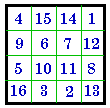 B.	Rotated 180°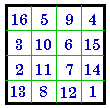 C.	Rotated 270°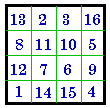 D.	Dudeney group III E.
Horizontal Reflection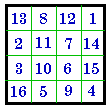 F.	Vertical Reflection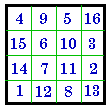 G.	Vertical then 90°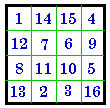 H.	Horizontal then 90°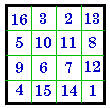 I. Dürer  square	Magic line pattern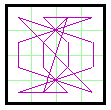 J. for square A.

Here we use Frénicle's # 175 as an example to illustrate how one fundamental magic square can also appear in 7 disguised versions. All 8 aspects are Dudeney group III so are associated magic squares.
Note that whether the magic square is rotated right or left is arbitrary. Here I use right (clockwise) rotation.
H. may also be considered as reflected around the leading diagonal and I. as being reflected around the right diagonal .
I. is the magic square from Albrecht Dürer’s engraving, Melancholia, 1514.

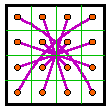
The magic line pattern  at J. is constructed by following the magic square numbers of A.  in sequence. To the left is the same diagram with some of the areas filled in. This may be done in various ways to produce artistic designs. As well as making pretty patterns, these are sometimes used for classification purposes. Jim Moran has a lot of material on these in The Wonders of Magic Squares, Random House, 1982, 0-394-74798-4. He refers to these as sequence designs.

Normalized position

For enumerating and listing the magic squares of a given order, one of the eight above positions must be designated the normal position. This standard prevents confusion and permits easy comparison. Frénicle established two simple rules to determine the standard position for order-4. These same rules may be used for all other orders as well.

1. The smallest number in any corner of the magic square must be in the top left corner. If it is not, rotate the square until it is.
2. The second number in the top row must be of lower then the first number in the second row. These are the two numbers adjacent to the one in the top left corner.

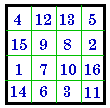
Notice that magic square A. (# 175 above) and  # 727 (below) satisfy these two conditions.

More on Magic Lines

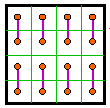
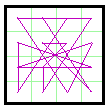
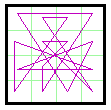
Normally magic lines are drawn between the centers of the cells. However, this sometimes results in a longer line hiding a shorter one.
Shown here are two versions of magic line diagrams for magic square #727 (Group VIII).
For interest, each is also shown with some areas filled in, forming a type of abstract art.

In the first line diagram, notice that the top line from 12 to 13 is covered up by the line from 4 to 5. In fact, it looks like the line goes from 4 to 12 to 13 to 5.
Likewise the left line looks like it is going from 14 to 1 to 15.
These concerns are resolved by offsetting the necessary lines as I did with the second diagram.
Which  method is actually used is a matter of personal preference. The first method looks tidier because all points appear as on a regular grid pattern. The second method gives a truer picture.

Complementing

Any order of magic square may be transformed to another magic square simply by subtracting each number in turn from
n² + 1.
The resulting magic square is a disguised version of another magic square belonging to the same group.

A.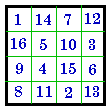 #202            XI

B.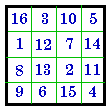 Complement of A.

C.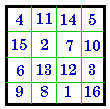 B. Normalized = #724

D. Group XI

E. Line pat. for A. & B.

The resulting magic line diagram will be exactly the same for the original and the complement magic squares. You simply move around it in the opposite direction. However, it requires rotation for the normalized version of the complement.
This may be considered complementing the magic square. Robert Sery refers to the process as complementary pair interchange (CPI).

When complementing some magic squares you end up with the original square except that it is rotated or reflected. Any order of associated (group III) magic square is of this type and the complement will be rotated 180 degrees. Any magic square with a complementary pair pattern like that of group VI also has this self-similar pattern with the complementary reflected either vertically or horizontally, depending on the orientation of the pattern. See my Self-similar page for more information on this type of magic square.

Swapping rows and columns

Complementing each number in a magic square will ALWAYS produce a magic square in the same group.
The following row and column swaps will also always produce an order-4 magic square.
Swap rows and columns 1 and 4
Swap rows and columns 2 and 3.
Change row and column orders to 2, 1, 4, 3.
Change row and column orders to 3, 1, 4, 2.
However, the resulting magic square is likely to belong to a different group. See the bold lines in the Summary table.

Transformations from a pandiagonal magic square

A. # 204 is the pandiagonal magic square example used in this section.
B. is it's complement, # 744 (disguised). All pandiagonal magic squares create new pandiagonals when complemented.
C. is the magic square obtained by adding 8 mod(16) to each number. It also is a disguised # 744. However, complementing   and adding 8 mod(16) to each number sometimes give different magic squares. See. # 117 whose complement is # 483 and  +8 is # 646.
D. is obtained by exchanging the two outside columns and also the two outside rows. However, it is no longer pandiagonal but a group II, (# 63 disguised). Any magic squares can be transposed to another with this method.
E. is the Dudeney pattern for all pandiagonal (group I) magic squares.
F. is the magic line pattern for the example, # 204. Other pandiagonal magic squares will have other patterns.

A. #204        I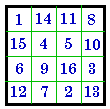

B. #744        I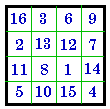

C. #744        I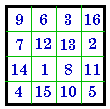

D. #63           II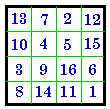

E. Type I

F. for # 204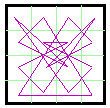

Following is a set of 15 transformations that work only with pandiagonal magic squares and result in other pandiagonal magic squares.
Here we move a row from the top to the bottom of the magic square, a column from the left to the right, or both a row and a column.
All of these magic squares are disguised except # 469, and of course, the original, # 204.
I have used leading zeros simply to allow simpler formatting.

Rows/columns             No
                          column change            1 col.                     2 col.                    3 col.

no row change   Original # 204       # 109                     #396                      #294
                           01  14  11  08       14  11   08  01       11  08  01  14        08  01  14  11
                           15  04  05  10       04   05  10  15       05  10  15   04       10  15  04  05
                           06  09  16  03       09  16   03  06       16  03  06  09        03  06  09  16
                           12  07  02  13       07   02  13  12       02  13  12   07       13  12  07  02

1 row                   # 171                    #107                      #691                      #788
                           15   04  05  10       04  05   10  15       05  10  15  04        10  15  04  05
                           06   09  16  03       09  16  03   06       16  03  06  09        03  06  09  16
                           12   07  02  13       07  02  13   12       02  13  12  07        13  12  07  02
                           01   14  11  08       14  11  08   01       11  08  01  14        08  01  14  11

2 rows                 # 560                     #621                      #744                      #469
                           06   09  16  03       09  16  03   06       16  03  06  09        03  06  09  16
                           12   07  02  13       07  02  13   12       02  13  12  07        13  12  07  02
                           01   14  11  08       14  11  08   01       11  08  01  14        08  01  14  11
                           15   04  05  10       04  05  10   15       05  10  15  04        10  15  04  05

3 rows                 # 532                     #839                      #355                      #292
                           12   07  02  13       07  02  13   12       02  13   12  07       13  12  07  02
                           01   14  11  08       14  11  08   01       11  08  01  14        08  01  14  11
                           15   04  05  10       04  05  10   15       05  10  15  04        10  15  04  05
                           06   09  16  03       09  16  03   06       16  03  06  09        03  06  09  16
This set contains 16 magic squares out of the 48 pandiagonal magic squares of order-4. Thus all 48 pandiagonal magic squares can be derived from 3 essentially different magic squares.
Any one of these 16 magic squares could be considered to be the origin of the set of 16. If the lowest index number is taken as the starting square, then the other two sets of 16 would start with #104 and # 116.

Transformations between associated magic squares

Here are 15 ways to transform an associated magic square to another associated magic square (there are many more).
The result is 10 different group III magic squares with 5 of these appearing twice.
Complementing is not included here because, as mentioned previously, you obtain only a disguised version of the original.
The original is normalized as are 2 of the resulting magic squares. The other 13 are all disguised versions of their index number.

#126     III            #124 Exchange           #206 Exchange           #183 Exchange rows

Original                rows  1 and 4          columns 1 and 4          and columns 1 and 4

 1  8 15 10               7  2  9 16              10  8 15  1              16  2  9  7

14 11  4  5              14 11  4  5               5 11  4 14               5 11  4 14

12 13  6  3              12 13  6  3               3 13  6 12               3 13  6 12

 7  2  9 16               1  8 15 10              16  2  9  7              10  8 15  1



#206 Exchange        #478 Exchange rows      #308 Swap col. 1 and 2     #632 Swap rows and

columns 2 and 3     1 and 2 with 3 and 4       with col. 3 and 4       col. 1 and 2, 3 and 4

 1 15  8 10              12 13  6  3              15 10  1  8               6  3 12 13

14  4 11  5               7  2  9 16               4  5 14 11               9 16  7  2

12  6 13  3               1  8 15 10               6  3 12 13              15 10  1  8

 7  9  2 16              14 11  4  5               9 16  7  2               4  5 14 11



#124  Exchange       #789 Move quadrants      #289 Move quadrants         #632 Swap kitty-

rows 2 and 3              clockwise            counter-clockwise          corner  quadrants

 1  8 15 10              12 13  1  8              15 10  6  3                6  3 12 13

12 13  6  3               7  2 14 11               4  5  9 16                9 16  7  2

14 11  4  5               6  3 15 10               1  8 12 13               15 10  1  8

 7  2  9 16               9 16  4  5              14 11  7  2                4  5 14 11



#183 Swap columns       #478 swap rows          #395 swap columns        #741 Swap columns and

and rows 2 and 3       1 and 2, 3 and 4         1 and 2, 3 and 4        rows 1 and 2, 3 and 4

 1 15  8 10              14 11  4  5              15  1 10  8                4 14  5 11

12  6 13  3               1  8 15 10               4 14  5 11               15  1 10  8

14  4 11  5               7  2  9 16               6 12  3 13                9  7 16  2

 7  9  2 16              12 13  6  3               9  7 16  2                6 12  3 13

Transformation between groups

In almost all cases, the resulting magic square will be a disguised version of the index number shown.

Between Group I and II by exchanging rows 2 and 3 and columns 2 and 3.
Each of the 48 group I magic squares transforms to one of the 48 group II.
In this and all following cases the transformation works in reverse, so in this case, group II can also be transformed to group I

#171        I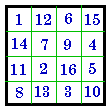

Group I

Exchange rows 2 & 3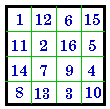

and col. 2 & 3 = #57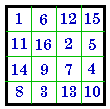

Group II

The same result is obtained by swapping rows and columns 1 and 4 instead of 2 and 3. The same index number magic square is obtained but it is a reflected version.

Between Group II and III by exchanging rows 1 and 3 and columns 1 and 3.
Each of the 48 group II magic squares transforms to one of the 48 group III.

#213        II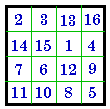

Group II

Exchange rows 1 & 3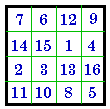

and col. 1 & 3 = # 808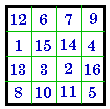

Group III

The same result is obtained by swapping rows and columns 2 and 4 instead of 1 and 3. This time a different magic square is obtained. From #213 it would be #361. 

Between Group I and Group III using quadrants to rows or rows to quadrants.
There are 48 magic squares of Group I and 48 of Group III. Each of these may be transformed from one type to a magic square of the other type by the following procedure. See A. and B. Use the same procedure but start at a different number in the quadrants (or rows) to get three more squares of the second type from the one original.

A. #183       III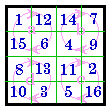	B. #171         I	Using #183  Group III for our original, construct #171 Group I by taking the four numbers in turn from each quadrant to form the four lines of # 171. C. and D. are the Dudeney patterns for the two magic squares. E. F. and G. illustrate how we can get three more pandiagonal magic squares from the same associated magic square, by simply starting at a different cell in the original.
C.  Type III	D. Type I	E. #204         I	F. #532         I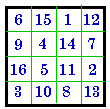	G. #560         I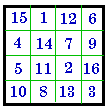
H. #171         I	J. #183         III	#808        III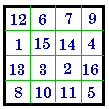	#698        III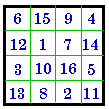	#361        III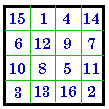

Those first 4 pandiagonal magic squares were obtained by starting with quadrant a. of the original associated magic square. By repeating the procedure but starting with quadrant b., then c. and finally d., 12 more pandiagonal magic squares are obtained. In fact we end up with the same set of 16 squares that were obtained by shifting rows and/or columns (proceeding section).

The bottom row illustrates how by reversing the process, four associated magic squares can be formed from one pandiagonal magic square.
Simply form the 4 quadrants of J. in turn from the 4 rows of H. to get back to the original associated square. The other 3 squares are formed by starting each quadrant from a different  position in the row. And by starting with a different quadrant we end up with 16 associated magic squares generated by 1 pandiagonal.
If we try the same procedure on any of the other 15 pandiagonal magic squares obtained above, we obtained disguised versions of the same 16 associated magic squares.

Another method (not shown). Exchange the last two columns, then exchange the last two rows, to convert magic squares between Group I and Group III.

Between Group IV and Groups V and VI interchanging rows (and columns)
There are 96 magic squares of Group IV. Each of these may be transformed to one of the 96 magic squares of Group V and to one of the 96 magic squares of Group VI. Here we use Group IV #251 as  an example.

#251     IV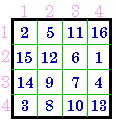	Group IV	exchange rows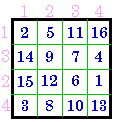	& columns = # 356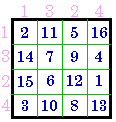	Group V
To transform from a Group IV to a Group V simply exchange rows 2 & 3 and columns 2 & 3. To transform from a Group IV to a Group VI simply exchange rows 2 & 4 and columns 2 & 4.		Exchange rows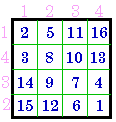	& columns = #227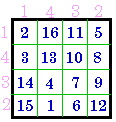	Group VI

Note that this transformation works in both directions i.e. also from V or VI to IV.
However, for Group VI,  it works only on the 96 that are semi-pandiagonal. On the 208 simple magic squares of order-VI, the result of  this transformation is only semi-magic.

Between Group VII and Groups VIII, IX and X
There are 56 magic squares of Group VII. Each of these may be transformed to magic squares of Groups VIII, IX or X by simple permutation of  rows and columns.

#717      VII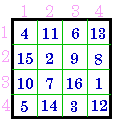	Group VII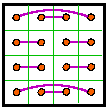	change row order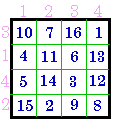	& columns = # 332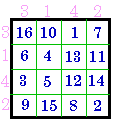	Group VIII
To transform from a Group VII to a Group VIII   change row and column order to 3, 1, 4, 2. To transform from a Group VII to a Group XI  change row and column order to 2, 1, 4, 3. To transform from a Group VII to a Group X  exchange rows 2 & 3 and columns 2 & 3. Note that for each of these four magic squares the Dudeney pattern is rotated 90 degrees from that shown by Dudeney (although in the case of #373, if the square is normalized the Dudeney pattern would be correctly orientated).		change row order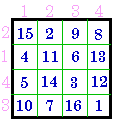	& columns = # 373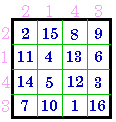	Group IX
		exchange rows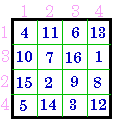	& columns = # 652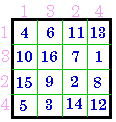	Group X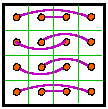

Between Group XI and Group XII
There are 8 magic square each of Groups XI and XII. Magic squares of one group may be transformed to magic squares of the other group by exchanging rows 2 & 4 and columns 2 & 4.

#374       XI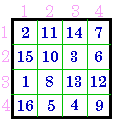

Group XI

exchange rows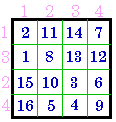

& columns = # 209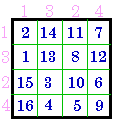

Group XII

Please send me Feedback about my Web site!

Last updated September 01, 2009
Harvey Heinz  harveyheinz@shaw.ca
Copyright © 1998, 2000 by Harvey D. Heinz