Self-similar Magic Squares

Any normal magic square may be transformed into another magic square by subtracting each number in turn from n² + 1. This process is referred to as complementing the magic square.
It is also referred to as 'complementary pair interchange' (CPI for short) because in effect you are interchanging the two numbers that together sum to n² + 1 ((R. S. Sery).
Under certain conditions the resulting magic square will be a reflected copy of the original magic square.

To illustrate using the Lo-shu magic square

This type of magic square was introduced on Mutsumi Suzuki’s Magic Squares page when he originally showed 6 order-5 magic squares of this type. He coined the name Self-similar magic squares.
Recently I revisited this page and discovered he had greatly expanded it, including 352 order-4 magic squares of this type.
Visit his large, comprehensive magic squares site from my links page.

On studying his page, I realized that the first group (his group A) of 48 order-4 magic squares are the only 48 associated magic squares of order-4.
On examining his order-5 self-similar magic squares, I find that they also are associated magic squares.
When I checked associated magic squares of other orders I found that in each case they were self similar.

Contents

Order-4 Associated         Used to demonstrate why associated magic squares are all self similar

Order-4 not associated   A class of 304 magic squares that are self-similar but not associated.

Order-4 not self-similar  An example showing why most magic squares are not self-similar.

Order-5 Associated        A sample lozenge associated magic square and its complement.

Order-6 not associated   An example that is horizontally self-similar.

Order-7 associated         A sample associated magic square and its complement.

Order-8 associated         A sample pandiagonal associated magic square and its complement.

Order-8 not associated  a bordered order-8 that is horizontally symmetrical and thus self-similar.

Order-9 associated         A sample lozenge associated magic square and its complement.

Higher dimensions           An order-3  magic cube and an order-3 magic tesseract.

Summery                         Conclusions and questions.

Order-4 Associated

1 8 12 13 14 11 7 2 15 10 6 3 4 5 9 16	This magic square is associated and semi-pandiagonal. It is #112 in Frénicle’s ordered list of the 880 order-4 magic squares and the first one that is associated. All order-4 associated magic squares are Dudeney type III .
16 9 5 4 3 6 10 15 2 7 11 14 13 12 8 1	This is the complementary copy of the above magic square. It is obtained by subtracting each number of the above square from 17. It is reflected horizontally and vertically from the original or to put it another way, it is rotated 180 degrees from the original.
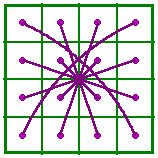	This pattern is constructed by joining integer pairs that sum to n2 + 1. The self-similar (complementary) magic square is constructed by simply exchanging the two numbers of each pair. Because it is completely symmetrical, the complementary square is self-similar and is reflected horizontally and vertically from the original.

Higher orders of associated magic squares have similar patterns, only with more lines. Note that every line passes through the center of the square. For this reason associated magic squares are also called symmetrical magic squares.

Order-4 not associated

The previous section mentioned that all associated magic squares, regardless of the order, have the self-similar property.

However, there is another type of order-4, and almost surely, other orders, that also have this property.
They are Dudeney’s type VI of which 96 are semi-pandiagonal and 208 are simple magic squares.

This is Frénicle’s index #1 , it’s complement and it's Dudeney pattern. It is a simple magic square.

1 2 15 16 12 14 3 5 13 7 10 4 8 11 6 9	16 15 2 1 5 3 14 12 4 10 7 13 9 6 11 8
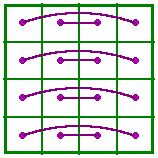Note that this complementary square needs only a horizontal reflection to make it identical to the original
1 12 14 7 13 8 2 11 4 9 15 6 16 5 3 10	16 5 3 10 4 9 15 6 13 8 2 11 1 12 14 7
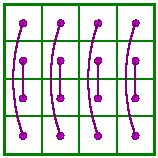This one is Frénicle # 182, it's complement and Dudeney pattern. It is semi-pandiagonal. This time the complementary square needs a vertical reflection to make it identical to the original. Comparing the complement pair patterns for the two squares makes it obvious why this is so. If magic squares of higher orders have complementary pair patterns equivalent to these, then those magic squares will also be self-similar. Whether these magic squares are semi-pandiagonal or simple seems to have no bearing on whether a horizontal or vertical reflection is required to match the complement to the original. The complements of both magic squares below require a horizontal reflection to match the original even though the squares are of different types.
Frénicle #53 simple 1 6 11 16 14 15 2 3 12 9 8 5 7 4 13 10	Frénicle #54 semi-pandiagonal 1 6 11 16 15 12 5 2 8 3 14 9 10 13 4 7

Credits regarding order-4
Mutsumi Suzuki lists 352 self-complementary magic squares of order-4.
His group A shows 48 magic squares that when complemented require a horizontal and a vertical reflection to match the original. These are the 48 Dudeney Type III associated semi-pandiagonal magic squares.

His group B lists 304 magic squares that when complemented require only a horizontal or a vertical reflection to match the original. These are the 96 Dudeney Type VI semi-pandiagonal magic squares and the 208 Dudeney Type VI simple magic squares.
Visit Mutsumi Suzuki’s large, comprehensive magic squares page from my links page.

Bernard Frénicle de Bessy published the 880 basic solutions for the order-4 magic squares in an indexed order in Des Quarrez Magiques. Acad. R. des Sciences 1693.

H. E. Dudeney published a classification of these 880 magic squares with the enumeration of each type in Amusements in Mathematics, Dover Publ., 1970, 0-486-20473-1. This is a reprint of a book first published in 1917.

Order-4 not self-similar

1 12 13 8 16 9 4 5 2 7 14 11 15 6 3 10

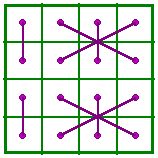This is Frénicle #181. Dudeney group XI. A look at the Dudeney pattern for this magic square confirms that the complementary pairs are not symmetrical across either the horizontal or the vertical center lines. This is the condition required for a magic square to be self-similar. For Order-4, groups III and VI are the only two types that have this characteristic.

Order-5 Associated

Order-6 not associated

1 28 27 10 9 36 35 26 25 12 11 2 3 22 21 16 15 34 33 24 23 14 13 4 20 6 8 29 31 17 19 5 7 30 32 18

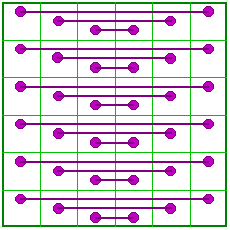This order-6 magic square is not associated but is symmetric across the vertical center line so produces a self-similar copy of itself. There are no associated pure magic squares of order 6.

Order-7 associated

Because this is an associated magic square, the complementary square must be both horizontally and vertically reflected to match the original.

Order-8 associated

This square is pandiagonal as well as being associated.

Order-8 not associated

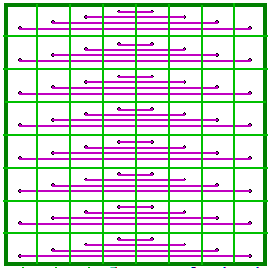
This magic square is not associated but symmetric across the vertical center, so produces a horizontally reflected version of itself.
It is also a bordered magic square. A double row of cells surrounds a 4 x 4 center magic square. Complementing only the center magic square or only the border cells will produce 2 variations. Rotating the center 4 x 4 either 90 or 270 degrees produces other variations.

17 23 9 53 12 56 42 48 5 50 22 46 19 43 15 60 13 64 38 36 29 27 1 52 47 3 35 31 34 30 62 18 7 4 25 37 28 40 61 58 63 59 32 26 39 33 6 2 57 16 44 20 45 21 49 8 51 41 55 11 54 10 24 14

Order-9 associated

71 64 69 8 1 6 53 46 51 66 68 70 3 5 7 48 50 52 67 72 65 4 9 2 49 54 47 26 19 24 44 37 42 62 55 60 21 23 25 39 41 43 57 59 61 22 27 20 40 45 38 58 63 56 35 28 33 80 73 78 17 10 15 30 32 34 75 77 79 12 14 16 31 36 29 76 81 74 13 18 11

65 72 67 2 9 4 47 54 49 70 68 66 7 5 3 52 50 48 69 64 71 6 1 8 51 46 53 20 27 22 38 45 40 56 63 58 25 23 21 43 41 39 61 59 57 24 19 26 42 37 44 60 55 62 29 36 31 74 81 76 11 18 13 34 32 30 79 77 75 16 14 12 33 28 35 78 73 80 15 10 17

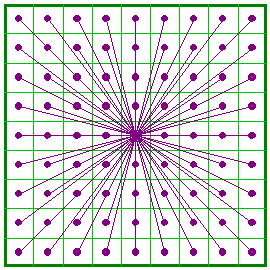
This associated magic square is also composite. It consists of nine order-3 associated magic squares themselves arranged as an order-3 magic square. If each number in this order-9 square is exchanged with it's complement as per the Dudeney pattern, the result is the same magic square rotated 180 degrees. In addition, each of the nine order-3 magic squares can be converted to its complement (itself but rotated 180 degrees) by subtracting each number from the sum of the first and last number in that magic square. This in turn will produce another order-9 associated magic square (shown at left) which is also self-similar. Any order-3 or combinations of order-3 may be rotated to get variations in the order-9 magic square. Notice that for simplicity, some lines in the pattern (above) are covered up by others. The center horizontal line, for example, actually consists of four pairs.

Higher Dimensions

The self-similar feature also works for associated magic cubes and tesseracts. I assume it works for the higher dimensions as well.
Shown here is an order-3 cube and an order-3 tesseract, both are complements of those shown on my John Hendricks page. Refer to that page for more information on these figures.
Just as the 1 order-3 magic square is associated, so also are the 4 basic magic cubes and the 58 basic magic tesseracts.

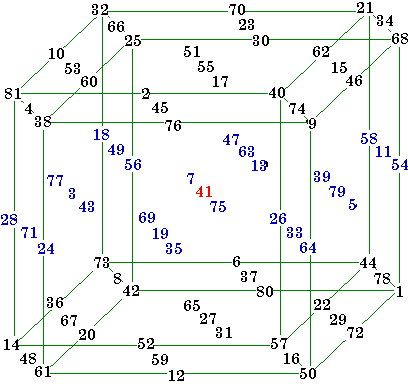The magic cube has 13 complementary pairs with the two members on opposite sides of the central number 14. This self-similar figure is one of the 47 equivalents to the cube on Hendricks page.

The magic tesseract shown above has 40 complementary pairs around the central number 41. Two such pairs are 32, 50 and 18,64. This self-similar figure is one of the 383 equivalents to the tesseract on Hendricks page.

Summery

All associated magic squares (and higher dimensions) have the self-similar property. i.e. if each number in the square is subtracted from the sum of the first and last number in the series, the resulting magic square is a duplicate of the original but rotated 180 degrees.
This process  of  complementing all numbers may be referred to as complementary pair interchange (CPI).

Any non-associated magic squares that have complementary pairs that are symmetric across either the horizontal or the vertical center line produce self-similar copies that are either horizontally or vertically reflections of themselves.
I have shown such a pattern (above) for orders 4 and 6.

All order-4 associated magic squares are semi-pandiagonal. Are ALL associated magic squares semi-pandiagonal?

Please send me Feedback about my Web site!

Harvey Heinz   harveyheinz@shaw.ca
This page last updated February 28, 2009
Copyright © May, 2000 by Harvey D. Heinz