 |
 |
 |
 |
 |
Order-7 with Diamond Inlays |
This magic square contains an order-3 and an order-4 magic diamond. |
Order-7 with Square Inlays |
Orders 3and 4 interleaved magic squares and other properties. |
Order-9 with Diamond Inlays |
Inlaid are an order-7 and an order-5 and also an order-3 diamond. |
Order-14 Ornamental |
Included here are orders 3 and 5 magic squares and magic diamonds. |
Order-15 Overlapping |
A total of 15 magic squares in one. Orders 4, 7, 8, and 15. |
Two related ten-in one |
One has 10 magic squares with bent diagonals & 1 has 5 pandiagonals. |
Order-15 Composite |
Composed of nine order-5 magic squares, each with a magic diamond. |
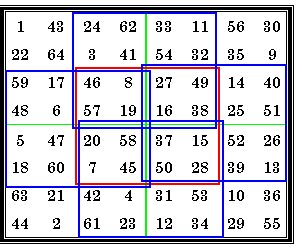
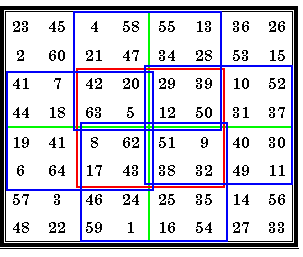
Order-3 Magic Cube |
A normal order-3 magic cube using numbers 1 - 27. |
Pan-3-agonal magic cube |
This order-4 magic cube has all broken pan-triagonals summing correctly. |
Order-3 Magic Tesseract |
This magic hypercube is 4-dimensional and uses numbers 1 to 81. |
Order-8 Inlaid Magic Cube |
Contains an order-4 pan-triagonal cube and 12 pandiagonal magic squares |
Inlaid Magic Tesseract |
Announcement of world's first inlaid magic tesseract. Oct. 15/99. |
Order-9 Bimagic Square |
A bimagic square by David Collison and a new type by John Hendricks. |
About John Hendricks |
A brief autobiography and outline of accomplishments in this field. |
JohnHendricksMath |
John Hendricks original web page (now maintained by H. Heinz) |
![]()
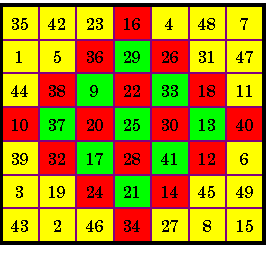
Order-7 Magic Square S = 175
Order-4 Magic Diamond S = 100
Order-3 Magic Diamond S = 75
From The Magic Square Course, title page for chap. XII
![]()
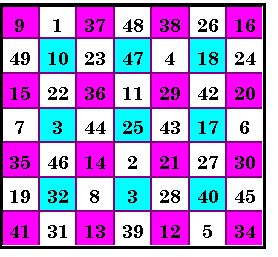 Order-7 Magic Square
sum = 175
Order-7 Magic Square
sum = 175
Order-4 (pink) Magic Square sum = 100
Order-3 (blue) Magic Square sum = 75
Corners of each of these 3 magic squares sum to 100
Uncolored squares sum as follows (in any direction):
lines of 2 cells = 50
lines of 3 cells = 75
lines of 4 cells = 100
lines of 6 cells = 150
From The Magic Square Course, page 46
![]()
 S9 = 369
S9 = 369
S7 = 287
S5 = 205
S3 = 123
This inlay may be used in place of the above order-5 inlay
|
42 |
34 |
49 |
30 |
50 |
|
22 |
39 |
61 |
23 |
60 |
|
51 |
25 |
41 |
57 |
31 |
|
58 |
59 |
21 |
43 |
24 |
|
32 |
48 |
33 |
52 |
40 |
From The Magic Square Course, page 191
TOP Sub-square
Diamond
Bottom Sub-square
Diamond
S5 =
615
S4 = 100
S5 =
370 S4
= 688
S3 = 369
S3 =
516
S3 =
222 S3
= 75
For a total of 9 magic squares. By John Hendricks (unpublished)
MAGIC SUMS Lower left
& upper right Upper
left & lower right
S15 = 1695
2 x S7 = 791 (Pandiagonal)
2 x S8 = 904
10 x S4 = 452
For a total of fifteen Magic squares
From The Magic Square Course, page 232
![]()
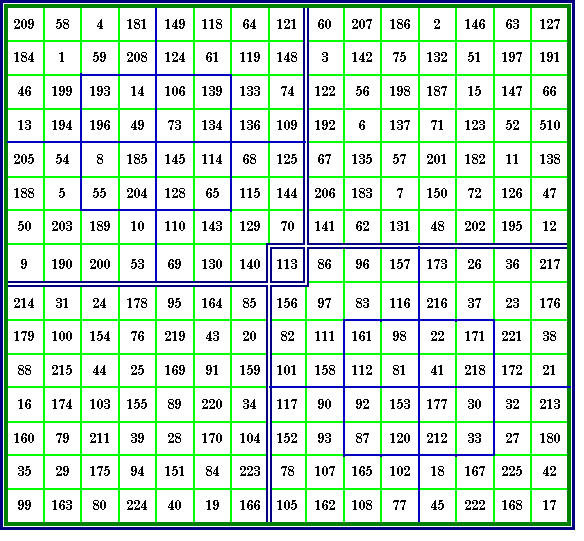
 |
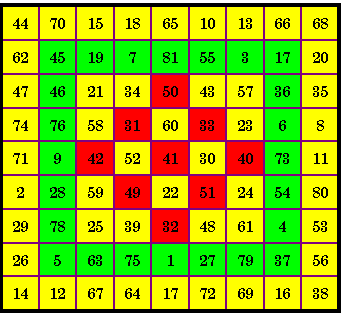
This order-8 magic square contains four order-4 magic squares in the quadrants and one
order-4 in the center. It contains four more order-4 magic squares starting with the top left hand corner at 24, 59, 27 and 20 (outlined in blue). S4 = 130 S8 = 260 All ten of these magic squares have the additional feature that each of the four bent
diagonals also sum correctly. Two of these bent diagonals in the top left hand order-4 are
1 + 64 + 3 + 62 and 1 + 64 + 17 + 48. Figure 12a from Inlaid Magic Squares & Cubes, page 18 |
 |
This order-8 magic square is pandiagonal. The four order-4 magic squares in the
quadrants are also pandiagonal. The order-4 in the center and the four order-4 outlined in blue are regular magic squares.
Figure 11h from Inlaid Magic Squares & Cubes (revised), page 17 |
![]()
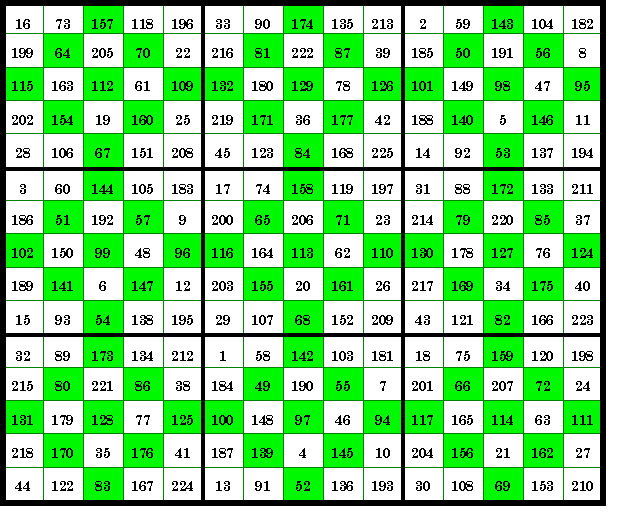
| S of Order-5 squares
|
S of Order-3 diamonds
|
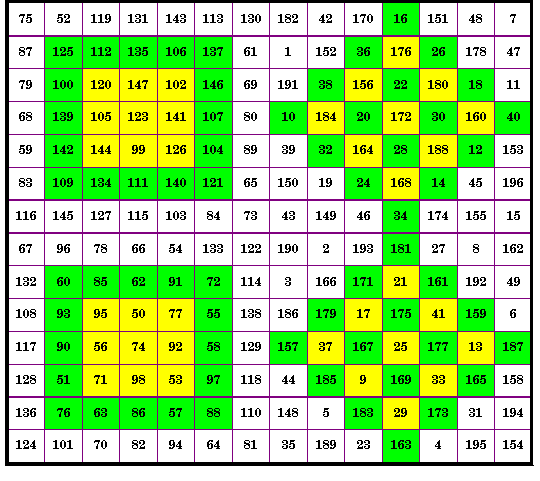
This order-15 magic square consists of 9 order-5 magic
squares, each with an order-3 inlaid diamond magic square. As is common with composite
magic squares, the magic sums of the order-5 squares themselves form an order-3 magic
square with the constant 1695. From The Magic Square Course, page 244 |
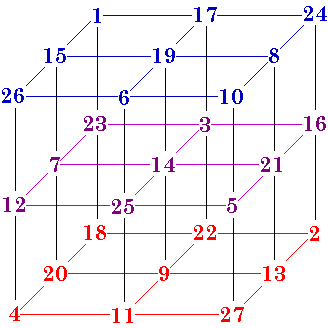 9 rows, such as 1 - 17 - 24, sum to 42.
9 rows, such as 1 - 17 - 24, sum to 42.
9 columns, such as 1 - 15 - 26, sum to 42.
9 Pillars, such as 1 - 23 - 18, sum to 42.
4 triagonals, such as 26 - 14 - 2 sum to 42.
Some of the squares may have diagonals summing to 42, but this is not a requirement. In fact, order-8 is the smallest cube for which it is possible for all the diagonals to sum correctly.
What is required is that the 4 triagonals or 3-agonals, such as 1 - 14 - 27 sum to 42.
There are 4 different basic pure (using numbers 1 to 27) magic cubes. Each of these have 48 equivalents due to rotations and/or reflections.
From The Magic Square Course, page 329.
Just as the one order-3 magic square is associated, so also are the four order-3 magic
cubes. Because they are associated, all are also self-similar. That is, when each number
is subtracted from 28 the result is a reflection of itself.
See my Self-similar Magic Squares.
![]()
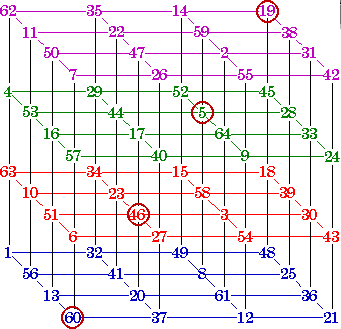 16 rows sum to 130
16 rows sum to 130
16 columns sum to 130
16 pillars sum to 130
Four 3-dimensional diagonals sum to 130.
All broken 3-agonals parallel to the 4 main triagonals also sum to 130.
This is the equivalent to the pandiagonal Magic Square.
Because it is pandiagonal, any face may be moved to the opposite side, thus
creating a new pan-3-agonal magic cube.
The numbers circled in red show one of the 4 main triagonals.
In an order-4 cube it is impossible for all the diagonals parallel to the faces to be
magic.
John Hendricks coined the term pan-3-agonal for the broken space 3- agonals.
There are 7680 pan-3-agonal magic cubes of order-4. The total number of Order-4 magic
cubes is not known.
From The Magic Square Course, page 384
This also appeared in The Journal of Recreational Mathematics, 5(1) p. 51-52.
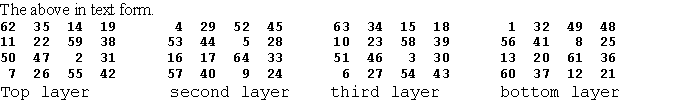
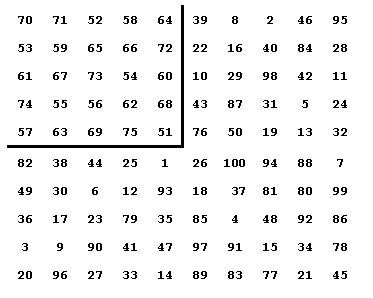
 This order-3 hypercube of four dimensions is shown in two
dimensions using lines to depict the outer dimensions only. The colored numbers here show
the middle cube in the horizontal plane. There are three cubes also in each of the other
three planes.
This order-3 hypercube of four dimensions is shown in two
dimensions using lines to depict the outer dimensions only. The colored numbers here show
the middle cube in the horizontal plane. There are three cubes also in each of the other
three planes.
27 rows, such as 50 - 12 - 61, sum to 123.
27 columns, such as 50 - 72 - 1, sum to 123.
27 pillars, such as 50 - 64 - 9, sum to 123.
27 files, such as 50 - 16 - 57, sum to 123.
8 quadragonals, such as 1 - 41 - 81 sum to 123.
Some of the squares may have diagonals summing to 123 and some of the cubes may have
triagonals summing to 123. These are not requirements of a magic tesseract just as a magic
cube is not required to have the planar square diagonals summing to 42.
What is required is that the 8 quadragonals or 4-agonals, such as 50 - 41 - 32 sum to 123.
There are 58 different basic pure (using numbers 1 to 81) magic tesseracts. Each of
these have 384 equivalents due to rotations and/or reflections.
From The Magic Square Course, page 470-491 (which shows all 58 order-3).
Just as the one order-3 magic square and the four order-3 magic cubes are associated, so also are the 58 order-3 magic tesseracts. Because they are associated, all are also self-similar. That is, when each number is subtracted from 82 (i.e. complimented), the result is a reflection of itself and is one of the 384 aspects of this figure. See my Self-similar Magic Squares.
![]()
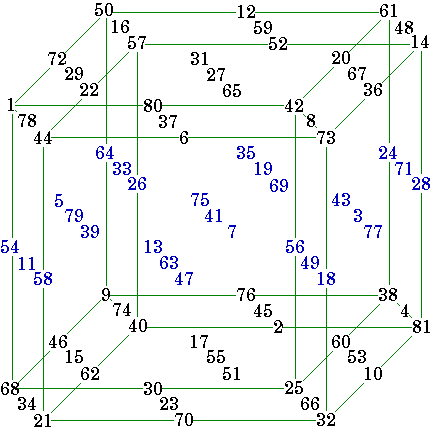
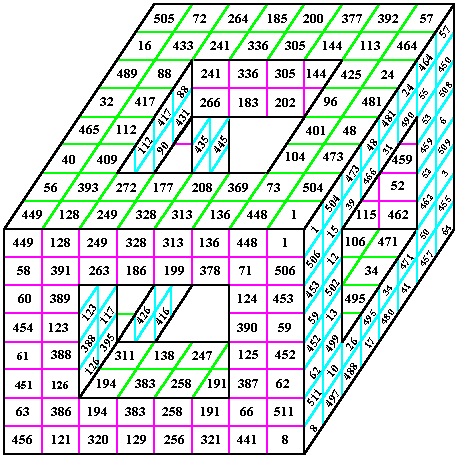 Here is the shell for an order-8 magic cube with an inlaid
order-4 magic cube.
Here is the shell for an order-8 magic cube with an inlaid
order-4 magic cube.
Each of the six windows shown holds two order-4 pandiagonal magic squares.
The inner order-4 cube is pantriagonal meaning that all broken triagonal pairs sum correctly to 1026.
The order-8 cube uses the numbers from 1 to 83 and has the magic sum of 2052.
Note that it is not a requirement that planar diagonals sum correctly for a cube to be considered magic, although it is possible for an order-8 (the smallest order cube) to have this feature .
The author reasons that there are 2,717,908,992 variations of this one cube, obtainable by rotations, reflections and transformations of the components.
Here are the individual layers of the cube. Note that in most cases they are only semi-magic (the planar diagonals will not sum correctly).




From the above eight horizontal planes, the 16 vertical planes and the four triagonals can be assembled.
From The Magic Square Course, pp. 419 - 431
 |
|
Discovered during the spring of 1999, was a new method of making magic squares of order 2k. An example shown top left is a tenth-order magic square which sums 505 in rows columns and diagonals. In the second quadrant, you will find inlaid a 5th-order magic square which sums 315. Inlaid squares and various methods abound, so this simply adds another method into the system. MAJOR ANNOUNCEMENT The technique mentioned above, can be extended to three and four-dimensional space and higher. A magic tesseract of order six, with an Inlaid magic tesseract of order three has been made. It contains the numbers from 1 to 1296 and sums 3,891 in the required 872 different ways. This is the world’s first magic tesseract of order six. The inlaid magic tesseract of order three sums 1,824, in the required 116 different ways. This becomes the world’s first inlaid magic tesseract. The new method for magic squares will be taken into account in the upcoming Second Edition of Inlaid Magic Squares and Cubes, which is unscheduled at the moment. |
|
 |
|
| John R. Hendricks | |
![]()
HENDRICKS’ BIMAGIC SQUARE OF ORDER NINE
Bimagic means that you can sum the numbers as they are, or you can square them all first and then sum them. Either way, the square is magic.
David M. Collison, first discovered bimagic squares of order nine. An example is shown in Figure 1. He died before he could reveal just how he made it and mathematicians are still searching to find his method of construction.
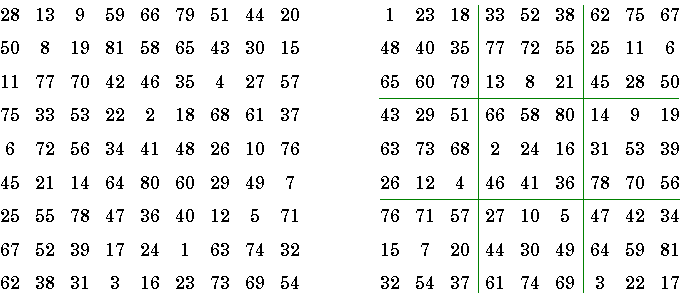
Figure 1. Collison’s regular, Figure
2. Hendricks’ newly
or associated bimagic square. created
bimagic variety.
In Figure 2, the square is partitioned into nine zones. These are not magic sub—squares — just zones. Each zone of nine elements sums 369, as does’ each row, each column and both diagonals. If you square all the numbers and then add them up, you will find that each zone sums 20,049, as does each’ row, column and both diagonals.

With the new bimagic square, you can translocate any 3 by 9 rectangle of numbers to the opposite side of the square, as shown above, and a new bimagic square will emerge.
John R. Hendricks
Victoria, BC, Canada
25 November 1999
![]()
Mr. Hendricks worked for the Canadian Meteorological Service for 33 years, and retired in 1984. Early in his career, he was a meteorological instructor for the N.A.T.O. Training Program. Later, he was a weather forecaster at various locations across Canada. Throughout his career, he was also known for his contributions to statistics and climatological statistics.
While employed, he also participated in volunteer service groups, including The Monarchist League of Canada and he was the founding President, Manitoba Provincial Council, The Duke of Edinburgh's Award in Canada. He was a recipient of the Canada 125 medal for his volunteer work.
Following his career in meteorology, he gave many public lectures on magic squares and cubes in schools and at in-service teacher's conventions both in Canada and in the northern United States. He developed a course on magic squares and cubes for the mathematically inclined students at Acadia Junior High School in Winnipeg for seven years. The resulting text book of over 550 8.5" x 11" pages was never published. He delivered half a dozen colloquia to professors of mathematics on the subject and in geometry and statistics, as well. He assisted in the Shad Valley program for several years.
John Hendricks started collecting magic squares and cubes when he was 13 years old. This became a hobby with him and sometimes even an obsession. He never really thought that he would ever expand the knowledge in this field. But soon, he became the first person in the world to successfully make four, five and six-dimensional models of magic hypercubes, and publish them. He has written prolifically on the subject in the Journal of Recreational Mathematics. He has also extended the knowledge of magic squares and cubes, especially the ornate and embedded varieties.
John R. Hendricks, Bimagic Squares of Order-9, Dec.
1999, 14 pages 8 ½ x 11+covers 0-9684700-6-8
John R. Hendricks, Perfect n-Dimensional Hypercubes of Order 2n, May
1999, 36 pages 8 ½ x 11, 0-9684700-4-1
Equations are shown for the first
perfect Tesseract and Basic programs for orders 4 -6.
John R. Hendricks, Inlaid Magic Squares and Cubes, Feb.
1999, 214 pages 8 ½ x 11, 0-9684700-1-7
Equations, examples, programs and a list of
the 46 articles (mostly magic square related) he has had published in journals.
John R. Hendricks, All Third Order Magic Tesseracts, Feb. 1999,
36 pages 8 ½ x 11, 0-9684700-2-5
John R. Hendricks, Magic Squares to Tesseracts by
Computer, 1998, 212 pages 8 ½ x 11, 0-9684700-0-9
Equations, examples, and 3 appendices dealing
with rotations/reflections, magic squares of order 4k+2, and programs.
| Update: January 30, 2004 Due to ill health and depleted stock, John's books are no longer available. He no longer has an e-mail address. Sadly, John Hendricks passed away on July 7, 2007. I am still maintaining (Sept. 1, 2009) his original web site here. |
![]()
Please send me Feedback about my Web
site!![]()

![]()

![]()
Last updated
September 01, 2009
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998, 1999,2000 by Harvey D. Heinz