 |
 |
 |
 |
 |
|
|
|
|
|
|
 |
 On this page I show photographs
of handicraft projects made using magic squares, magic stars and related subjects as the
theme.It is a rewarding experience to hold, for example, an actual 3 dimensional model of a magic star or cube, instead of simply viewing a 2 dimensional version of it on paper. Unfortunately, a photograph simply reverses the process, and we are once again viewing a 2 dimensional version of the object. |
CONTENTS
A Cross-stitched Magic Square |
of order-5 (but lots of combinations). |
A Cross-stitched Magic Star |
of order-6. Points also are magic. |
A Pandiagonal Torus |
Any pandiagonal magic square may be considered as being on the surface of a torus in stead of a plane. |
Order-4 Magic Square |
constructed with wooden blocks and dowels. |
A Wooden Magic Cube |
of order-3. Magic lines shown with dowels. |
A Wooden 3-D Magic Star |
An 8-point star with 12 lines of 3 numbers sum to 27. |
A Wooden 3-D Magic Star- 2 |
As above, but 3 missing numbers inserted to now give 22 lines summing correctly. |
A Number Pattern |
12 = 3 x 4, 56 = 7 x 8, 9 is not equal to 0. |
Order-3 in Cross-Stitch |
A magic square rainbow. |
A 3 dimensional magic square |
A order-5 pandiagonal associated magic square constructed with wooden dowels and metal washers. |
Six magic cubes in One |
A wooden block and dowel construction of an order 4 pantriagonal magic cube. The numbers on each face of the cubelets represent a different magic cube. |
A Cross-stitch Quadrant Magic Square |
My order -13 Quadrant magic square has 14 patterns correct in all 4 quadrants. |
Order-3, Dimensions 2, 3, and 4 |
In cross-stitch. The Lho-shu order-3 square, order-3 cube # 3, and order-3 tesseract # 5 (Hendricks # 1) |
 |
This pandiagonal magic square required the use of negative numbers so the
constant could be made equal to 40. It was a gift to my son for his 40th birthday and was
presented to him in a plastic desk stand. On the back of the pattern are diagrams showing how there are at least 428 different ways to form the number 40 using arrangements of 5 numbers. See How many groups = 65? for more information on this type of magic square. The cross-stitched magic square is 4.5 inches by 4.5 inches, and has 67 by 67 cross-stitches. (There are also red shadow back stitches on the digits which do not show in the picture.) |
 |
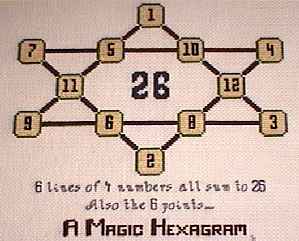This cross-stitched magic star is a reflected version of index number 16
(of the 80 basic solutions). The actual size of this project is 8 inches by 7 inches. The size of each of the 12 cells is 3/4 inch. Projects like this are a nice break from sitting in front of the computer. The squashed shape is a result of lines such as 1 - 10 - 12 -3 having to be on a 45 degree angle when the fabric has square stitches. |
 |
When explaining the system of broken diagonal pairs in a pandiagonal magic
square, the magic square is often explained as being part of an infinite plane. Sometimes the reader is advised to imagine the edges of the magic square folding back and joining the opposite edge. In effect, the magic square is on the surface of a torus instead of a plane. Pictured here is a crude model of such a pandiagonal magic square. Any of the 25 numbers may be considered the first number of the first row. Then the square is built up by simply following the lines around the torus. See Unusual Magic Squares for more information. |
 |
This is a 3-D model of an order-4 pandiagonal magic square. The wooden
blocks are 3/4 inch, the dowels, 1/8 inch. 1 15 4 14 |
 |
An order-3 magic cube. Size is 4.5" x 4.5" x 4.5"
Magic sum is 42 on all the 9 rows, 9 columns, 9 pillars and 4 triagonals. |
 |
This is a model of the 3-D magic star discovered by Aale de Winkel
and myself in May, 1999. It has 12 lines of 3 numbers all summing to 27, forming a star
with 8 points. The arrangement may be considered as 2 triangular based pyramids pointing in opposite
directions and intersecting at the midpoints of their sides. |
 |
Another view of the 3_D magic star. However, here the line formed by the 3
unused numbers (3, 9, 15 which also sum to 27) are incorporated into the star figure. The
magic star, on it's own has 12 lines summing to 27. Except for the 1 line consisting of the 3, 9 and 15, I do not show these extra lines with dowels. Two of them however, are formed by the rubber bands holding the 3, 9 15 line in place. An apology. I made the mistake of varnishing these models. When I tried to illuminate them for pictures, I found the reflection blocked out the numbers, so I had to photograph them with minimal lighting. |
See 3-Dimensional Magic Stars for more information.
This cross-stitch pattern shows on my 19" monitor (1024 x 768 pixals) as almost
actual size (14 squares/inch).
 |
Colors didn't reproduce too good in this image, but you get the idea. |
 |
The idea for this novel magic square was sent to me by Craig Knecht on
June 5, 2001. This is an order-5 pandiagonal associated magic square. The 325 metal washers give this model a weight of almost 2 pounds. |
|
This model is constructed using 64 3/4" wooden blocks and connected by 1/8" hardwood dowels showing rows, columns, pillars and triagonals. Numbers used are 1 to 384, which is 43 times 6.
The six faces of each cubelet are painted six different colors. The 64 faces of each color form a magic cube with constants ranging from 760 to 780. All 6 cubes have the same characteristics. They are:
The cube is pantriagonal, so each cube has 112 correct lines. All 2x2 square arrays (including wrap-around) in each cube also add to the constant, giving another 192 combinations per cube..
 |
Magic constants: White = 760, Blue = 764, Red = 768,
This model was completed on July 28, 2002 |
This is the cube with the white faces. The magic constant is 760.
White S = 760
Top
Top – 1 Bottom + 1 Bottom
1
355
217
187
367
37
151
205
109
247
325
79
283
121
67
289
373
31
157
199
19
337
235
169
265
139
49
307
103
253
319
85
55
301
271
133
313
91
97
259
163
193
379
25
229
175
13
343
331 73
115
241
61
295
277
127
223
181
7
349
145
211
361
43
Quadrant magic squares are discussed here. The complement of this square is on this page.
| Here are pictures of a cross-stitch project I
started July 13/03 and completed on Dec. 1/03. It is a complement square to the one shown above. For those who are interested in cross-stitch, it is on |
 |
 |
 |
This pattern is cross-stitched on 18-count (18 squares to
the inch) Aida light mocha colored fabric. The design was started about July 1, 2007, and the stitching was finished (with interruptions) on Jan. 28, 2008 The magic square is the only basic square of this order. The magic cube is index number 3. And the magic tesseract is index number 5. It is the first tesseract John Hendricks constructed with his newly invented tesseract pattern (in 1950), so by his numbering it is # 1. Click on the image for an enlargement. |
Please send me Feedback about my Web
site!
Last updated
February 15, 2008
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998, 1999 by Harvey D. Heinz
