 |
 |
 |
 |
 |
The example on this page is used to show some of the number
patterns that sum to the magic constant.
Also some definitions to help you understand my explanation of this square.
See how five numbers can combine in 1128 ways to sum to 65.
| July 31/99 Not so! |
See the addendum now at the end of this
page, which explains a very big error in my count! I have chosen to leave the original page as is to better explain how wrap-around can cause apparently different patterns. |
Pandiagonal
Associative
Compact Self-similar Wrap-around
5 Symmetrical cell pairs
8
Non-symmetrical patterns
![]()
1 |
15 |
24 |
8 |
17 |
23 |
7 |
16 |
5 |
14 |
20 |
4 |
13 |
22 |
6 |
12 |
21 |
10 |
19 |
3 |
9 |
18 |
2 |
11 |
25 |
| Combination | # | Example | Example | |
| Rows | 5 | 1, 15, 24, 8, 17 | ||
| columns | 5 | 1, 23, 20, 12, 9 | ||
| diagonals | 10 | 1, 7, 13, 19, 25 | includes broken diagonal pairs | 15, 16, 22, 3, 9 |
| corners of 3 x 3 squares + center | 25 | 1, 24, 7, 20, 13 | including wrap-around | 12, 10, 18, 1, 24 |
| corners of 5 x 5 squares + center | 25 | 1, 17, 13, 9, 25 | including wrap-around | 23, 14, 10, 1, 17 |
| corners of 2 x 2 rhombics + center | 25 | 23, 15, 7, 4, 16 | including wrap-around | 11, 3, 25, 17, 9 |
| corners of 3 x 3 rhombics + center | 25 | 20, 24, 13, 2, 6 | including wrap-around | 2, 6, 25, 14, 18 |
| corners of 4 x 4 rhombics + center | 25 | all are wrap-around | 1, 22, 8, 19, 15 | |
| corners of 5 x 5 rhombics + center | 25 | all are wrap-around | 7, 20, 23, 1, 14 | |
| Plus | 58 | combinations of any 2 symmetrical cell pairs plus the center cell. (see diagrams below) | 1, 15, 13, 11, 25 wrap-around doesn’t work | |
| Plus | 900 | combinations of 8 non-symmetrical patterns (see diagrams below) | 1, 8, 17, 14, 25 15, 17, 1, 23, 9 | |
Total combinations of five cell patterns summing to 65 = 1128
Do you arrive at the same total? (Note:
see addendum for correct total)
1 |
15 |
24 |
8 |
17 |
23 |
7 |
16 |
5 |
14 |
20 |
4 |
13 |
22 |
6 |
12 |
21 |
10 |
19 |
3 |
9 |
18 |
2 |
11 |
25 |
Pandiagonal Magic
Square
Also known as Diabolic, Nasic, Continuous, Indian, Jaina or Perfect
M.S. To be pandiagonal, the broken diagonal pairs must also sum to the magic
constant. This is considered the top class of magic squares. Some pandiagonal magic
squares are also associative (order 5 & higher) . Because of the vast number of
combinations possible, individual magic squares may contain other unique features that
make them more magic.
There is only 1 basic order 3 magic square and it is not pandiagonal.
Of the 880 basic order 4 magic squares, only 48 are pandiagonal and none of these
are associative.
Order 5 has 3600 basic pandiagonal magic squares (Only 36 essentially different).
Order 7 has 678,222,720 basic pandiagonal magic squares. (38,102,400 regular plus
640,120,320 irregular pan-magic squares). See Benson & Jacoby, New Recreations With
Magic Squares, Dover Publ., 1976.
Order 8 has more then 6.5 billion pandiagonal magic squares.
Associated M.S.
A magic square where all pairs of cells diametrically equidistant from
the center of the square equal the sum of the first and last terms of the series, or n2
+ 1. Also called Symmetrical or Regular. The center cell of odd order
associated magic squares is always equal to the middle number of the series. Therefore the
sum of each pair is equal to 2 times the center cell and the sum of any 2 symmetrical
pairs plus the center cell is equal to the constant. This permits a great many
combinations (the order 5 square above has 58 of this type).
In an even order magic square, the sum of any 2 symmetrical pairs will equal the
constant.
There are NO singly-even Associated magic squares.
The one order-3 magic square is associative.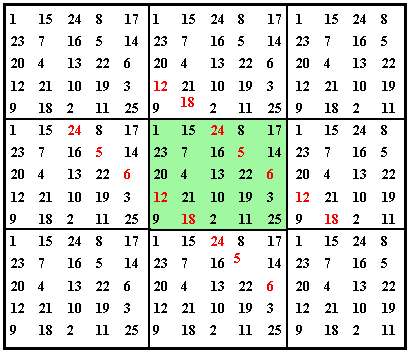
Compact means corner and center cells of all small squares (including rhombics) sum to the constant. This is an extension of the formal definition of Compact as written for double even order pandiagonal magic squares. See Glossary.
Self-similar means that when each number is changed to its complement (i.e. subtracted from n+1), an identical magic square is formed but rotated 180 degrees. This term was coined by Mr. Mutsumi Suzuki who discovered six such squares. See his excellent site at http://www.pse.che.tohoku.ac.jp/~msuzuki/ (Sorry, this is no longer available on the Internet).
Wrap-around means when you go off of one edge, continue (wrap-around) to the corresponding cell on the opposite edge. The easiest way to accomplish this is to lay out the magic square in a repeating pattern on the plane as shown to the right. Then any 5 x 5 array is an equivalent pan-diagonal magic square. So, to complete a line, you can just keep going in the same direction. The red cell values illustrate wrap-around when applied to a broken diagonal pair. Wrap-around works only with pan-diagonal magic squares.
The Five Symmetrical cell pairs
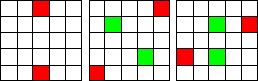 |
Note that some of these combinations are duplicates of the basic patterns counted at the start. Example; if the 2 patterns in the center diagram are lined up, this combination constitutes a main diagonal which has already been counted. |
Non-symmetric
Patterns
The seven patterns on the left (below) each appear 25 times
because of wrap around and 4 times due to rotation ( i.e. 7 x 25 x 4 = 700).
They are
symmetrical about a horizontal, vertical or diagonal axis and so cannot be reflected for
unique solutions.
That pattern 1 will always be magic in an order-5 pandiagonal magic square, if
it is rotated so the 3 adjacent cells are in any of the 4 corners was proven by
Rosser and Walker in 1939 [1].

The pattern on the right is not symmetrical around a vertical, horizontal,
or diagonal axis, so appears 25 times because of wrap around, 4 times due to rotation and
2 times because of reflection (i.e. 25 x 4 x 2 = 200).
Starting a given pattern on a different cell, in combination with a rotation or a
reflection, may result in the same 5 cells being used. Example, start the first pattern
with 9, 23, 1, 15, 17. Now rotate the pattern 90 degrees clockwise and start with 15,17,
1, 23, 9. Both combinations use the same 5 cells, but in a different arrangement. I
consider them different combinations.
Of course, we could say the same about the use of wrap-around when computing the number of
combinations for rows, columns and the diagonals. However, by convention, these extra
combinations are not counted.
[1] R. Rosser and R.J Walker, The Algebraic Theory of Diabolic Magic Squares, Duke Mathematical Journal, Vol. 5, No, 4, Dec. 1939 pp 705-728 (p.717)
![]()
On June 28/99, I received an e-mail from Aale de Winkel advising me that he thought non-symmetric pattern 1, above, was actually equivalent to the wrap-around 2 by 2 rhombic, and patterns 2 and 8 were equivalent to the wrap-around 2 by 2 square.
Subsequent investigation on my part confirmed these equivalents, and also
that four of the other five patterns are also equivalent to symmetric patterns
already counted.
1. is equivalent to wrap-around 2 by 2 rhombic ( now called plusmagic ---
see Quadrant Magic Squares)
2. is equivalent to wrap-around 2 by 2 square ( now called crosmagic)
3. is equivalent to wrap-around 3 by 3 rhombic corners.
4. is equivalent to wrap-around 5 by 5 square corners.
5. is just a reflected 4. (another goof!).
6. is unique, so add 100 combinations to the total.
7. is equivalent to wrap-around 5 by 5 square corners.
8. is equivalent to wrap-around 2 by 2 square
The three diagrams below demonstrate the equivalence of the 2 x 2
rhombic (plusmagic) and non-symmetric pattern 1.
Diagram A shows pattern 1 within the magic square and
the plusmagic with two cells outside of the square. diagrams B and C
show the patterns shifted down and to the right. In each of these cases, the plusmagic
pattern is within the square and two cells of the pattern 1 outside.
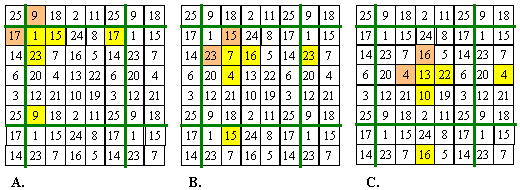
Yet to be determined. Should the rotated non-symmetric
patterns be counted and included in the total?
For now, let us say that there are 328 different combinations!
By the way. There are 1394 sets of 5 numbers, from the first 25 consecutive numbers, that
sum to 65!
![]()

Please send me Feedback about my Web
site!![]()

![]()
![]()
Last updated
05/10/2009
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998 by Harvey D. Heinz