Trump - Ultra magic

Ultra Magic squares – Walter Trump

In 2002 Walter Trump investigated unusual magic squares which he decided to call ultra-magic. Most of the wording, and all of the examples shown here is from material condensed from several emails and attached spreadsheets sent to me in February 2002.
Some of this work was in collaboration with George Chen.

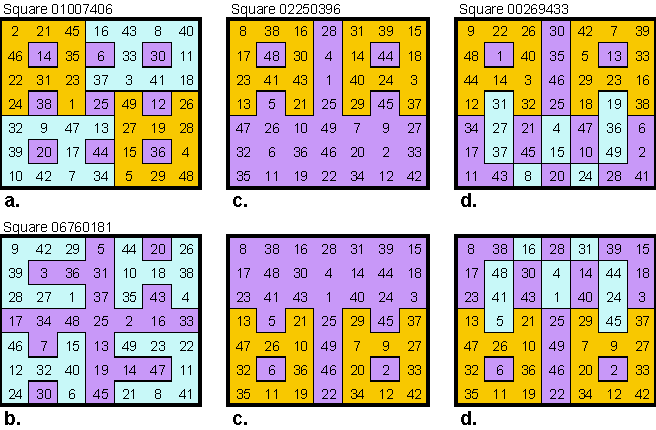
Square a. is one of 17 order-7 Walter found that are all pandiagonal, center symmetrical (=associative), and contain two magic 3x3 arrays

These are squares 04347674 and 06969925 from Trump's database of 20,190,684 squares.

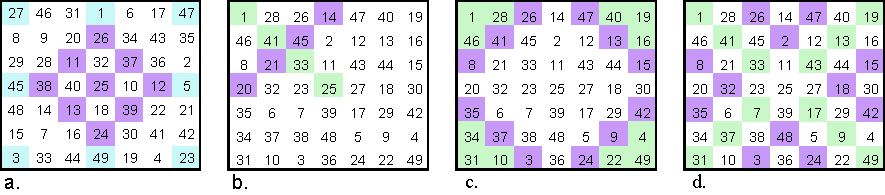
Squares b., c., and d. are 1 of 11 magic squares of order 7 with following features

pandiagonal
center symmetric (associative)
bent main-diagonals sum up to 7 x 25 (= magic sum)
in each 4x4 quadrant (overlapping) the diagonals sum up to 4x25 (square b.)
Several sets of three cells sum up to 3 x 25 (squares c. and d.)

There are 96 magic squares of order 7 with the following features

center symmetric (associative)
pandiagonal
the sum of the squares of all numbers in the middle row is the same as in the middle column
the sum of the squares of all numbers in the left diagonal is the same as in the right diagonal
the sum of the third powers of all numbers in the middle row is the same as in the middle column
the sum of the third powers of all numbers in the left diagonal is the same as in the right diagonal

Mathematical statement (easy to proof):

If a magic square fulfils the conditions 1 and 3, then it also owns the features 5
If a magic square fulfils the conditions 1 and 4, then it also owns the features 6
If a square is center symmetric, then two rows or two columns symmetrically located to the center have equal squares-sums and equal third-powers-sums

The complete set (96 squares) consist of 16 sets, each containing 6 squares that belong to the same transformation-group. From each of the 16 groups I show only one square.

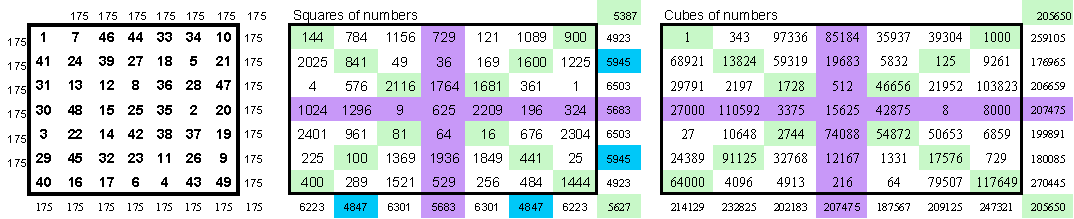
There are 11 magic squares of order 7 with the following features

pandiagonal
center symmetric (associative)
letter H as quadrant magic pattern
the squares of the numbers in the H-patterns have equal sums

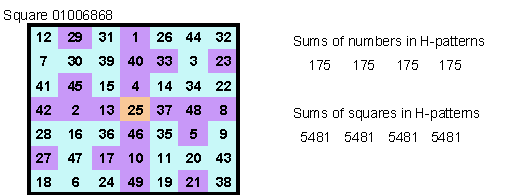There are 20 magic squares of order 7 with the following features

pandiagonal
center symmetric (associative)
letter H as quadrant magic pattern
a magic 3 by 3 array is inlaid (red numbers)
Additional features of square 14
the sum of the squares of all numbers in the middle row is the same as in the middle column
the sum of the cubes of all numbers in the middle row is the same as in the middle column

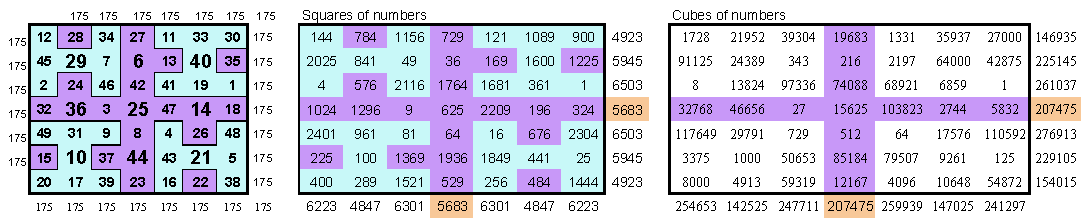
There are 30 magic squares of order 7 with following the features

pandiagonal
center symmetric (associative)
The squares are covered (except for the center cell) symmetrically by 3-cell-tiles

The numbers in each tile sum up to 3x25 = 75

Square 00384300

These 4 types of ultra letter squares are all pandiagonal center symmetric (associated) magic

a. the sum of the 10 numbers in each letter A sum to 250. The squares of these numbers sum to 8362. There are 11 order-7 magic squares with these features.

b. the sum of the 7 numbers in each letter C and H sum to 175. The squares of these numbers sum to 5721. There is only 1 magic square with these features?

Squares c. and d. are shown twice because the patterns overlap.

c. the sum of the 10 numbers in each letter A sum to 250. The squares of these numbers sum to 7622. There are 5 magic squares with these features.

d. the sum of the 10 numbers in each letter A and W sum to 250. There are 60 magic squares with these features.

Walter Trump has a web page on this subject with much more detailed information at http://www.nefkom.net/trump/magic-squares

.Please send me Feedback about my Web site!