Compact Squares

Compact (from my Bibliography)

Gakuho Abe used this term for a magic square where the four cells of all 2x2 squares contained within it summed to 4/m of S.
Note that this is a requirement for Ollerenshaw’s most-perfect magic squares.
[1] Gakuho Abe, Fifty Problems of Magic Squares, Self published 1950. Later republished in Discrete Math, 127, 1994, pp 3-13.

On April 15, 2007 Aale de Winkel emailed a proof stating that any {compact} square is {panmagic} for the sum of corners of even subsquares:

On April 17, Aale sent a clarification

Harvey {compact}ness is a premise (startpoint) of the proof, the proof states in any {compact} square the sum of the four corners of an even subsquare sum to the same sum. I don't think the reverse is provable!.

Putting it more direct you need to test a square for {compact}ness, you then know that it is panmagic for all possible figures you can form using even square corners, which means most (if not al) patterns on your Franklin page. (the statement is thus powerful)

The same day, Walter Trump sent a message confirming Aale’s proof.

Also the same day, Donald Morris sent a message saying that corners of all rectangles (and squares) of a compact magic square summing correctly, as long as both dimensions are an even number, further confirming Aale’s proof.

Slightly digressing.
I have long wondered if all pandiagonal magic squares were compact. I do not remember seeing one that was not.
Walter’s message of April 17, 2007 included this order 8 pandiagonal magic square that was not compact (although 4 outside corners sum to 130)!
i.e. All pandiagonal magic squares are not compact.

4 outside corners of a magic square summing to 4S/m does not imply that the square is compact, or even pandiagonal!
(Corners of all order-4 squares sum to 34!)

Trump pandiagonal, not compact
22 07 31 59 45 32 09 55
14 46 54 26 29 27 48 16
21 63 24 12 13 47 57 23
62 28 01 50 60 04 30 25
40 35 61 05 15 64 37 03
42 08 18 52 53 41 02 44
49 17 38 36 39 11 19 51
10 56 33 20 06 34 58 43

Then still more discussion.
Walter Trump sent an order-8 square constructed by a Mr. Woodruff in 1916.
I uncovered a square with almost similar features sent me by Donald Morris in 2005.
Aale de Winkel reported that the Woodruff square could be converted to a bent-diagonal type square simply by shifting the square 2 rows and columns down to the right.

Woodruff pandiagonal square  Woodruff (modified)          Morris pandiagonal square
01 32 34 63 37 60 06 27      52 45 55 42 24 09 19 14      60 53 04 13 20 29 44 37
48 49 15 18 12 21 43 54      29 04 26 07 57 40 62 35      06 11 62 51 46 35 22 27
19 14 52 45 55 42 24 09      58 39 61 36 30 03 25 08      61 52 05 12 21 28 45 36
62 35 29 04 26 07 57 40      23 10 20 13 51 46 56 41      03 14 59 54 43 38 19 30
25 08 58 39 61 36 30 03      44 53 47 50 16 17 11 22      63 50 07 10 23 26 47 34
56 41 23 10 20 13 51 46      05 28 02 31 33 64 38 59      01 16 57 56 41 40 17 32
11 22 44 53 47 50 16 17      34 63 37 60 06 27 01 32      58 55 02 15 18 31 42 39
38 59 05 28 02 31 33 64      15 18 12 21 43 54 48 49      08 09 64 49 48 33 24 25

Feature Comparison	Woodruff	Morris	Woodruff (modified)
Associated	Yes	No	No
Pandiagonal magic	Yes	Yes	Yes
Compact all 2x2 squares sum to S	Yes	Yes	Yes
Half rows and half columns = S	Yes. Starting on 1^st & 5^th rows & columns	Yes. Starting on 1^st & 5^th rows & columns	Yes. Starting on 3rd & 7^th rows & columns
Complete bent diagonals	No – horizontal only, starting on 3rd & 7^th col.	Yes – starting on 1^st & 5^th rows & columns	Yes – starting on 1^st & 5^th rows & columns
4x4, 6x6, 8x8 circles	Yes	Yes	Yes
Corners of 2x2, 2x4, 2x6, 2x8, 4x4,4x6, 4x8, 6x6, 6x8, 8x8	Yes	Yes	Yes
Aale’s letters A, a, C, c, E, e, F, f	Yes	Yes	Yes
Cross & diamond	No	No	No

Aale’s proof showed that corners of all rectilinear shapes with even dimensions sum to 4/m of S.
Circles of even order sum correctly to xS/m (where x = number of cells in figure and m = order)
All of Aale’s letters that I tested also summed correctly.
In all cases, this includes wrap-around. The corner of the figure may start on any cell in the square!

After checking Aale’s letters, I thought maybe the outside dimensions can be anything, as long as the total number of cells used is a multiple of 4. Of course, as Aale explains, the shape can be considered to be in an array of even dimensions filled with required blank cells.
The array size of the ‘letter’s’ checked were 6x4, 5x4,and 5x3.
After checking the cross (8x5) and diamond (8x7), I realize that this is incorrect.
I leave the reason for this, for someone else to explain .

Available for download is my Compact_8-MS.xls. I used it to check out and compare the above 3 squares, plus an order 8 Franklin pandiagonal magic square by Peter Loly. The Loly square is similar to the above, with the extra feature that correct half rows start on all odd columns.

Addendum (July 12, 2008: Compact_8-MS.xls has been expanded to compare 7 different order-8 magic squares.
One of these is from Dwane Campbell who has a comprehensive new site containing hypercube generators.

Shapes tested in above squares

The letter patterns are some of those suggested by Aale de Winkel in an email of April 20, 2007.

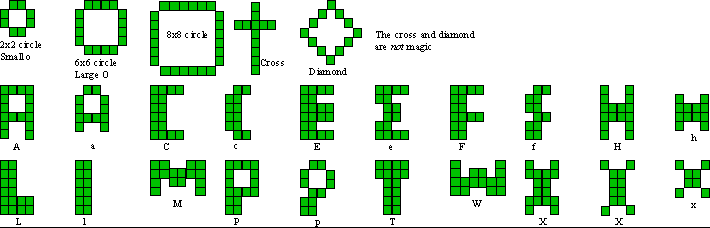
The above shapes are some of the preliminary ones first suggested by Aale.

He has a comprehensive entry on this subject (and more refined shapes) in The Magic Encyclepedia. (Look at Compact under C.)