 |
 |
 |
 |
 |
![]()
In the last several years there has been a marked increase in activity concerning Knight Tours. Much of this is reported on Guenter Stertenbrink’s website. [1]
A knight tour is a series of steps performed by a chess knight on x by y array of cells. If x=8 and y=8 then we have a standard chess board.
If we assign a number to each step, is it possible to complete a knight tour such that these numbers form a magic square? This has been an open question for many years. In August 2003, this question was answered. No, it is not possible to have a magic knight tour of an 8x8 (chess) board. [1][2][3]
In much of the knight tour literature, a tour is called MKT (Magic Knight Tour) if only the rows and columns, but not diagonals, sum correctly. I (and some others) define a MKT as requiring that rows, columns and diagonals must sum correctly. This is the same definitions as used for a Magic Square (MS). This is the definition used when making the above claim that no MKT exists for an 8x8 board.
The attempt to cover all the
squares of a chess board with knight moves, without going over the same square a
second time, is perhaps, as old as the invention of the game itself. In a
Persian paper written before the year 899 appeared these words;
| “Finally, I will show you how to move a knight from any individual square on the board so that it may cover each of the remaining squares in as many moves…” [4] |
Games Ancient and Oriental and How to Play Them,
covers this subject on pages 309 to 356. It starts off with a 17 item
bibliography of material dating between 1750 and 1854! It includes 66 8x8 tour
diagrams with symmetrical features.
Leonard Euler worked on this problem (around 1750?)and developed a general routine where the tour could start on any cell. It was ingenious but sometimes complicated and laborious.
| Here is an example of a
pattern developed as a personal calling card by a Dr. Roget in 1840. This
resulted from his method, much improved from Euler’s.Dr.
Roget’s method considered only one quadrant of the square, then copied the pattern to the other 3 quadrants. Because this pattern is re-entry, you may start this pattern on any of the 64 cells! In this pattern, all columns sum to 260, but no rows or diagonals. |
|
![]()
In much of the knight tour
literature, a tour is called MKT (Magic Knight Tour) if only the rows and
columns sum correctly. I (and some others) define a MKT as requiring rows,
columns and diagonals must sum correctly. This is the same definitions as used
for a Magic Square (MS). This is the definition used when making the above claim
that no MKT exists for an 8x8 board.
If the starting and ending cells are a
knight’s move apart, the tour is called reentrant.
The term SMKT (Semi-Magic
Knight Tour) will be used for a tour where all rows and all columns, but not the
2 main diagonals, sum to the constant. J. C. Meyrignac’s program proved that
there are no MKT’s on an 8x8 board, but there are 140 distinct SMKT’s.
Dan Thomasson has classified and attractively diagrammed these tours.[3]
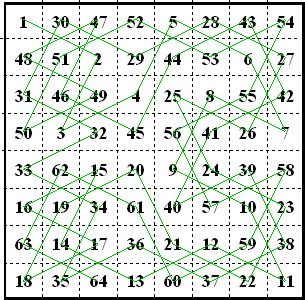 |
The first semi-magic knight tour on a chess board? All rows and columns sum to 260, but diagonals equal 210 and 282 so this is only semi-magic. All 2x2 squares sum to 130. The tour is not normally considered reentrant. However, if you consider wrap-around, as in a pandiagonal magic square, then yes, cell 1 is only one knight move away from cell 64! This tour was constructed by a Mr. William Beverley and published in The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, in 1848. {[4], page 324; [5], pages 191-192.}
|
![]()
|
George Jelliss shows various knight tours on various size boards on his Knight Tour Notes page. [6] to the right is one of four 12x12 magic knight tours (MKT) by Awani Kumar discovered in 2003. The 12 rows, 12 columns and 2 diagonals all sum to 870.
The following three early reentry knight tours on |
|
![]()
|
Awani Kumar has published his investigations into knight tours of magic cubes and cuboids on G. P. Jelliss’s Games and Puzzles Journal. [7] Here is Figure 14 from that Journal On this almost MKT of a 2x4x4 cuboid, all rows and columns sum to 66. However, only 8 (one-half) of the pillars sum to 66/2. All 2x2 horizontal squares also sum to 66. Among many other examples, Kumar shows an order-4 magic knight tour cube (rows, columns, pillars and triagonals) in figure 41. However, I show an earlier one by Guenter Stertenbrink. [8] Kumar reports that a magic knight tour of the order 8 cube has yet to be found. So far, his best effort has one-third of the orthogonal lines summing correctly to 2052. |
||||||||||||||||||||||||||||||||
|
Dan Thomasson illustrates his method of
attempting to make an 8x8x8 magic knight tour. [9]
|
|||||||||||||||||||||||||||||||||
 |
Erich Friedman has a page where he
discusses MKT but shows a large variety of other types of knight and other
chess piece tours. [10] |
||||||||||||||||||||||||||||||||
News Flash!
May 22, 2007.
Awani Kumar announced by email the first two
solutions to an order- 8 Magic Knight Tour. All rows, columns, pillars, and the
4 triagonals
of this cube sum to 2052. This cube is simple magic with no included magic
squares. The knight tour is re-entrant.
Guenter Stertenbrink confirmed (also by email) the same day that all knight moves are correct.
On June 19, 2007 Kumar announced an order-12 magic knight tour cube.
This is the listing of the first of his two order-8 cubes.
A B 19 482 509 16 461 480 35 50 510 15 20 481 472 453 58 43 490 27 8 501 36 49 462 479 7 502 489 28 57 44 471 454 511 14 17 484 465 452 63 46 18 483 512 13 460 473 38 55 6 503 492 25 64 45 466 451 491 26 5 504 37 56 459 474 117 100 411 398 429 448 67 82 414 395 116 101 440 421 90 75 410 399 120 97 68 81 430 447 113 104 415 394 89 76 439 422 387 118 109 412 433 420 95 78 108 413 390 115 428 441 70 87 112 409 386 119 96 77 434 419 391 114 105 416 69 88 427 442
C D 495 30 1 500 33 52 463 478 2 499 496 29 60 41 470 455 22 487 508 9 464 477 34 51 507 10 21 488 469 456 59 42 3 498 493 32 61 48 467 450 494 31 4 497 40 53 458 475 506 11 24 485 468 449 62 47 23 486 505 12 457 476 39 54 99 406 397 124 65 84 431 446 396 125 102 403 92 73 438 423 400 121 98 407 432 445 66 83 103 402 393 128 437 424 91 74 405 388 123 110 93 80 435 418 126 107 404 389 72 85 426 443 122 111 408 385 436 417 94 79 401 392 127 106 425 444 71 86
E F 259 274 237 256 213 318 195 300 282 267 248 229 314 209 304 199 238 255 260 273 292 203 214 317 247 230 281 268 207 296 313 210 287 270 241 228 315 212 301 198 262 279 236 249 216 319 194 297 242 227 288 269 206 293 316 211 235 250 261 280 289 202 215 320 369 136 159 362 165 334 339 188 154 367 376 129 330 161 192 343 158 363 372 133 340 187 326 173 373 132 155 366 191 344 169 322 135 146 361 384 331 164 189 342 368 377 130 151 168 335 338 185 364 381 134 147 190 341 172 323 131 150 365 380 337 186 327 176
G H 239 254 257 276 291 204 309 222 246 231 284 265 208 295 218 305 258 275 240 253 310 221 196 299 283 266 245 232 217 306 303 200 243 226 285 272 205 294 219 308 234 251 264 277 290 201 312 223 286 271 244 225 220 307 302 197 263 278 233 252 311 224 193 298 359 370 137 160 179 348 325 174 144 153 354 375 352 183 170 321 140 157 358 371 166 333 180 347 355 374 141 156 329 162 351 184 145 360 383 138 349 182 171 324 378 143 152 353 178 345 328 175 382 139 148 357 332 163 350 181 149 356 379 142 167 336 177 346
[1] Guenter Stertenbrink, Computing Magic Knight Tours at
http://magictour.free.fr/
[2] Eric Weisstein’s Mathworld has this news item
http://mathworld.wolfram.com/news/2003-08-06/magictours/
[3] Iver Peterson’s Trek Talk also reported this news
http://www.maa.org/mathland/mathtrek_10_06_03.html
[3] Thomasson’s 4x4 tour diagrams are at
http://www.borderschess.org/SMKT2.htm
[4] Edward Falkener, Games Ancient and Oriental and How to Play Them, Dover Publ.
1961, 486-20739-0. This book was first published in 1892
[5] Martin Gardner, Mathematical Magic Show, Knopf, 1977, 0-394-40822-5
[6] George Jellis’s tours of rectangles at
http://www.ktn.freeuk.com
[7] Awani Kumar’s 3-D knight tours are at
http://www.gpj.connectfree.co.uk/gpj43.htm
[8] Stertenbrinks 4x4x4 magic knight tour is shown on my
Unusual Cubes page.
[9] Thomasson’s 8x8x8 attempt is at
http://www.borderschess.org/KTMS.htm
[10] Erich Friedman’s page on chess piece tours
http://www.stetson.edu/~efriedma/mathmagic/0805.html
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
this page originally posted April 14, 2007
This page last updated
August 12, 2008
Copyright © 2002 by Harvey D. Heinz