 |
 |
 |
 |
 |
On this page we will digress a little
and consider 3 and 4 dimensional objects and other types of graphs.
Actually, many of these are not polygons, but can have similar magical
properties to perimeter magic polygons.
I have taken many of thee drawings from [1], and present them with a minimum of
descriptive text.
[1] H. D. Heinz and J. R. Hendricks, Magic Square Lexicon: Illustrated, 2000, , 184pp +
Face magic and anti-magic cubes
Magic
The first eight digits can be placed on the corners (vertices) of a cube in 1680
different ways. It is possible to place them in such a manner that the sum of
the four integers on each of the six faces sum to the same value.
It turns out that the there is only one set of two groups of four that can be
used to construct an order-2 face magic cube. That is 1, 4, 6, 7 and 2, 3, 5, 8.
These two sets can be placed on opposite faces of the cube to produce 6
different order-2, face magic solutions. All have face sums of 18. [2]
Figure A.
is one of the six solutions.
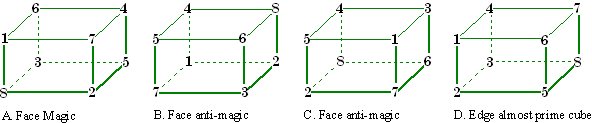
Anti-magic
It is possible to place the digits 1 to 8 on the vertices of a cube in such a
manner that each face sums to a different value. If these sums are in arithmetic
progression, the cube is anti-magic.
Figures B and C are two of the 13 possible solutions. 12 of these consist of 6
complement pairs, one is self-complementing.
There are no edge-magic or anti-magic order-2 cubes. However, the sums of 11 of the 12 edges of Figure D are prime numbers (but with duplication). [3]
Can you find solutions to order-3 face or edge magic cubes?
[2] C. W.
Trigg, , Second Order Perimeter-magic and Perimeter-antimagic Cubes,
Mathematics Magazine, 47(3), 1974, pp.95-97.
[3] C. W. Trigg, Eight Digits on a Cubes Vertices, Journal of
Recreational Mathematics, 7:1, 1974, pp.49-55, .
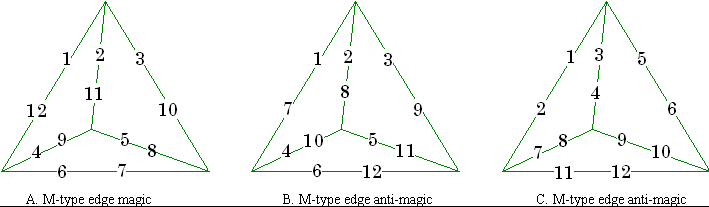
Magic
There are no order-2 (Trigg calls these V-type) edge magic tetrahedrons. [3]
There are no
order-3 edge magic tetrahedrons (using consecutive integers)
Figures A, B, and C illustrate three non-normal solutions. A does not use the integer
4, B. does not use the integers 1 or 11, C. Does not use the integer 2.

Anti-magic
There are no order-2 edge anti-magic tetrahedrons.
There are a total of 376 edge anti-magic tetrahedrons of order 3 (Trigg calls
these VM-type) with edge sums in arithmetic progression. Figure D. is one
solution .
Figure E is a richer solution (1 of 16 of this type). The edge sums are 7, 8, 9,
10, 11, 12, and the vertex only sums (i.e. order-2) are 3, 4, 5, 6; giving ten
consecutive sums!
![]()
M-type Edge Magic Tetrahedrons
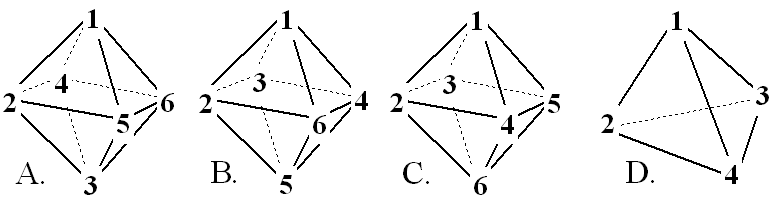
Magic
If one digit is placed at each edge midpoint (none at the vertices), the polygon
is trivially edge anti-magic.
The first12 integers may be placed in pairs near the midpoints of the edges (of
the tetrahedron), so that all edges sum the same. Figure A
Anti-magic
There are a large number of edge anti-magic tetrahedrons of this type. B and C
show two of them.
[4] C. W. Trigg, Edge-Magic and Edge-Antimagic Tetrahedrons, Journal of Recreational Mathematics, 4:4, 1971, pp.253-259, .
Perimeter Face Anti-magic Octahedrons
As all the faces of a polyhedron are triangles, it is impossible to place distinct integers on its vertices so that every triangle will have the same perimeter sum. Therefore, no such polyhedron can be magic. However, if the perimeter sums are all different the polyhedron will be perimeter anti-magic.
In the case of an octahedron it turns out that there are 15 basic ways to distribute the digits 1 to 6 on the vertices with eight different perimeter sums. Of these 15, five produce distinct perimeter sums for the eight triangles and so are perimeter anti-magic.
Figures A. and B. may each be complemented by subtracting each number from 7, to provide another solution. C. is self-complementing.
[5] C. W. Trigg, Perimeter Anti-magic tetrahedrons and Octahedrons, Journal of Recreational Mathematics, 11:2, 1978-79, pp.105-107.
D. shows the basic way to arrange the integers 1 to 4 on the vertices of a tetrahedron. The perimeter sums are in the arithmetic progression order 6, 7, 8, 9, making this a true, face anti-magic tetrahedron. The edge sums of D are almost unique, meaning this is also an almost edge anti-magic tetrahedron!
These figures are order-2 (2 integers per edge). Investigations into order-3 (and higher) figures of this type are still required.
![]()
Mapping and Perimeter Magic
Mapping is a transformation of one image into another one.
In A., the cube is face perimeter magic with the vertices mapping to the triangles of the star. The octahedron is vertex magic with the edges of the eight triangles mapping to the star triangles.
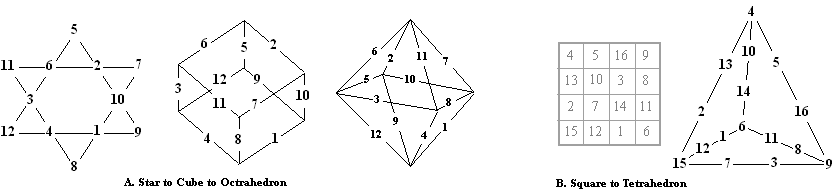
In B. the order-4 magic square is mapped to an order 2 perimeter magic tetrahedron.
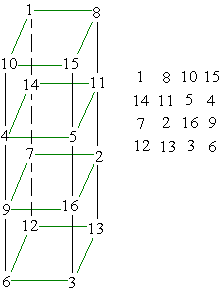
Face Magic Stacked Parallelograms
|
The corner numbers of these 16 parallelograms all sum to 34 (ie face magic), as do the 4 numbers in each of the four vertical lines. They were mapped from the order 4 pantriagonal magic square shown. More on Perimeter magic cubes is on my Unusual magic cubes page. [6]
[6] My previously written page on perimeter magic cubes; http://members.shaw.ca/hdhcubes/cube_unusual.htm#Perimeter-magic |
 |
![]()
Magic Dodecahedron
|
Shown here is a Schlegel diagram (graph) of the platonic solid 12 faced dodecahedron. The numbers 1 to 25 are placed at the vertices of the faces in such a way that all 12 faces are magic. The diagram is placed inside a circle and 5 radial lines have been added. These lines and the circle also sum to the constant. This diagram was taken from a book published in Russia in 1964. [7]
[7] A. P. Domoryad, Mathematical Games and Pastimes, Russia, 1964, page 103. |
|
![]()
Tree-planting Graphs
|
Your aid I want, nine trees to plant In rows just half a score; And let there be in each row three. Solve this: I ask no more. In 1821, John Jackson published this ditty in Rational Amusements for Winter Evenings. Figure A. is the answer to Jackson’s little poem. |
 |
Tree-planting graphs are so-called because
they result from the effort to arrange as many “trees” as possible in a minimum
number of lines, each containing the same number of “trees”. This problem was
made popular by H. E, Dudeney (but introduced by John Jackson 75 years earlier).
See [8] for a good introduction to this type of problem, although you will
find it mentioned in many books on recreational mathematics.
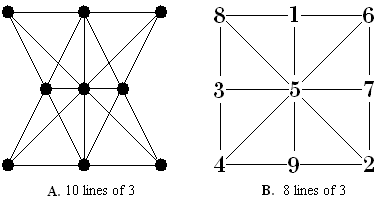
In keeping to the theme of magic perimeters and graphs, I like to replace the ‘trees” with consecutive integers in such a way that the lines are magic. Figure B. is the order 3 magic square with 8 lines of 3 numbers all adding to the same constant.
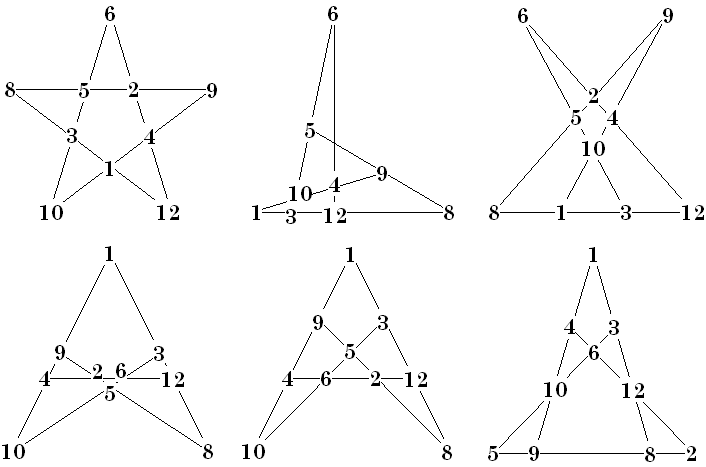
The figure below illustrates an
order-5 magic star I have mapped to 5 other isomorphic “tree-planting”
graphs. [1]
These 6 graphs all have 10 numbers that appear in 5 lines of 4 numbers. Notice
however, that unlike most examples I have shown, these 10 numbers are not
consecutive. It is impossible to place the numbers 1 to 10 on a 5-pointed star
so that all lines sum the same.
[1] H.
D. Heinz and J. R. Hendricks, Magic Square Lexicon: Illustrated, 2000, ,
184pp +
[8]
Mathematical Recreations, Edited by David A. Klarner, Dover Publ., 1998,
0-486-40089-1, Planting Trees, by Stefan Burr, pp90-99.
Super and Anti-magic Graphs
Graph – super-magic
A graph with q edges is said to be super-magic if it is possible to label the edges with the numbers 1, 2, 3, …, q in such a way that at each vertex v the sum of the labels on the edges incident with v is the same.
Many super-magic graphs are isomorphic to magic squares, as the following examples illustrate. Solid vertices in these graphs represent the rows of the magic square., hollow vertices the columns. These graphs is bipartite because no two like vertices are directly connected by an edge.

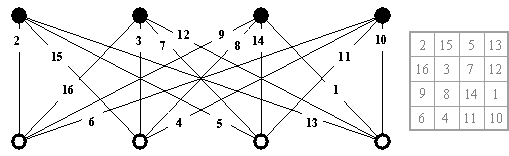
Graph - Anti-magic
A graph with q edges is said to be anti-magic if it is possible to label the edges with the numbers 1, 2, 3, …, q in such a way that at each vertex v the sum of the labels on the edges incident with v is different.
Many anti-magic graphs are isomorphic to magic squares, as the following example illustrates. This graph is isomorphic to the order-4 anti-magic square shown in Anti-magic squares. Solid vertices in this graph represent the rows of the magic square., hollow vertices the columns.
Note that unlike anti-magic squares, it is not required that anti-magic graphs have the sums form a consecutive series. In fact, for normal anti-magic squares, at least 1 of the two diagonals must sum to a value in the middle of the series. In the case of this graph, the sums form a series from 30 to 38 but with 34 missing.
[9] Hartsfield & Ringel, Supermagic and Antimagic Graphs, Journal of Recreational Mathematics, 21:2, 1989, pp107-115
Two Different Magic Triangles
|
In an absolute difference
triangle, the number at the apex of a triangle is the difference between
the two numbers on the base of that triangle.
[10] C. W. Trigg, Absolute Difference Triangles, Journal of Recreational Mathematics, 9:4, 1977, pp.271-275. |
|
![]()
| Fractal Triangles Figure A. shows nested triangles with a single digit at the apex of each triangle. If you consider the digit at each end of a line (ie. adjacent vertices) forming two 2 digit numbers, one of these two numbers will always be divisible by seven (in these examples). This example is called a cycle 1 because it oscillates between identical triangles. Figure B. is an example of a cycle 4 Fractal Triangle because, starting from the center there are four different triangles before the center triangle repeats as the outer triangle. The author conjectures that no longer cycles are possible. [11] C. Pickover, C. Ashbacher, Problem 2025, Fractal Triangles, Journal of Recreational Mathematics, 26:1, 1994, pp.69-70. |
|
![]()
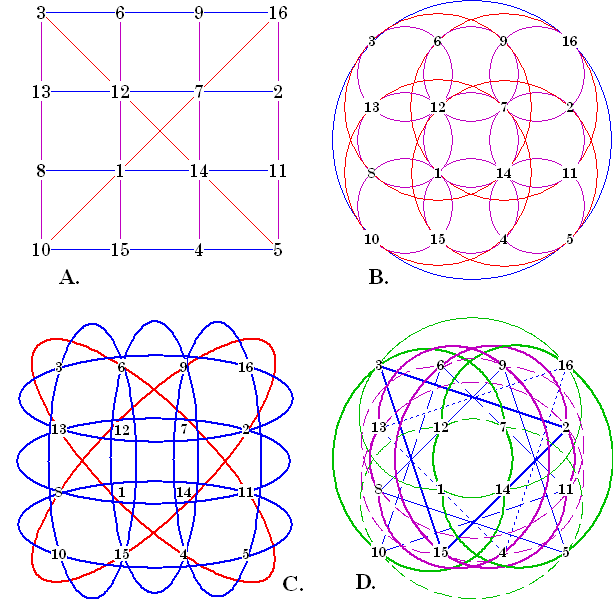
Another magic object related to magic squares, graphs, etc. is the magic circle. Benjamin Franklin, when talking about his famous magic squares, mentioned a magic circle derived from one. See a recreation of this on my Franklin Magic Squares page. [12] link
Here I show a set of magic circles, all related to the same order-4 pandiagonal magic square. It is number 469 in the sorted list of all 880 order-4 basic magic squares. All 48 pandiagonal magic squares of this order contain all the patterns shown in this set of four graphs. This is not necessarily true for other orders of pandiagonal magic squares.
A., in the figure, is the magic square I use for this example. Shown are the basic requirements for all magic squares (ie all rows, columns, and the two main diagonals must sum to a constant. To be classed as pandiagonal, two other patterns are required. These appear in parts C. and D.
B. Contains 9 small circles, each of which connect to 4 numbers that sum to the constant 34. Also, shown in B. are 4 medium sized circles and one large circle, all of which also connect to 4 numbers summing to 34.
C. contains 2 diagonal ovals which show a pattern required to make the square pandiagonal. C. also shows 3 vertical and 3 horizontal ovals illustrating another magic pattern
D. shows 8 sets of four numbers connected by distorted ovals. All of these sets also sum to 34. Also shown are 4 sets of four numbers connected by triangles. This is the other pattern that is a requirement of pandiagonal magic squares.
| This set of 4 graphs illustrate a total
of 9 patterns (2+3+2+2) that appear in an order-4 pandiagonal magic square.
All combinations of 4 numbers sum to the constant 34.
However, there is one additional pattern in the magic square that is not shown in diagrams B, C or D. Can you find it?
|
 |
![]()
 The six numbers on each of the four circles sum to 39. |
 Each spoke (including the hub) and each rim section sum to 38.
|
 The middle number on each line is the difference between the two outside numbers. |
See a pandiagonal magic square generator using a magic torus on my Unusual Squares page.
[12] An elaborate magic circle appears on my Franklin page.
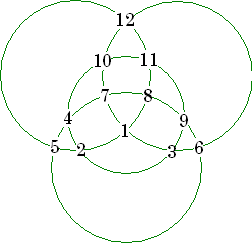
More Magic Graphs
Graphs A and B are self-explanatory. In the “3-D” graph at C, the sum of the 5 lines at each node is 65.
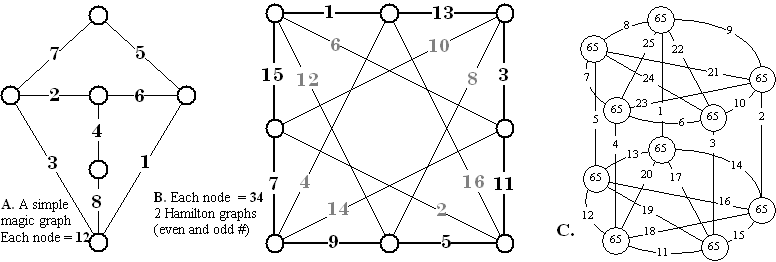
A and B from [9], C is from [1]
![]()
|
10 nodes |
|
| Priming the cube The corners of this cube are labeled with the consecutive integers from 0 to 7 in such a way that two adjacent corners (vertices) always sum to a prime number.
[13] See another prime number graph containing numbers 1 to 22 on my Prime Numbers page. |
"Magic Hexagons" and "12 Magic Circles-6 Magic Squares" are on my More Squares page.
|
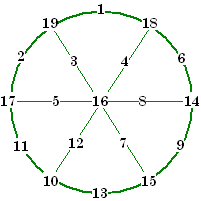
Graceful Graphs In 1972, Solomon Golomb proposed a new type of graph numbering called Graceful Graphs. [14] In it, the nodes are numbered in such a way that the edges connecting them form a set of consecutive numbers starting with 1. The lowest node number is zero, and by necessity, the node numbers are not consecutive. For a graft to be graceful, the highest node number, the highest edge number, and the number of edges must all be equal. Figure A (below) is a tetrahedron and figure C is a Schlegel representation of a cube. Notice in figure B, one line seems to be missing. If that line is added, the diagram becomes one of only 3 ungraceful graphs with fewer then 6 nodes! These graceful graphs are all from Martin Gardner's Mathematical Games column in Scientific American Magazine . [14] [15] |
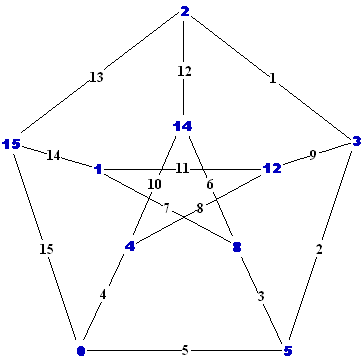 |
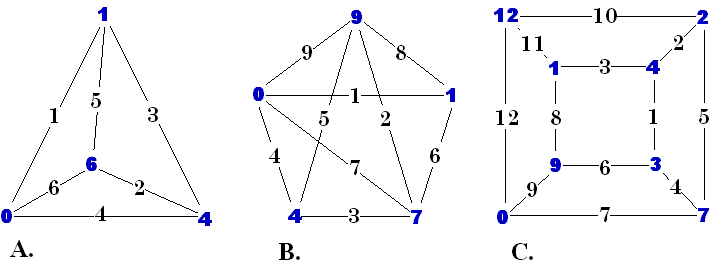
[14] Martin
Gardner, Mathematical Games, Scientific American Magazine, March,1972, pp
108-112.
[15]
Martin Gardner, Wheels, Life, and Other Mathematical Amusements, W. H.
Freeman, 1983, 0-7167-1589-9, pp 152-165, Golomb’s Graceful Graphs
![]()
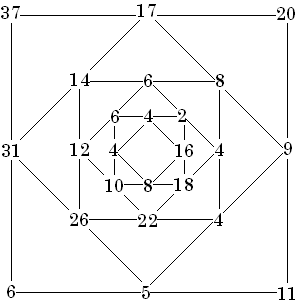
Some graph problems
Tree Problems
These are my patterns. Can you assign consecutive numbers to them so that each
line equals the same value?
A star pattern with 16 numbers in 15 rows of 4 appears on my
Magic Star Updates page.
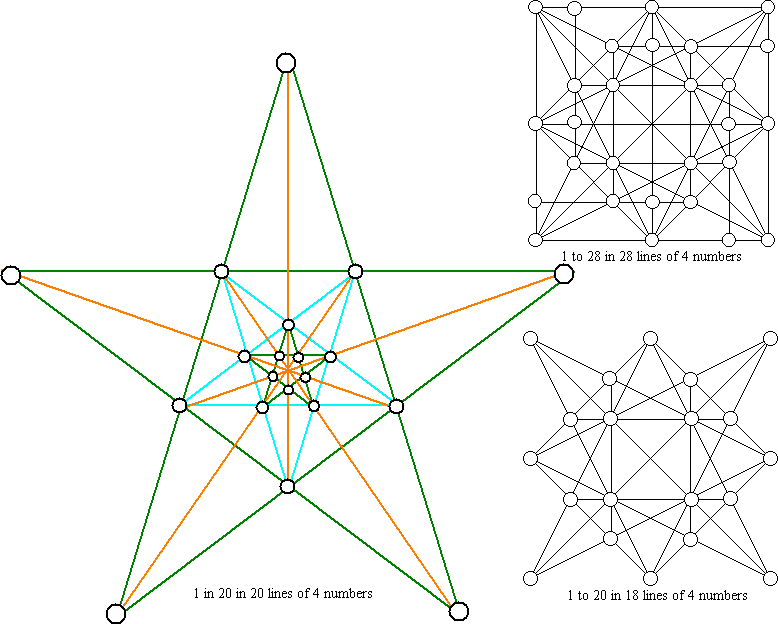
![]()
Graceful graph problems
These three graphs are taken from Gardner's column [14] [15] and presented here
as problems. His column provides the solutions.
Figure A will use edge numbers 1 to 9 and B will use 1 to 22. C will use numbers
1 to 25 for the edges and 0 to 25 for the nodes.
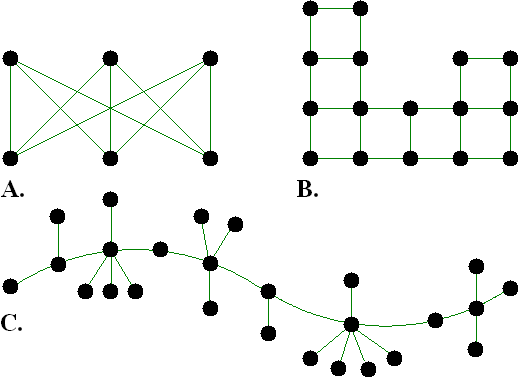
![]()
References
[1] H. D. Heinz
and J. R. Hendricks, Magic Square Lexicon: Illustrated, 2000, , 184pp +
[2] C. W.
Trigg, , Second Order Perimeter-magic and Perimeter-antimagic Cubes,
Mathematics Magazine, 47(3), 1974, pp.95-97.
[3] C. W. Trigg, Eight Digits on a Cubes Vertices, Journal of
Recreational Mathematics, 7:1, 1974, pp.49-55
[4] C. W. Trigg,
Edge-Magic and Edge-Antimagic
Tetrahedrons, Journal of Recreational
Mathematics, 4:4, 1971, pp.253-259.
[5]
C. W. Trigg, Perimeter Anti-magic tetrahedrons and Octahedrons, Journal
of Recreational Mathematics, 11:2, 1978-79, pp.105-107.
[6] My
previously written page on perimeter magic cubes;
http://members.shaw.ca/hdhcubes/cube_unusual.htm#Perimeter-magic
[7] A. P. Domoryad, Mathematical Games and Pastimes, Russia, 1964,
page 103.
[8]
Mathematical Recreations, Edited by David A. Klarner, Dover Publ., 1998,
0-486-40089-1, Planting Trees, by Stefan Burr, pp90-99.
[9]
Hartsfield & Ringel, Supermagic and
Antimagic Graphs, Journal of Recreational
Mathematics, 21:2, 1989,
pp107-115
[10] C. W. Trigg, Absolute Difference Triangles, Journal of
Recreational Mathematics, 9:4, 1977, pp.271-275.
[11] C. Pickover, C. Ashbacher,
Problem 2025, Fractal Triangles, Journal of Recreational Mathematics, 26:1,
1994, pp.69-70.
[12] An elaborate magic circle appears on my
Franklin page at at
http://www.geocities.com/~harveyh/franklin.htm#circle.
[13] See another prime number graph
containing numbers 1 to 22 on my Prime Numbers page at
http://www.geocities.com/~harveyh/primes.htm#Pairs equal Prime.
[14] Martin Gardner,
Mathematical Games, Scientific American Magazine, March,1972, pp 108-112.
[15]
Martin Gardner, Wheels, Life, and Other Mathematical Amusements, W. H.
Freeman, 1983, 0-7167-1589-9, pp 152-165, Golomb’s Graceful Graphs
![]()
. Please send me Feedback
about my Web site!
Please send me Feedback
about my Web site!![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
Last updated October 17, 2008
Copyright © 1999 by Harvey D. Heinz