 |
 |
 |
 |
 |
On this page I will present some condensed information on perimeter magic polygons of sides 4, 5, 6, etc. I will also present a brief description on a simple construction method.
| Perimeter Magic Squares | Perimeter Magic Pentagons |
| Perimeter Magic Hexagons | Constructing Odd Order PMPs |
This table shows relevant information for 4 sided PMPs.
|
Squares |
Order 3 |
Order 4 |
Order 5 |
Order 6 |
Order 7 |
Order 8 |
|
Minimum S |
12 |
22 |
37 |
55 |
78 |
104 |
|
Maximum S |
15 |
30 |
48 |
71 |
97 |
128 |
|
Integers used |
8 |
12 |
16 |
20 |
24 |
28 |
|
Minimum Vertex sum |
12 |
10 |
12 |
10 |
12 |
10 |
|
Maximum Vertex sum |
24 |
42 |
56 |
74 |
88 |
106 |
|
Number of basic solutions |
6 |
146? |
|
|
|
|
* These table are calculated using the formulae in [1] and [2]
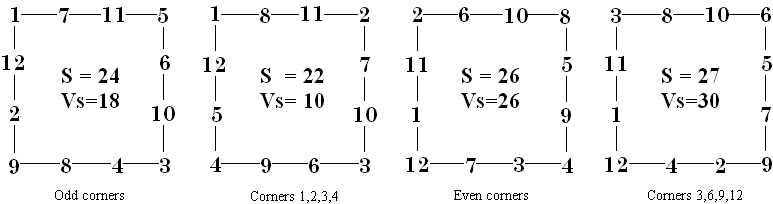
These are the six possible solutions for order 3. They are in sorted order with 1 and 6, 2 and 5, 3 and 4 the complement pairs.
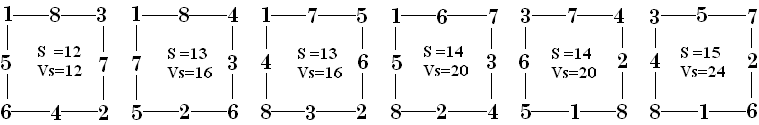
Order 4 has a total of 146 basic solutions (I think). Here are four.
Some examples for higher orders of perimeter magic squares.
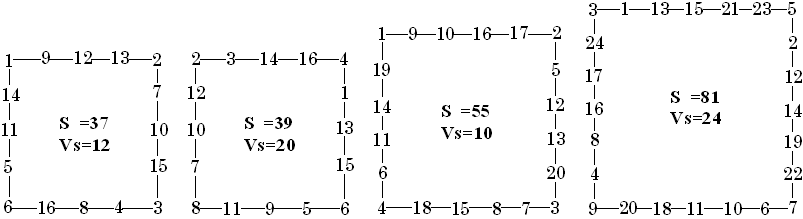
For information on Perimeter magic cubes see my http://members.shaw.ca/hdhcubes/cube_unusual.htm#Perimeter-magic
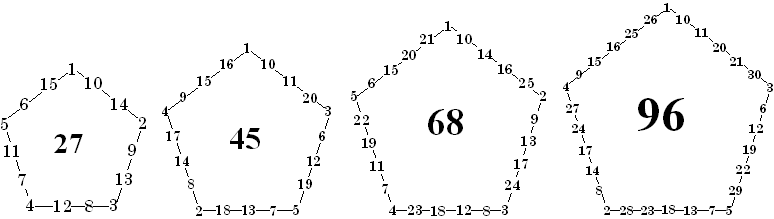
These are the only order-3 perimeter magic pentagons (not
counting the 4 rotations and 5 reflections of each).
By computer search, I have found 6074 solutions for order-4. However, I have not
confirmed that that is all the possible basic solutions.

These six solutions are shown arranged in complement pairs,
![]()
This table shows relevant information for 5 sided PMPs.
|
Pentagons |
Order 3 |
Order 4 |
Order 5 |
Order 6 |
Order 7 |
Order 8 |
|
Minimum S |
14 |
27 |
45 |
68 |
96 |
129 |
|
Maximum S |
19 |
37 |
60 |
88 |
121 |
159 |
|
Integers used |
10 |
15 |
20 |
25 |
30 |
35 |
|
Minimum Vertex sum |
15 |
15 |
15 |
15 |
15 |
15 |
|
Maximum Vertex sum |
40 |
65 |
90 |
115 |
140 |
165 |
|
Number of basic solutions |
6 |
6074? |
|
|
|
|
![]()
The following four perimeter magic pentagrams were constructed with the help of a simple routine (once the smallest odd and even orders are designed. Divide the extra numbers required into pairs with equal sums. Then add one of these pairs to each side of the original PMP to get the next larger order of the same parity.
In this case, to obtain the order 6 PM pentagon, partition the extra numbers (16 to 25) into 5 pairs each totalling 41. Then add one of these pairs of numbers to any side of the originating order 4.
![]()
| A Perimeter Bi-magic order-4 pentagon On the previous page we saw a Perimeter Bi-magic order-4 triangle. Can someone find an Perimeter Bi-magicorder-4 square or hexagon? |
|
This table shows relevant information for 6 sided PMPs.
|
Hexagons |
Order 3 |
Order 4 |
Order 5 |
Order 6 |
Order 7 |
Order 8 |
|
Minimum S |
17 |
32 |
54 |
81 |
115 |
154 |
|
Maximum S |
22 |
44 |
71 |
105 |
144 |
190 |
|
Integers used |
12 |
18 |
24 |
30 |
36 |
42 |
|
Minimum Vertex sum |
24 |
21 |
24 |
21 |
24 |
21 |
|
Maximum Vertex sum |
54 |
93 |
126 |
165 |
198 |
237 |
|
Number of basic solutions |
20 |
|
|
|
|
|
The 20 basic solutions for order 3 Hexagons
# A B C D E F S Comp. # 1 1 11 5 10 2 12 3 8 6 4 7 9 17 19 2 1 11 5 9 3 12 2 8 7 4 6 10 17 20 3 1 11 5 8 4 10 3 12 2 6 9 7 17 18 4 1 12 6 2 11 5 3 9 7 4 8 10 19 14 5 1 11 7 9 3 4 12 2 5 6 8 10 19 7 6 1 9 8 6 4 12 2 11 5 3 10 7 18 17 7 1 11 8 7 5 3 12 2 6 4 10 9 20 5 8 1 10 8 4 7 9 3 11 5 2 12 6 19 10 9 1 10 8 2 9 6 4 12 3 5 11 7 19 15 10 1 11 8 2 10 4 6 9 5 3 12 7 20 8 11 2 12 6 4 10 1 9 3 8 5 7 11 20 16 12 2 12 6 3 11 5 4 7 9 1 10 8 20 13 13 2 10 7 1 11 5 3 12 4 6 9 8 19 12 14 2 11 7 1 12 3 5 9 6 4 10 8 20 4 15 2 8 10 1 9 7 4 11 5 3 12 6 20 9 16 3 12 4 10 5 8 6 2 11 1 7 9 19 11 17 3 10 8 2 11 1 9 7 5 4 12 6 21 6 18 4 7 11 1 10 3 9 5 8 2 12 6 22 3 19 6 9 7 5 10 1 11 3 8 2 12 4 22 1 20 6 9 7 3 12 2 8 4 10 1 11 5 22 2
Three examples
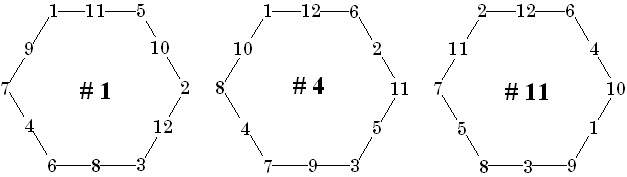
![]()
Three order 4 perimeter magic hexagons with consecutive vertex numbers. All solutions for order-4 PM Hexagons have not yet been compiled (to my knowledge), so we cannot assign solution numbers to these figures.
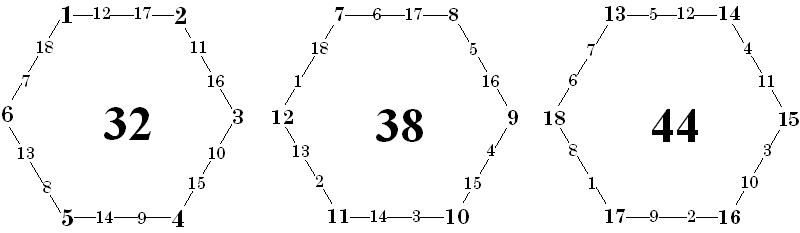
![]()
|
This illustration combines 4 orders of perimeter magic hexagons consisting of consecutive numbers. It is an example of the fact that like magic squares and cubes, these figures also remain magic when a constant is added to each number in the series. In this case, the resulting series
are 1 to 12,
|
|
![]()
| Constructing Odd
Order PMPs
A simple procedure for constructing order 3 perimeter magic polygons is illustrated here. The numbers may be written down in consecutive order as per the sequences shown in the 7-sided and 9-sided polygons here. Then for higher odd orders, these can be modified by adding pairs of numbers to each side (as per discussion under Pentagons). |
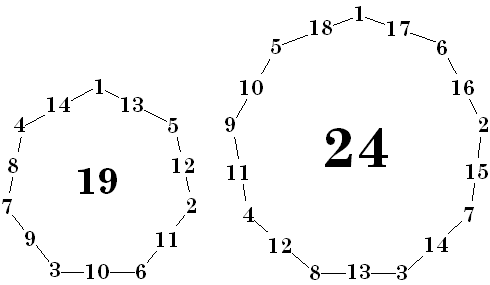 |
![]()
[1] Terrel Trotter, Jr., Normal
Magic Triangles of Order n, Journal of Recreational Mathematics, Vol. 5,,
No. 1, 1972, pp.28-32
[2] Terrel Trotter, Jr., Perimeter-magic Polygons, Journal of
Recreational Mathematics, Vol. 7,, No. 1, 1974, pp.14-20
[3] For information on Perimeter magic cubes see my
http://members.shaw.ca/hdhcubes/cube_unusual.htm#Perimeter-magic
. Please send me Feedback
about my Web site!
Please send me Feedback
about my Web site!![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
Last updated October 19, 2006
Copyright © 1999 by Harvey D. Heinz