 |
 |
 |
 |
 |
In 1972, Terrel Trotter, Jr., then a math teacher in Urbana Illinois, published an article called Normal Magic Triangles of Order n [1]. In 1974, he published a follow up article called Perimeter-magic Polygons [2]. In it he introduced the term Perimeter-magic Polygon, and generalized it to include other polygonal shapes. Since that time, other writers have expanded on the same theme.
On this page, I will attempt to expand on, and summarize the published material on perimeter-magic polygons (PMPs for short) and to add interest, I will include some problems dealing with the subject matter. Because of the nature of perimeter-magic polygons, these problems will be suitable for middle school students. A companion page will feature magic graphs. That page also will include problems. However, these will tend to be much more complicated and will, in many cases, require the use of a personal computer.
Order 3 Perimeter Magic Triangles |
Some Math |
Order 4 Perimeter Magic Triangles |
Larger Perimeter Magic Triangles |
Other Types of PM Triangles |
References |
Additional pages on this subject
PMPs with sides >3 |
Magic 3-D polygons and Graphs |
Perimeter Magic cubes (a previously written page) |
Order 3 Perimeter Magic Triangles
Order-3 is the simplest perimeter- magic triangle, except for order 1 which is trivial (there are no order 2 perimeter-magic objects). Unlike magic squares, cubes, etc., there are multiple magic constants for the same order.
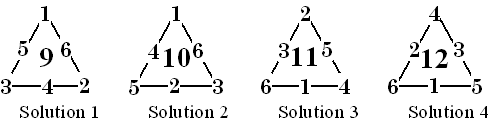 |
Here I show the only PMPs of order 3.
Solution 4 is the compliment of solution 1, and solution
3 is the complement of solution 2 |
Complements.
For any given solution, there is always a complement solution. It is obtained by
subtracting each number in turn from the sum of the first and last numbers in
the series. So if your solution uses the numbers from 1 to 9, another solution
is obtained by subtracting each number from 10 (ie. The sum of the first and
last numbers in the series). This feature applies to magic squares, cubes etc.
as well.
The new solution obtained in this way must then be normalized by rotation and/or reflection, to comply with the above
For higher orders, with many solutions, it is necessary to only find solutions for the smallest half of the possible sums. The higher magic sums may then be obtained simply by complementing these lower solutions.
Rotations and Reflections
|
|
Rotations and Reflections are not
considered unique solutions. Each basic solution has two rotations and each of
these has one (horizontal) reflection, for a total of 6 apparently different
solutions. For other polygons, these numbers would obviously vary. While any one of these six could be considered the basic solution, I have chosen to use the convention described in the next section. |
Standard for Normalized solutions
There are many ways to sort magic
perimeter solutions.
Other writers have chosen to sort by side or vertex totals (or possibly no sort
at all).
For polygons with few solutions, this step is not important. However, as the
number of solutions increases, a sorted list is necessary in order to prevent
possible duplications.
I have chosen to use the following
system.
To facilitate putting polygon solutions in order:
Place the lowest vertex number at the top
Then move clockwise around the polygon and
Enter vertex numbers in order, then
Enter side numbers in order
Arrange list of solutions in sorted order
Order 3 solutions in list order:
In the sorted list below, S=Side sum (i.e. the magic constant, V=Vertex sum, C=the complement solution #, Bold columns are vertices
# A B C S V C
1. 1 6 2 4 3 5 9 6 4
2. 1 6 3 2 5 4 10 9 3
3. 2 5 4 1 6 3 11 12 2
4. 4 3 5 1 6 2 12 15 1
Note that solutions 3 and 4 have been
normalized before being added to the list
An example of complementing and normalizing:
# A B C S V C
1. 1 6 2 4 3 5 9 6 4 Solution 1
4. 6 1 5 3 4 2 Subtract above number from 7
4. 4 3 5 1 6 2 12 15 1 Normalized solution 4
![]()
Formulas required for solving
perimeter-magic polygons.
Trotter covered the mathematic involved in great
detail. Here I am only summarizing.
We are assuming the numbers used are
consecutive starting with 1.
The following notation will be used.
k = the number of
sides of the polygon
n = the number of
integers per side (the order)
S = the magic constant (Trotter used C, but S is consistent with magic square
terminology)
N = the number of
consecutive integers being used
Vertex sum = k[S-1/2(n-1){(n-1)k+1}]
The smallest vertex sum is 1 + 2 + 3
i.e. the 3 smallest integers in the series from 1 to N.
The largest vertex sum is 3n – 3 (that is, the 3 largest integers).
However, because of parity, the 3 smallest integers and the 3 largest integers
may not always give the possible smallest and largest vertex sums. There are two
separate cases, depending on the values of n and k:
If n is even or n and k
are both odd, then
min Vs = ½k(k +
1) max Vs = ½k[(2n – 3)k
+ 1]
When n is odd and k is even, then
min Vs = ½k(k +
2) max Vs = ½(2n-3)k2
The final values we need to determine
are the minimum and maximum values of the magic constant S.
Here again we must have two formulas, depending on the values of n and
k.
If n is even or n and k
are both odd, then
min S = (½n2 – n + 1)k + ½ n)
max S = (½n2 – 1)k + ½ n
When n is odd and k is even, then
min S = (½n2 – n + 1)k + ½ (n
+ 1) max S = (½n2 – 1)k + ½ (n –
1)
A word of caution. These formulas indicate where solutions may be found. On very rare occasions, there may be no solution for a particular value of S. However, only two such cases are known. They are; for a 4th order triangle with S = 18 or 22, and, 3rd order pentagon with S = 15 or 18.
For perimeter magic triangles, a simple
equation gives the number of magic sums for any given order.
Number of different sums = 3n-5. This even allows for the special ‘case
of the two missing sums in the order 4 triangle
Can you find any other cases with no
solution for a value of S between the theoretical minimum and maximum limits?
If there are any such cases, they will always be
an even number because of the complement feature mentioned above.
A table generated from the above formulae has been placed at the beginning of each polygon section following.
(1) Terrel
Trotter, Jr., Normal Magic Triangles of Order n, Journal of Recreational
Mathematics, Vol. 5,, No. 1, 1972, pp.28-32
(2) Terrel
Trotter, Jr., Perimeter-magic Polygons, Journal of Recreational
Mathematics, Vol. 7,, No. 1, 1974, pp.14-20
![]()
I find the simplest method for constructing PMP’s manually is the following:
k = the number of
sides of the polygon
n = the number of
integers per side (the order)
Vs = the sum of the vertex numbers
Ns = sum of the series of numbers used
Ms = the average mid-side sum (ie sum of integers between the two vertices of
each side.
Order 4 Perimeter Magic Triangles
There are 18 basic solutions for order 4
PM Triangles. Note that there are no solutions with magic sums of 18 and 22.
The number of solutions for each sum should be symmetrical.
Sum 17 19 20 21 23 # of solutions 2 4 6 4 2 = 18
The list below contains all solutions for order 4 PM Triangles.
S=Side sum (i.e. the magic constant,
V=Vertex sum, C=the complement solution #,
CS=the complement side sum, CV=the complement vertex sum. Columns A, B, and C are
the vertices
# A B C S V C 1. 1 5 9 2 4 8 3 6 7 17 6 17 2. 1 5 9 4 2 6 7 3 8 19 12 12 3. 1 6 8 2 5 7 3 4 9 17 6 18 4. 1 6 8 4 3 5 7 2 9 19 12 14 5. 1 6 8 5 2 4 9 7 3 20 15 6 6. 2 4 9 5 1 6 8 3 7 20 15 5 7. 2 5 9 3 1 8 7 4 6 19 12 10 8. 2 6 7 5 3 4 8 1 9 20 15 8 9. 2 6 8 3 4 5 7 1 9 19 12 13 10. 3 2 9 7 1 5 8 4 6 21 18 7 11. 3 4 8 5 2 6 7 1 9 20 15 11 12. 3 4 8 6 1 5 9 2 7 21 18 2 13. 3 5 6 7 2 4 8 1 9 21 18 9 14. 3 5 7 6 2 4 9 1 8 21 18 4 15. 4 2 9 5 1 8 6 3 7 20 15 15 16. 4 3 8 5 2 7 6 1 9 20 15 16 17. 7 2 6 8 1 5 9 3 4 23 24 1 18. 7 3 5 8 2 4 9 1 6 23 24 3Some example diagrams:
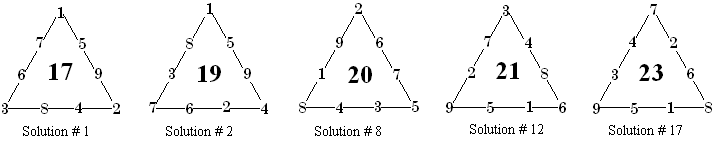
Solution # 17 is the normalized
complement of solution #1, and # 12 is the normalized complement of #2.
Number 8 is it’s own complement.
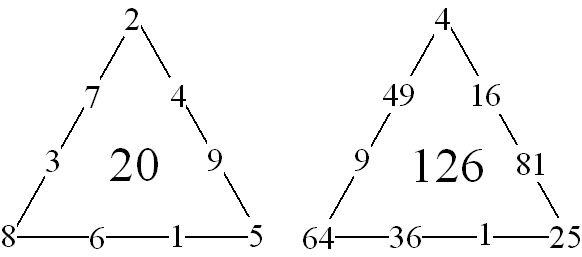 |
Solution number 6 is of special interest because it is bimagic. It was originally discovered by David Collison of California, USA [3]. When each number is squared, the triangle is still perimeter magic. This time with a sum of 126. This suggest another investigation…to find bimagic solutions in other orders (or even trimagic solutions?). |
[3] John R. Hendricks, The Magic Square Course, 2nd edition, 1992, 522 pages +,
![]()
Larger Perimeter Magic Triangles
Order 5 PM Traingles have ten values for S. They range from 28 to 37. Trotter [1] reports that there are 1356 basic (he calls them primitive) solutions.
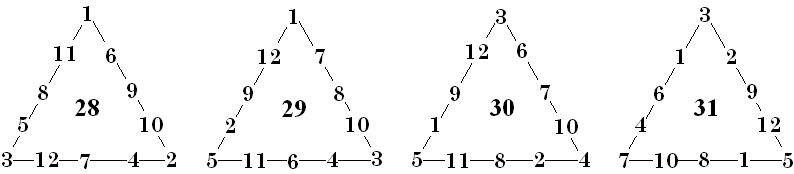
Here I show solutions for the 4 lowest
possible magic sums. By complementing these, you can obtain another solutions
for the 4 highest sums. I leave it to you to find solutions for sums of 32 and
33.
Note that I have not supplied solution numbers to these. The only way that can
be done is to find and list in order all of the possible basic solutions.
![]()
Orders-6 to 8 Triangles
Here is summary information on orders 6 to 8 perimeter magic triangles. For completeness, I included the same information for the smaller triangles.
|
|
Order 3 |
Order 4 |
Order 5 |
Order 6 |
Order 7 |
Order 8 |
|
Minimum S |
9 |
17 |
28 |
42 |
59 |
79 |
|
Maximum S |
12 |
23 * |
37 |
64 |
74 |
97 |
|
Integers used |
1 to 6 |
1 to 9 |
1 to 12 |
1 to 15 |
1 to 18 |
1 to 21 |
|
Minimum Vertex sum |
6 |
6 |
6 |
6 |
6 |
6 |
|
Maximum Vertex sum |
15 |
24 |
33 |
42 |
51 |
60 |
|
Number of basic solutions |
4 |
18 |
1356? |
? |
? |
? |
* For order 4, there are no solutions with sums of 18 or 22.
Following are sample solutions of orders 6, 7, and 8 PM Triangles. The reader is left with a challenge to find additional solutions. Or even, all the solutions for a given order.
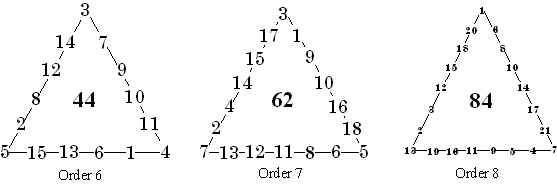
Perimeter magic triagonals are neither as complex, or mathematically challenging as magic squares or cubes. Nevertheless, they can be of interest to anyone who is intrigued with the vast variety of number patterns.
Sunday Ajose [4] proposed a type of triangle where the smallest number on each side is subtracted from the sum of the two largest numbers. For orders greater then 3, the sum of the smaller numbers is subtracted from the sum of the larger numbers on each side. In all cases, to be magic the differences must be the same. He calls this constant d. Some examples follow.
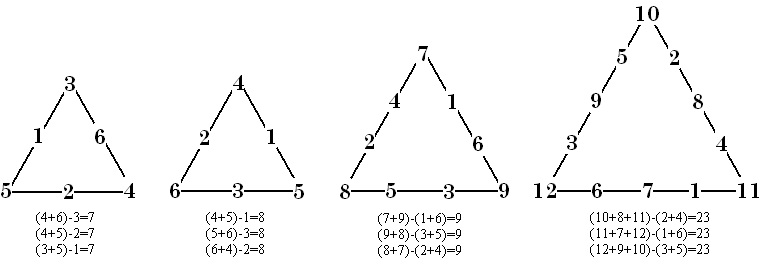
Some questions posed by the author:
Can a subtractive magic triangle be formed from the first 3n natural numbers for
any order > 3?
Does a subtractive magic triangle retain it’s magic property if each element is
increased by a constant?
Does a subtractive magic triangle retain it’s magic property if each element is
multiplied by a constant?
What is the maximum and minimum differences obtainable for subtractive magic
triangles of a given order?
[4] Sunday A. Amose, Subtractive Magic Triangles, Mathematics Teacher, 76 (5), 1983, pp 346-347
![]()
This pattern was suggested by Charles Trigg [5].
The digits 1 to 9 may be partitions into
3 groups, each summing to 15. We can place these groups onto the 3 sides of a
triangle, but with no numbers at the vertices. Thus each side will sum to 15.
There is one group consisting of 2, 2 and 5 integers, eight groups of 3, 3, and
3 integers, and 6 groups of 2, 3, and 4 integers.
I leave it as an exercise for the reader, to find the partitions for the first and last set. Also, how many different unique solutions are possible (don’t count rotations and reflections)?
The eight partitions for 3 sets of 3 are
elegantly represented by the 3 x 3 magic square. The main diagonals cannot be
used because the share the common number 5. The three rows may be placed on the
3 sides of a triangle for one arrangement. The three columns may be placed on
the sides of a triangle for another solution.
Any position is permitted for the numbers on a side, so there are a lot of
possible solutions.
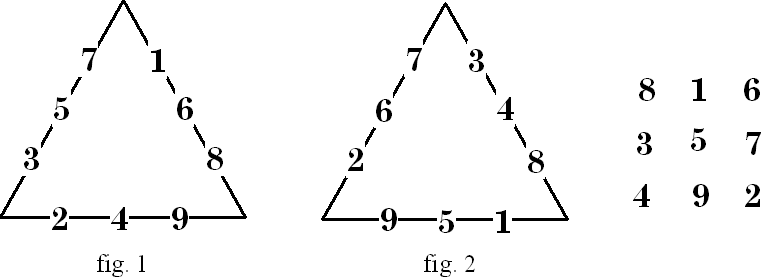 |
Figure 1 is the set represented by the rows of the magic square. Figure 2 is represented by the columns. While this is the simple way to determine which side to place the numbers, there are two other methods (I know of) to do so. Place the numbers on the sides of the triangle in sequence, but at the end of each triad, skip one side (fig 1), or at the end of each triad, place the next number on the same side (fig 2). |
For added interest, this problem may be generalized for polygons of any number of sides.
[5] Charles W. Trigg, Triangles With Balanced Perimeters, Journal of Recreational Mathematics, Vol. 3, No. 4, 1970, pp 255-256
![]()
This digression from perimeter magic triangle, explores another article by Charles Trigg [6]. He investigates formations of numbers arranged in triangular arrays. However, for order 3, these numbers do appear on the perimeter of a triangle (on higher orders, there are interior number as well).
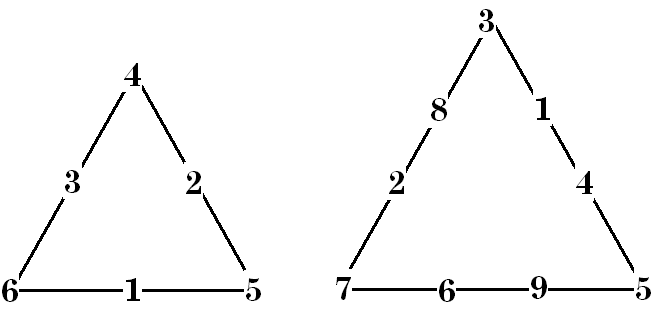 |
Here is one such array were the sums of each side are in consecutive order (ie. 11, 12, 13). As a bonus, the order 2 triangles sums are 8, 9, 10. The inverted order 2, consisting of the 3 mid-side numbers, sum to 6, different but not in consecutive order with the others. A few minutes of doodling produced the order 4 perimeter anti-magic triangle shown. The order 4 side sums are an arithmetic progression order (13, 20, 27). The three order 2 triangles also sum in arithmetic progression order (12, 15, 18). In an order 4 perimeter triangle there is no inverted center triangle. |
In keeping with magic square terminology, these triangles should more properly be called heterotriangles because the sums are different but not in consecutive order. For more in-depth information, see my anti-magic squares page [7]
[6] Charles W.
Trigg, Special Antimagic Triangle Arrays, Journal of Recreational
Mathematics, Vol. 14, No. 4, 1981-82, pp 274-278
[7] For information on anti-magic squares see
http://www.geocities.com/~harveyh/anti_ms.htm
![]()
[1] Terrel Trotter, Jr., Normal Magic Triangles of Order n,
Journal of Recreational Mathematics, Vol. 5,, No. 1, 1972, pp.28-32
[2] Terrel Trotter, Jr., Perimeter-magic Polygons, Journal of
Recreational Mathematics, Vol. 7,, No. 1, 1974, pp.14-20
a scan of his article is at
http://www.trottermath.net/simpleops/pmp.html
[3] John R. Hendricks, The Magic Square Course, 2nd edition,
1992, 522 pages +,
[4] Sunday A. Amose, Subtractive Magic Triangles, Mathematics Teacher, 76
(5), 1983, pp 346-347
[5] Charles W. Trigg, Triangles With Balanced Perimeters, Journal of
Recreational Mathematics, Vol. 3, No. 4, 1970, pp 255-256
[6] Charles W. Trigg, Special Antimagic Triangle Arrays, Journal of
Recreational Mathematics, Vol. 14, No. 4, 1981-82, pp 274-278
[7] For information on anti-magic squares see
http://www.geocities.com/~harveyh/anti_ms.htm
Other related
references:
Yates, Daniel S., Magic Triangles and a Teachers Discovery, Arithmetic
Teacher 23, 1976, pp 351-54.
Lowell A. Carmony, A Minimathematical Problem: The Magic Triangles of Yates,
Mathematics Teacher, 70 (5), 1977, pp. 410-413
Janet Caldwell, Magic Triangles, Mathematics Teacher, 71 (1), 1978, pp.
39-42
Peggy A. House, More Mathemagic from a Triangle, Mathematics Teacher, 73
(3), 1980, pp. 191-195
Charles W. Trigg , Second Order Perimeter–magic and Perimeter-antimagic
Cubes, Mathematics Magazine, 47 (3), 1974, pp95-97
Charles W. Trigg , Edge Magic and Edge Antimagic Tetrahedrons, Journal of
Recreational Mathematics, Vol. 4, No. 4, 1971, pp 253-259
Charles W. Trigg , Edge Magic Tetrahedrons with Rotating Triads, Journal
of Recreational Mathematics, Vol. 5, No. 1, 1972, pp 40-42
Charles W. Trigg, Eight Digits on a Cubes Vertices, Journal of
Recreational Mathematics, Vol. 7, No. 1, 1974, pp 49-75
Charles W. Trigg, Perimeter Antimagic tetrahedrons and Octahedrons,
Journal of Recreational Mathematics, Vol. 11, No. 2, 1978-79, pp 105-107
For information on Perimeter magic cubes see my
http://members.shaw.ca/hdhcubes/cube_unusual.htm#Perimeter-magic
![]()
. Please send me Feedback
about my Web site!
Please send me Feedback
about my Web site!![]()

![]()
![]()
Harvey Heinz harveyheinz@shaw.ca
Last updated November 29, 2006
Copyright © 1999 by Harvey D. Heinz