Hexiamond Compatibility

Introduction

A hexiamond is a plane figure made of six equilateral triangles joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated by T. H. O'Beirne.

The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Polyomino compatibility has been widely studied since the early 1990s. Polyiamond compatibility was first studied systematically by Margarita Lukjanska and Andris Cibulis, who published a paper about it with Andy Liu in 2004 in the Journal of Recreational Mathematics. While the journal was preparing the paper for print, I corresponded with the authors, supplying the missing hexiamond compatibility and some other solutions. My contributions arrived too late to appear in print, but I was listed as a joint author.

This web page and my other page, Mixed Polyiamond Compatibility, extend and correct the solutions in the JRM article. For sets of three hexiamonds, see Triple Hexiamonds.

  • Arbitrary Solutions
  • Odd Variants
  • Thin Variants
  • Holeless Solutions
  • Horizontal Symmetry
  • Holeless with Horizontal Symmetry

    • Arbitrary Solutions

    Table

    This table shows the smallest number of tiles needed to construct a figure tilable by both hexiamonds.

     AEFHILOPSUVX
    A*32323×21832×
    E3*6233×64363
    F26*222622226
    H322*32622233
    I2323*3×2332×
    L33223*623233
    O××66×6*6333×
    P2622226*2222
    S184223332*23×
    U332232322*3×
    V2623233233*×
    X×363×3×2×××*

    Solutions

    These solutions are minimal. They are not necessarily uniquely minimal.

    2 Tiles

    3 Tiles

    4 Tiles

    6 Tiles

    18 Tiles

    Odd Variants

     AEFHILOPSUVX
    A*3×353××3335×
    E3*×333××53153
    F××*××××3××××
    H33×*3333×3533
    I53×3*3××339×
    L33×33*15×3333
    O×××33×15*×333×
    P××3××××*××××
    S335×3333×*33×
    U33×5333×3*3×
    V515×3933×33*×
    X×3×3×3×××××*

    Thin Variants

    These compatibilities are thinner than the corresponding basic solutions. Some use more tiles.

     

    Holeless Solutions

    Table

    This table shows the smallest number of tiles needed to construct a holeless figure tilable by both hexiamonds. Cells shaded in green need the same number of tiles if holes are allowed.

     AEFHILOPSUVX
    A*×2324×2?92×
    E×*322?6×66??×
    F232*222422222×
    H322*42122229×
    I2?24*3×2342×
    L46223*102324×
    O××4212×10*6333×
    P2622226*2222
    S?6223332*23×
    U9?2242322*3×
    V2?29243233*×
    X×××××××2×××*

    Solutions

    These solutions are the smallest known. They are not necessarily uniquely minimal. I show only solutions that differ from the solutions given above.

    4 Tiles

    6 Tiles

    9 Tiles

    10 Tiles

    12 Tiles

    32 Tiles

     

    42 Tiles

     

    Horizontal Symmetry

    Solutions with horizontal symmetry can be hard to find.

    Table

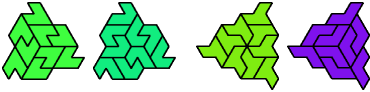
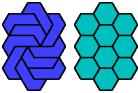
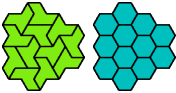
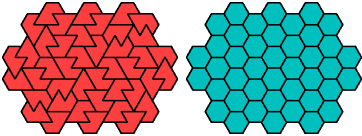
     AEFHILOPSUVX
    A*?6666×6??6×
    E?*?4??×66??×
    F6?*6666630126×
    H646*12666121818×
    I6?612*3×6?36×
    L6?663*661836×
    O××66×6*6181818×
    P6666666*181262
    S?63012?181818*1618×
    U??121833181216*18×
    V6?618661861818*×
    X×××××××2×××*

    Solutions

    Holeless with Horizontal Symmetry

    Table

     AEFHILOPSUVX
    A*×1261232×12??12×
    E×*?4??×????×
    F12?*181284212304212×
    H6418*?183030243030×
    I12?12?*7×10?910×
    L32?8187*101424924×
    O××4230×10*14242424×
    P12?1230101414*242482
    S??3024?242424*2424×
    U??423099242424*24×
    V12?123010242482424*×
    X×××××××2×××*

    Solutions

    Last revised 2023-08-12.

    Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]