

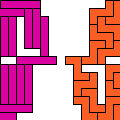
| 
| 
| 
| 
|
| Polyominoes | Polyiamonds | Polyhexes | Other Plane Polyforms | Solid Polyforms |
|---|
 | Pentomino Compatibility. Given two pentominoes, construct a figure that can be tiled with either. |
 | Vertical I-Pentomino Compatibility. Given any polyomino, construct a figure that can be tiled with it and with the I pentomino, using the I pentomino only in vertical orientation. |
 | Holeless Pentomino Odd Pairs. Holeless solutions for Livio Zucca's Pentomino Odd Pairs. |
 | Pentomino Pair-Single Compatibility. Joint compatibility for two pentominoes with a third. |
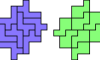 | Holeless Hexomino Compatibility. Given two hexominoes, construct a holeless figure that can be tiled with either. |
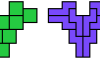 | Tetromino-Pentomino Compatibility. Given a tetromino and a pentomino, construct a figure that can be tiled with either. |
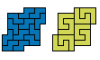 | Holeless Tetromino-Hexomino Compatibility. Given a tetromino and a hexomino, construct a holeless figure that can be tiled with either. |
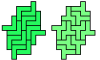 | Holeless Pentomino-Hexomino Compatibility. Given a pentomino and a hexomino, construct a holeless figure that can be tiled with either. |
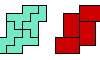 | 2×3 Hexomino Compatibility. Which polyominoes are compatible with the 2×3 rectangular hexomino? |
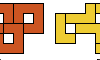 | Holey Heptomino Compatibility. Which polyominoes are compatible with the holey heptomino? |
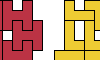 | H Heptomino Compatibility. Which polyominoes are compatible with the H heptomino? |
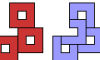 | Voided Square Octomino Compatibility. Which polyominoes are compatible with the square octomino with a hole in it? |
 | Pinwheel Octomino Compatibility. Which polyominoes are compatible with the pinwheel octomino? |
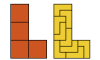 | Square Enneomino Compatibility. Which polyominoes are compatible with the square enneomino? |
 | A Euphoric Heptomino. This heptominoes is compatible with every polyomino of order 6 or less. |
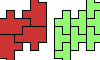 | Two Euphoric Octominoes. Two octominoes are compatible with every polyomino of order 6 or less. |
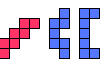 | Minimal Incompatibility for Polyominoes. What are the smallest polyominoes that are not compatible with a given polyomino? |
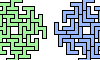 | Addendum to Polypolyominoes. New and smaller polyomino compatibilities for Giovanni Resta's Polypolyominoes. |
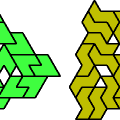
 | Pentiamond Compatibility. Given two pentiamonds, construct a figure that can be tiled with either. |
 | Hexiamond Compatibility. Given two hexiamonds, construct a figure that can be tiled with either. |
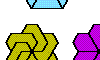 | Heptiamond Compatibility. Given two heptiamonds, construct a figure that can be tiled with either. |
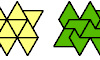
| Mixed Polyiamond Compatibility. Given two polyiamonds of different orders, construct a figure that can be tiled with either. |
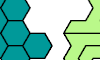
| Hexagon Hexiamond Compatibility. Find a figure that can be tiled with a given polyiamond and with the Hexagon hexiamond. |
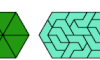
| Triangle Enneiamond Compatibility. Find a figure that can be tiled with a given polyiamond and with the triangular enneiamond. |
 | Minimal Incompatibility for Polyiamonds. What are the smallest polyiamonds that are not compatible with a given polyiamond? |
 | Pentahex Compatibility. Given two pentahexes, construct a figure that can be tiled with either. |
 | Pentahex Odd Pairs. Given two pentahexes, construct a figure that can be tiled with an odd number of either. |
 | Mixed Polyhex Compatibility. Given two polyhexes of different sizes, find a polyhex that can be tiled with either. |
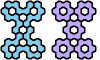 | Seven Euphoric Pentahexes. Each of these pentahexes is compatible with all 82 hexahexes. |
 | Three Euphoric Hexahexes. Each of these hexahexes is compatible with all 82 hexahexes. |
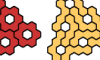 | Ring Hexahex Compatibility. Which polyhexes are compatible with the ring hexahex? |
 | Disk Heptahex Compatibility. Which polyhexes are compatible with the disk heptahex? |
 | Minimal Incompatibility for Polyhexes. What are the smallest polyhexes that are not compatible with a given polyhex? |
 | Tripent-Tetrapent Compatibility. Figures that can be tiled by a given tripent and tetrapent. |
 | Tripent-Pentapent Compatibility. Figures that can be tiled by a given tripent and pentapent. |
 | Tetrapent-Pentapent Compatibility. Figures that can be tiled by a given tetrapent and pentapent. |
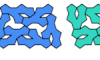 | Pentapent Compatibility. Figures that can be tiled by two different pentapents. |
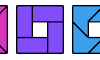 | Tetrabolo Compatibility. Given two tetraboloes, construct a figure that can be tiled with either. |
 | Pentabolo Compatibility. Given two pentaboloes, construct a figure that can be tiled with either. |
 | Pentabolo Odd Pairs. Given two pentaboloes, construct a figure that can be tiled with an odd number of either. |
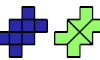 | Diabolo-Tetrabolo Compatibility. Given a diabolo and a tetrabolo, construct a figure that can be tiled with either. |
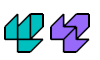 | Triabolo-Tetrabolo Compatibility. Given a triabolo and a tetrabolo, construct a figure that can be tiled with either. |
 | Tetrabolo-Pentabolo Compatibility. Given a tetrabolo and a pentabolo, construct a figure that can be tiled with either. |
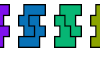 | Tetrahop Compatibility. Given two tetrahops, construct a figure that can be tiled with either. |
 | Didrafter Compatibility. Given two didrafters, construct a figure that can be tiled with either. |
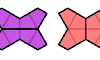 | Tetrakite Compatibility. Given two tetrakites, construct a figure that can be tiled with either. |
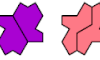 | Trigem Compatibility. Given two trigems, construct a figure that can be tiled with either. |
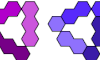 | Trihing Compatibility. Given two trihings, construct a figure that can be tiled with either. |
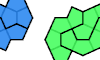 | Tetracairo Compatibility. Given two tetracairos, construct a figure that can be tiled with either. |
 | Dicrown Compatibility. Given two dicrowns, construct a figure that can be tiled with either. |
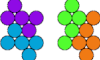 | Pentapenny Compatibility. Given two pentapennies, construct a figure that can be tiled with either. |
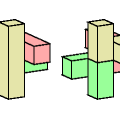
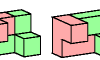 | Tetracube Compatibility. Given two tetracubes, construct a figure that can be tiled with either. |
 | Pentacube Compatibility. Given two pentacubes, construct a figure that can be tiled with either. |
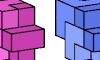 | Pentacube Odd Pairs. Given two pentacubes, construct a figure that can be tiled with either, using an odd number of each. |
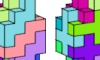 | Flat Hexacube Compatibility. Given two solid hexominoes, construct a figure that can be tiled with either. |
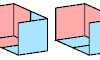 | Triominoid Compatibility. Given two triominoids, construct a figure that can be tiled with either. |