Tetrabolo Compatibility

Introduction

A tetrabolo is a figure made of four equal isosceles right triangles joined at equal edges. There are 14 such figures, not distinguishing reflections and rotations.

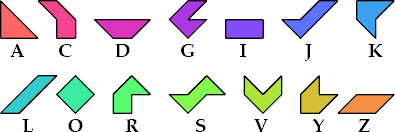
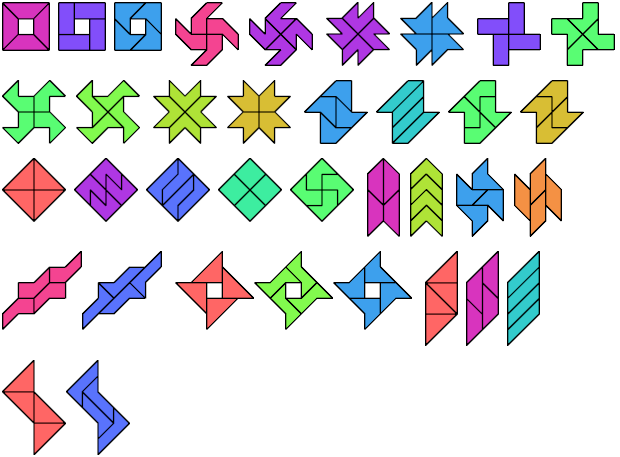
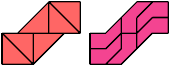
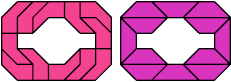
Here are minimal compatibility figures for tetraboloes. Not all are uniquely minimal. They first appeared in Erich Friedman's Math Magic for September 2004, and Dr. Friedman found all but the three largest.

Summary

I adopt Dr. Friedman's nomenclature:

 ACDGIJKLORSVYZ
A*6442422444××2
C6*124×42××2××××
D412*24224×2×4×2
G442*×2422222××
I2×4×*×4××4××××
J4422×*222422××
K222442*4×441624
L2×42×24*×4××22
O4××2×2××*4××××
R422244444*4×4×
S4××2×24××4*×××
V××42×216××××*42
Y××××××22×4×4*×
Z2×2×××42×××2×*

2 Tiles

4 Tiles

6 Tiles

12 Tiles

16 Tiles

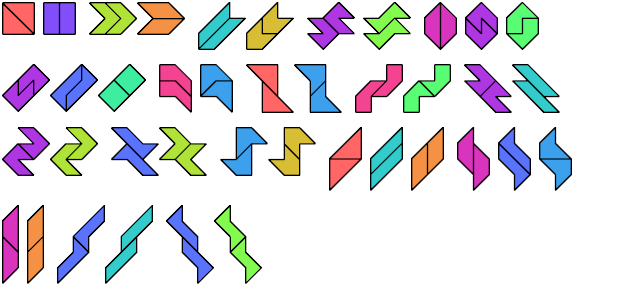
Last revised 2013-10-08.

Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]