



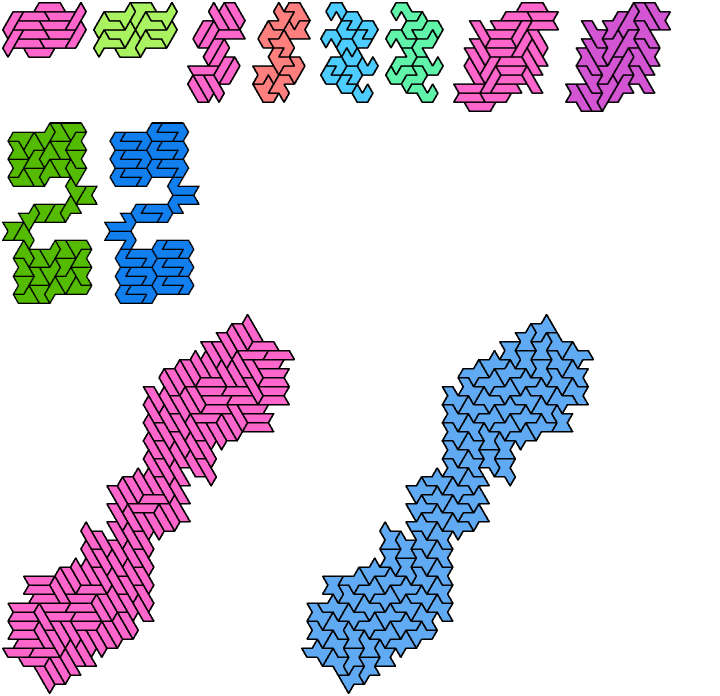
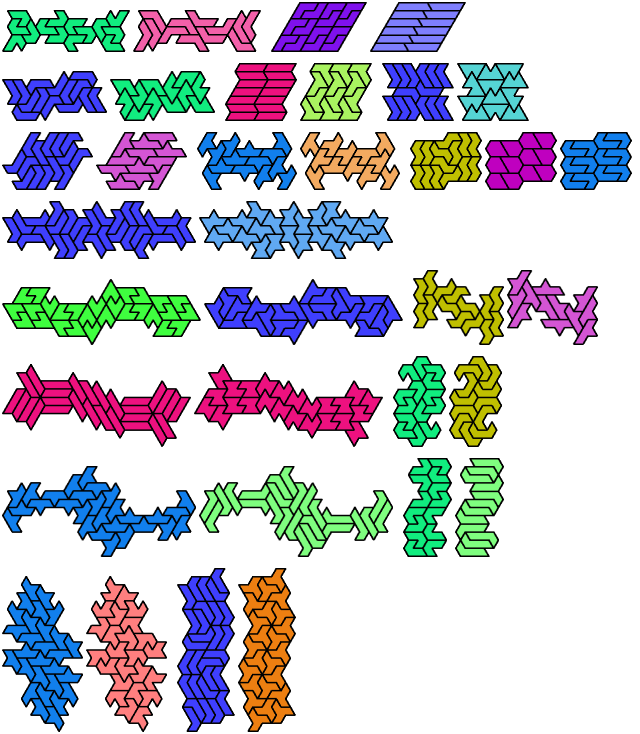
See also Hexiamond Compatibility and Heptiamond Compatibility.
 |  |  | |
|---|---|---|---|
 | 3:4 | 3:4 | 3:4 |



 |  |  |  | |
|---|---|---|---|---|
 | 3:5 | 3:5 | 3:5 | 3:5 |


 |  |  |  | |
|---|---|---|---|---|
 | 8:10 | 8:10 | 8:10 | — |
 | 4:5 | 4:5 | 4:5 | 4:5 |
 | 4:5 | 4:5 | 4:5 | 4:5 |
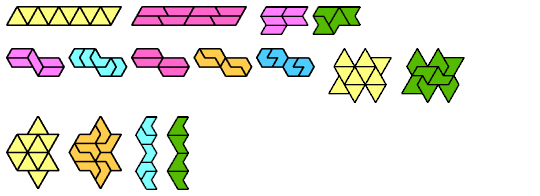

 |  |  |  |  |  |  |  |  |  |  |  | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | 2:4 | 1:2 | 2:4 | 1:2 | 1:2 | 1:2 | 1:2 | 1:2 | 1:2 | 1:2 | 1:2 | 3:6 |





| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

| 5:7 | 10:14 | 5:7 | 10:14 | 10:14 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 15:21 | 5:7 |

| 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 10:14 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 |

| 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 10:14 | 5:7 | 5:7 |

| 10:14 | 15:21 | 20:28 | ? | 30:42 | 5:7 | 40:56 | 10:14 | 30:42 | 5:7 | ? | ? |

| 
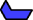
| 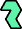
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

| 10:14 | 10:14 | 10:14 | 5:7 | 5:7 | 10:14 | 5:7 | 5:7 | 20:28 | 10:14 | 5:7 | 10:14 |

| 10:14 | 5:7 | 5:7 | 10:14 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 | 5:7 |

| 5:7 | 5:7 | 10:14 | 5:7 | 5:7 | 5:7 | 5:7 | 10:14 | 15:21 | 10:14 | 5:7 | 5:7 |

| ? | 60:84 | 5:7 | 10:14 | 10:14 | 10:14 | 20:28 | 15:21 | ? | ? | 5:7 | 5:7 |



| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

| 24:28 | 6:7 | 12:14 | 12:14 | 12:14 | 12:14 | 6:7 | 12:14 | 12:14 | 24:28 | 36:42 | 12:14 |

| 12:14 | 12:14 | 6:7 | 12:14 | 12:14 | 12:14 | 12:14 | 6:7 | 6:7 | 12:14 | 36:42 | 6:7 |

| 6:7 | 6:7 | 12:14 | 12:14 | 6:7 | 12:14 | 6:7 | 6:7 | 12:14 | 12:14 | 6:7 | 12:14 |

| 12:14 | 12:14 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 6:7 |

| 12:14 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 6:7 | 6:7 | 12:14 | 6:7 |

| 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 6:7 | 12:14 | 12:14 | 6:7 | 12:14 | 12:14 | 12:14 |

| 6:7 | ? | ? | 6:7 | ? | ? | ? | 6:7 | ? | ? | ? | ? |

| 12:14 | 6:7 | 6:7 | 12:14 | 6:7 | 12:14 | 6:7 | 6:7 | 6:7 | 12:14 | 12:14 | 6:7 |

| 6:7 | 12:14 | 12:14 | 6:7 | 6:7 | 12:14 | 12:14 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 |

| 6:7 | 12:14 | 6:7 | 12:14 | 6:7 | 12:14 | 6:7 | 6:7 | 12:14 | 6:7 | 36:42 | 12:14 |

| ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |

| 18:21 | 24:28 | 12:14 | 72:84 | 6:7 | 6:7 | 12:14 | 12:14 | 54:63 | ? | 6:7 | 36:42 |

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

| 24:28 | 12:14 | 24:28 | 12:14 | 12:14 | 12:14 | 12:14 | ? | ? | ? | 12:14 | 12:14 |

| 12:14 | 12:14 | 12:14 | 36:42 | 12:14 | 6:7 | 12:14 | 12:14 | ? | ? | 12:14 | 12:14 |

| 18:21 | 12:14 | 12:14 | 12:14 | 6:7 | 6:7 | 6:7 | 12:14 | 48:56 | 12:14 | 6:7 | 6:7 |

| 6:7 | 12:14 | 36:42 | 12:14 | 6:7 | 6:7 | 6:7 | 36:42 | 6:7 | ? | 6:7 | 12:14 |

| 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 6:7 | 6:7 |

| 6:7 | 6:7 | 12:14 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 24:28 | 12:14 | 12:14 | 6:7 |

| ? | ? | 6:7 | ? | ? | 6:7 | 6:7 | 6:7 | ? | 6:7 | ? | 6:7 |

| 6:7 | 12:14 | 12:14 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 36:42 | 6:7 | 6:7 | 12:14 |

| ? | 36:42 | 6:7 | 6:7 | 12:14 | 6:7 | 6:7 | 6:7 | ? | 6:7 | 12:14 | 6:7 |

| ? | 6:7 | 6:7 | 12:14 | 6:7 | 6:7 | 6:7 | 6:7 | 6:7 | 12:14 | 12:14 | 12:14 |

| ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |

| ? | ? | 12:14 | 36:42 | 12:14 | 12:14 | 12:14 | 18:21 | ? | 12:14 | 6:7 | 12:14 |



Last revised 2024-11-10.