Minimal Incompatibility for Polyominoes
Introduction
A polyomino is a figure made of equal squares joined
edge to edge.
Polyominoes were first enumerated and studied by Solomon Golomb.
The compatibility problem
is to find a figure that can be tiled with each of a set of polyforms.
Here I show for each polyomino of orders 1 through 6 the smallest known
polyominoes that are not compatible with it.
In most cases, incompatibility is probable but has not been proved
by analysis or exhaustion.
Proved cases are shown in red. Unproved cases are shown in blue.
Giovanni Resta showed that the L tetromino is compatible with
all polyominoes of order 10 or less, and found minimal incompatibilies
for many other polyominoes.
His site Polipolimini
is out and away the best place to find polyomino compatibilities.
Andris Cibulis first studied domino compatibility
and found the minimal polyominoes incompatible with the domino.
He also eliminated many 11-ominoes for the L tetromino
by finding complex compatibility figures for them.
Juris Čerņenoks found complex compatibility figures for two
11-ominoes with the L tetromino.
Thanks to Erich
Friedman for suggesting this page.
See also Minimal Incompatibility for Polyiamonds
and Minimal Incompatibility for Polyhexes.
Solutions
| Monomino |
|---|
 | ∞ | None |
| Domino |
|---|
 | 13 | 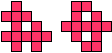 |
| Trominoes |
|---|
 | 5 | 
|  | 9 |  |
| Tetrominoes |
|---|
 | 5 | 
|  | 11 | 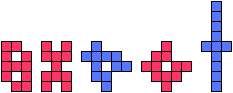 |
 | 7 | 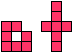
|  | 7 | 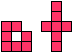 |
 | 5 |  |
| Pentominoes |
|---|
 | 5 | 
|  | 7 |  |
 | 8 | 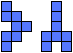
|  | 7 | 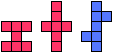 |
 | 5 | 
|  | 7 |  |
 | 5 | 
|  | 7 | 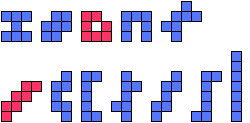 |
 | 8 | 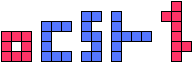
|  | 5 |  |
 | 5 | 
|  | 3 |  |
| Hexominoes |
|---|
 | 5 | 
|  | 5 |  |
 | 7 | 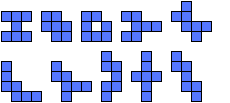
|  | 5 |  |
 | 5 | 
|  | 5 |  |
 | 5 | 
|  | 5 |  |
 | 5 | 
|  | 5 |  |
 | 5 | 
|  | 7 |  |
 | 7 | 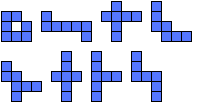
|  | 5 |  |
 | 5 | 
|  | 5 |  |
 | 4 | 
|  | 7 |  |
 | 7 | 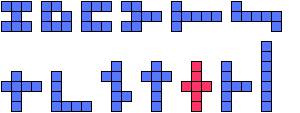
|  | 4 |  |
 | 7 | 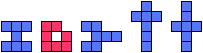
|  | 5 |  |
 | 5 | 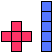
|  | 7 | 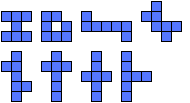 |
 | 5 | 
|  | 7 | 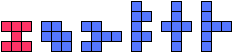 |
 | 5 | 
|  | 4 |  |
 | 5 | 
|  | 5 |  |
 | 5 | 
|  | 4 |  |
 | 4 | 
|  | 4 | 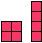 |
 | 4 |  |
Last revised 2015-04-29.
Back to Pairwise Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]














































































































