Flat Hexacube Compatibility

Introduction

A hexacube is a solid made of six cubes joined face to face. A solid hexomino, or flat hexacube, is a hexacube whose cells lie all in one plane. As there are 35 hexominoes, there are 35 flat hexacubes:

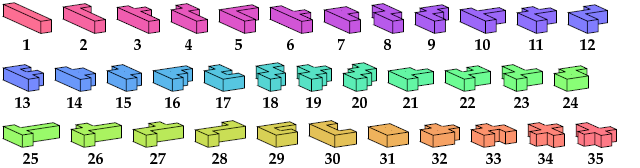
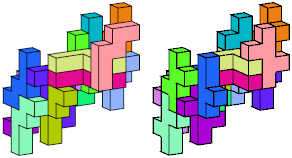
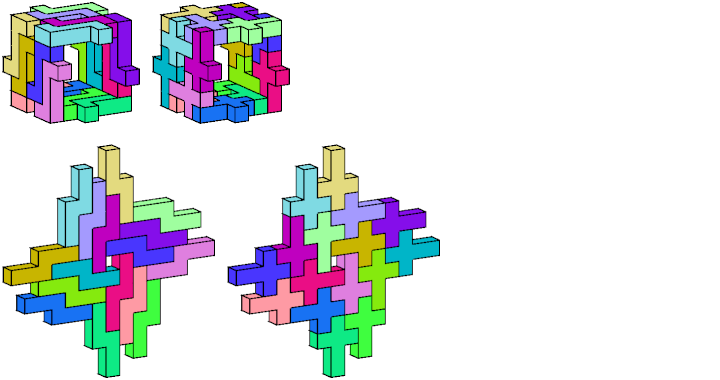
Two or more polyforms are compatible if there is a polyform that each can tile. Most pairs of hexominoes are compatible, but many are not; see Giovanni Resta's page Hexominoes. All but one pair of flat hexacubes are known to be compatible:

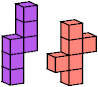
If you solve this case, or find a smaller solution for another case, please write.

Thanks to Mark Smith for suggesting this problem.

Table of Tiles

This table shows how many tiles are needed to demonstrate compatibility of two flat hexacubes. Green cells indicate that the number is equal to that for the corresponding hexominoes. Purple cells indicate that no solution is known for the corresponding hexominoes.

 1234567891011121314151617181920212223242526272829303132333435
1•2224222444442244463446346664626366
22•222224222224422243222222222224448
322•22244222222224426224622222442622
4222•24242222222222222222234422342108
54222•423222222224443264422422226668
622244•22424244484286262242242438622
7224222•2224222424223222244432222334
82444322•2422442424232424244424266?16
942222422•224442422222242624422344148
10422222242•2222444466222422423236642
114222244222•224242426424442262842222
1242222222422•484422432222622222243410
13422224244224•2222222224224222223222
142422242442482•224422248283444232244
1524222442242422•222262244484644236124
16422228244444222•4822248426282824488
174242444224222424•224223342242444342
1842424224244224282•23222382222422424
19642248222624222222•2222244244242224
203362363326632262432•2664644364322610
2142222222224222222222•22222422222424
22422266242222242422262•2224282644284
236242422242424848322622•242423244422
2432624224244222443324222•42244242446
25422224426246284248462244•22244246124
266223224422224386224424222•224342222
2762244244442224422224424222•24444622
28622424344262246842432824222•24326616
294222222223222442224622344442•226486
3062422424228222484424262243442•34648
31224323223342232242432444244323•4366
326424682646243234422224424242644•242
3334626636462322643422424462664632•44
3464210623?1442424128422628241222684644•2
3568288241682210244824410442642216686242•
 1234567891011121314151617181920212223242526272829303132333435

Solutions

There are 595 cases, too many to show here. Instead I show only solutions with at least 10 tiles. The flat solution is from Resta's page.

10 Tiles

12 Tiles

14 Tiles

16 Tiles

Last revised 2024-07-08.

Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]