Pentapenny Compatibility

Introduction

A pentapenny is a plane figure formed by joining five equal discs tangentially. Two pentapennies are considered the same if there is a topological homeomorphism of the plane that converts one to the other. By this criterion there are 13 different pentapennies:

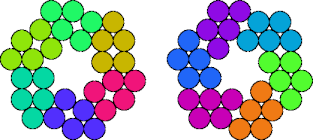
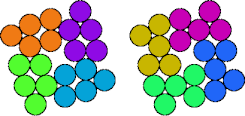
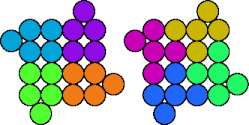
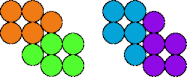
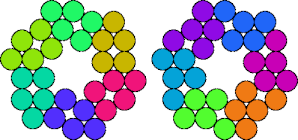
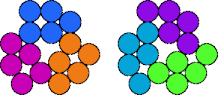
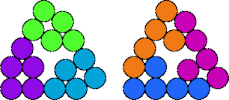
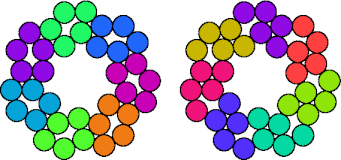
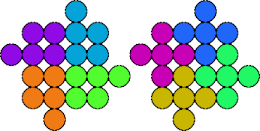
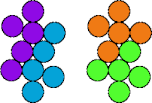
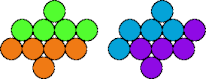
Two pentapennies are compatible if there is a polypenny that can be completely tiled by either. Here I show minimal known compatibility figures for pairs of pentapennies.

If you find a smaller solution or solve any of the unsolved cases, please let me know.

For enumeration of polypennies see Catalogue of Polypennies.

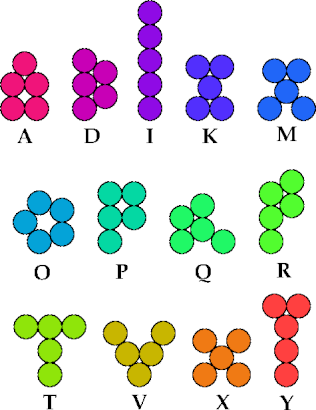
  ADIKMOPQRTVXY
A*6244?26332?2
D6*236?62242?2
I22*3222222262
K433*2??2232?2
M4622*74242222
O??2?7*77744?4
P262?47*432242
Q6222274*222?2
R32224732*22?2
T342324222*222
V2222242222*?2
X??6?2?4??2?*?
Y22222422222?*

5A—5D5A—5I5A—5K5A—5M
5A—5O5A—5P5A—5Q5A—5R
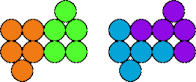
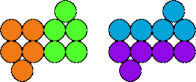
5A—5T5A—5V5A—5X5A—5Y
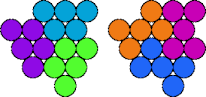
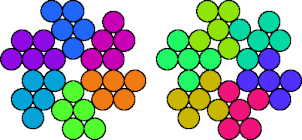
5D—5I5D—5K5D—5M5D—5O
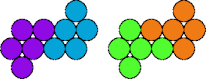
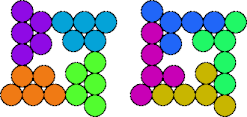
5D—5P5D—5Q5D—5R5D—5T
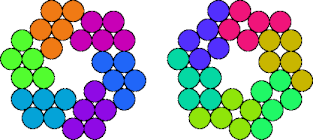
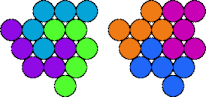
5D—5V5D—5X5D—5Y5I—5K
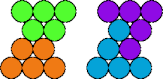
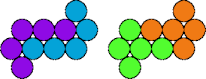
5I—5M5I—5O5I—5P5I—5Q
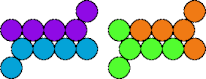
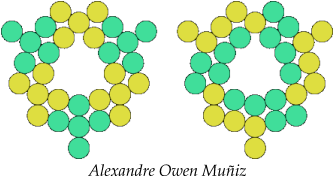
5I—5R5I—5T5I—5V5I—5X
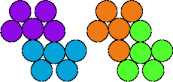
5I—5Y5K—5M5K—5O5K—5P
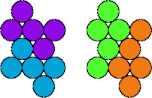
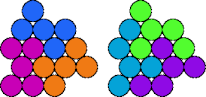
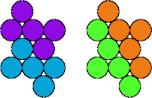
5K—5Q5K—5R5K—5T5K—5V
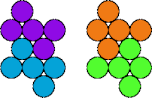
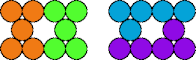
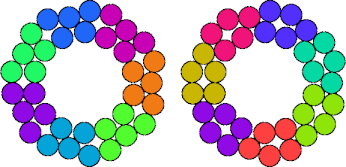
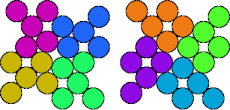
5K—5X5K—5Y5M—5O5M—5P
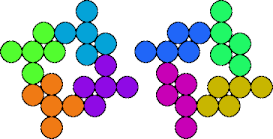
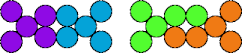
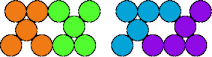
5M—5Q5M—5R5M—5T5M—5V
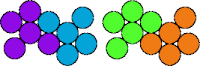
5M—5X5M—5Y5O—5P5O—5Q
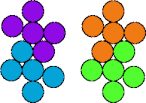
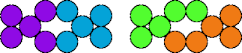
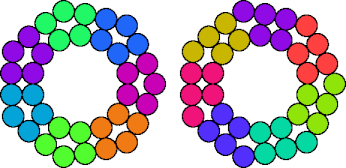
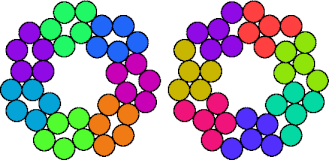
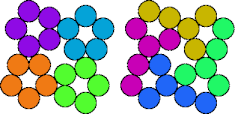
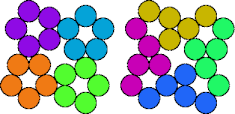
5O—5R5O—5T5O—5V5O—5X
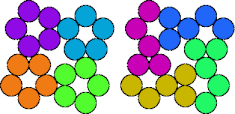
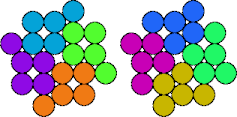
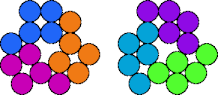
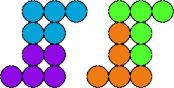
5O—5Y5P—5Q5P—5R5P—5T
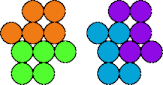
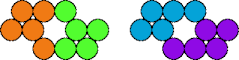
5P—5V5P—5X5P—5Y5Q—5R
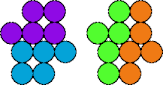
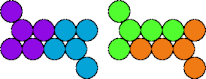
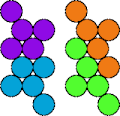
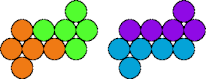
5Q—5T5Q—5V5Q—5X5Q—5Y
5R—5T5R—5V5R—5X5R—5Y
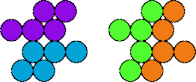
5T—5V5T—5X5T—5Y5V—5X
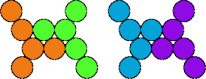
5V—5Y5X—5Y

Last revised 2020-04-01.

Back to Polyform Compatibility < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]