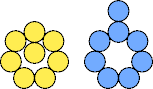
Polypennies may also be distinguished by internal homeomorphism without reference to the plane. Alexandre Owen Muñiz gives this example of two homeomorphic polypennies that are not homeomorphically embedded in the plane:

Polypennies may also be distinguished by isomorphism of their adjacency graphs without respect to the cyclical sequence of adjacencies at each node. These polypennies have isomorphic adjacency graphs and are not internally homeomorphic:
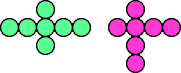
This page shows all free polypennies of orders 1–6. Erich Friedman enumerated all polypennies up to order 4. Alexandre Owen Muñiz enumerates polypennies up to order 5 on Flexible Polyforms at his site Math at First Sight.
The On-Line Encyclopedia of Integer Sequences enumerates connected penny graphs (not polypennies) up to order 8 as sequence A085632.
| Order | Free | One-Sided |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 5 | 5 |
| 5 | 13 | 13 |
| 6 | 46 | 57 |