

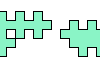 | Catalogue of Unitary Polyominoes. A unitary polyomino is one whose edges all have length 1. |
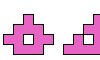 | Catalogue of Almost Unitary Polyominoes. An almost unitary polyomino is one whose edges all but one have length 1. |
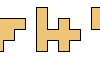 | Catalogue of Almost Almost Unitary Polyominoes. An almost almost unitary polyomino is one whose edges all but two have length 1. |
 | Catalogue of Unitary Polyiamonds. A unitary polyiamond is one whose edges all have length 1. |
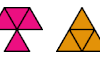 | Catalogue of Polymings. A polyming is a generalization of a polyiamond in which cells may be joined at corners as well as at edges. |

| Database of Convex Polyaboloes.
A tarballof all convex polyaboloes with up to 800 cells. |

| Catalogue of Blunt Polytans. A blunt polytan is one with no 45° corners. |

| Catalogue of Tetrakis Polyaboloes. A tetrakis polyabolo is one that conforms to the Tetrakis Grid. |
| Catalogue of Polyfetts. A polyfett is a generalized polyabolo whose cells may be joined at edges or at vertices. |
| Catalogue of Convex Polydrafters. |

| Catalogue of Didrifters. |
| Catalogue of Polykagomes. A polykagome is a polyform defined on the trihexagonal grid. |
| Catalogue of Polybirds. A polybird is a polyform defined on the rhombitrihexagonal grid. |
 | Catalogue of Polyhops. Thomas Atkinson's hopscotch-style polyominoes. |
 | Catalogue of Polyjogs. Polyforms formed of squares joined by half edges. |
 | Catalogue of Polynars. László Molnár's shapes formed of squares joined by edges and half edges. |
 | Catalogue of Polyhings. Polyforms formed of regular hexagons joined edge to edge or at vertices in parallel. |
 | Catalogue of Polybrexes. Polyforms formed of regular hexagons joined edge to edge or separated by the length of an edge. |
 | Catalogue of Polypents. Enumerations and pictures of these neglected polyforms. |
 | Catalogue of Cyclic Polypents. Polypents whose cells form a closed loop. |
 | Figure Eight Polypent Loops. Generalized polypents that cross themselves to form a loop in the shape of a figure eight. |
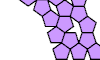 | Unique Polypents With Full Symmetry and Minimum Perimeter. Polypents with full symmetry and the uniquely least possible perimeter for their area. |
 | Unique Polypents With Star Symmetry and Minimum Perimeter. Polypents with star symmetry and the uniquely least possible perimeter for their area. |
 | Catalogue of Polyhepts. Some more neglected polyforms. |
 | Catalogue of Cyclic Polyhepts. Polyhepts whose cells form a closed loop. |
 | Catalogue of Polyocts. Still more neglected polyforms. |
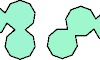 | Catalogue of Polyenns. Highly neglected polyforms. |
 | Catalogue of Cyclic Polyenns. Polyenns whose cells form a closed loop. |
 | Catalogue of Polypexes. Polyforms whose base cell is an equilateral hexagon with angles 72°–144°–144°–72°–144°–144°. |
 | Catalogue of Polypentagrams. Polyforms formed of pentagrams joined edge to edge. |
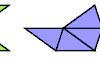 | Catalogue of Polygolds. Polyforms formed by joining golden triangles at equal edges. |
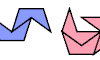 | Catalogue of Polycrowns. Polyforms formed of collapsed regular pentagons joined edge to edge. |
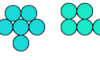 | Catalogue of Polypennies. Polyforms formed by joining equal disks tangentially. |
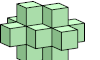 | Catalogue of Unitary Polycubes. Polycubes whose faces are all monominoes. |
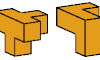 | Catalogue of Besźel Polycubes. Polycubes whose cells have a preponderance of even coordinates. |
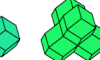 | Catalogue of Polyrhons. Polyforms formed by joining rhombic dodecahedrons. |
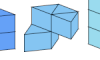 | Catalogue of Polyprisms. Polyforms formed by joining equilateral-triangular prisms. |
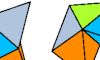 | Catalogue of Polytets. Polyforms formed by joining platonic tetrahedra face to face. |
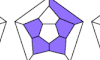 | Catalogue of Polypents on the Surface of a Dodecahedron. |
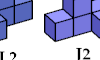 | Pentacube Nomenclature. Various systems for naming the 29 pentacubes. |
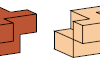 | Polycube Symmetries. In how many ways can a polycube be symmetrical? |
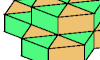 | Polyprism Symmetries. In how many ways can a polyprism be symmetrical? |
 | Catalogue of Polykedges. A polykedge is a polyform formed by joining equal cubes at faces or edges or both. |
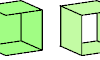 | Catalogue of Polyominoids. A polyominoid is a polyform formed by joining square cells in the polycube grid. |