 A polyomino is a figure made of equal squares joined
edge to edge.
A unitary polyomino is one whose edges all have length 1.
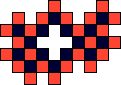
If we color the cells of a unitary polyomino with red and black checks,
all cells on each boundary will have the same color.
In the example at the right, the cells on the outer boundary are all red,
and the cells on the boundary of the hole are all black.
A polyomino is a figure made of equal squares joined
edge to edge.
A unitary polyomino is one whose edges all have length 1.
If we color the cells of a unitary polyomino with red and black checks,
all cells on each boundary will have the same color.
In the example at the right, the cells on the outer boundary are all red,
and the cells on the boundary of the hole are all black.
See also Catalogue of Almost Unitary Polyominoes, Catalogue of Unitary Polyiamonds, and Catalogue of Unitary Polycubes.
| Cells | 1 | 5 | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unitary Polyominoes A245620 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 7 | 10 | 17 | 28 | 47 | 69 |
| Holeless Unitary Polyominoes A245660 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 4 | 5 | 4 | 12 | 13 | 20 | 29 |
In 2023, John Mason continued the enumeration of holeless unitary polyominoes to 50 cells. See the link above.














Last revised 2023-05-01.