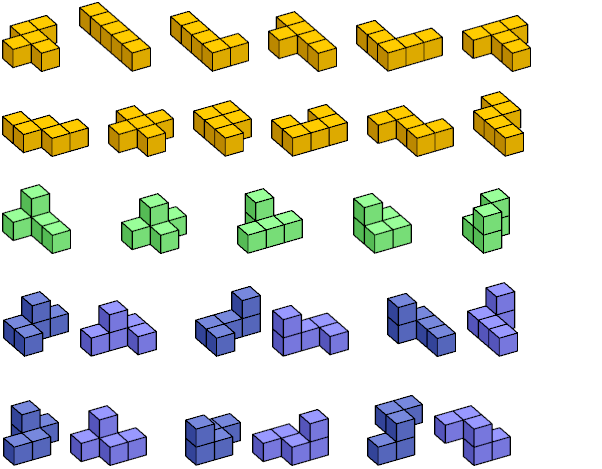
In 1939 the Fairy Chess Review published as Problem 3930 an inquiry by W. D. Rawlings of Pointe Claire, P.Q., Canada: in how many ways can five equal cubes be joined face to face?
The next year, in Volume 4, Number 5 (April 1940), the editor reported that R. J. French had proved that there are 23 such shapes, counting mirror images as the same shape.
In working with sets of pentacubes, mirror images are usually distinguished, since one image cannot be repositioned to make the other. The Fairy Chess Review reported in 1948 that F. Hansson and others had counted 29 pentacubes, counting mirror images as distinct. Some investigators have counted 30, overlooking the plane diagonal mirror symmetry of one of the nonflat pentacubes.
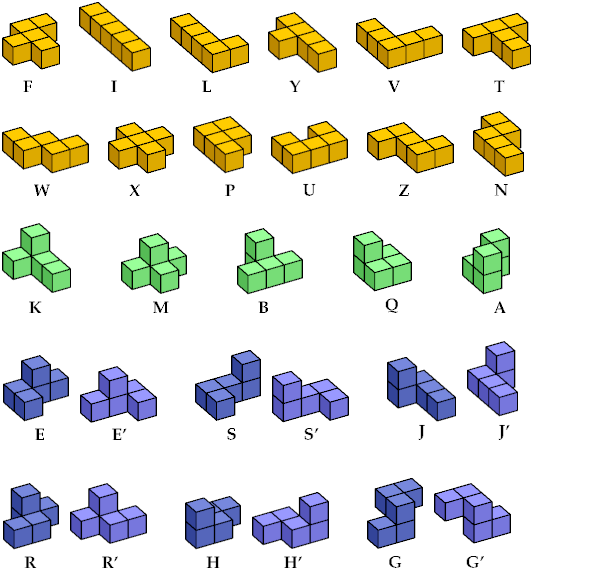
Here are the 29 pentacubes. The flat pentacubes appear first, then the nonflat pentacubes with mirror symmetry, then the six mirror pairs.

The 29 pentacubes have no generally accepted system of names. Below I describe some published ones. If you know of others, please let me know.
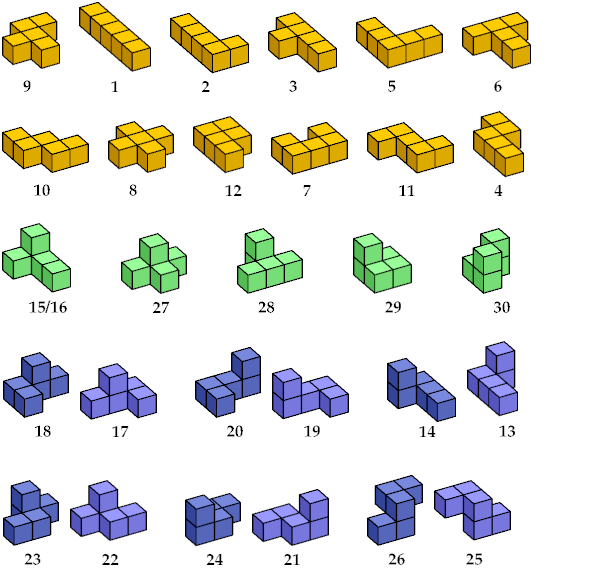
Later Kate produced Super Quintillions®,
an expansion set
for Quintillions.
It contains 18 non-flat pentacubes, one of each of the 17,
and an extra copy of the pentacube labeled J3/L3.
Since 29 is a prime number, there are advantages to having 30 pentacubes.
Kate's system names the solid pentominoes after
Solomon's
Golomb's names
for the pentominoes.
Most of the other names come from the names of solid tetrominoes
that they contain.
A number is added to tell which cell of the tetracube has a bump.
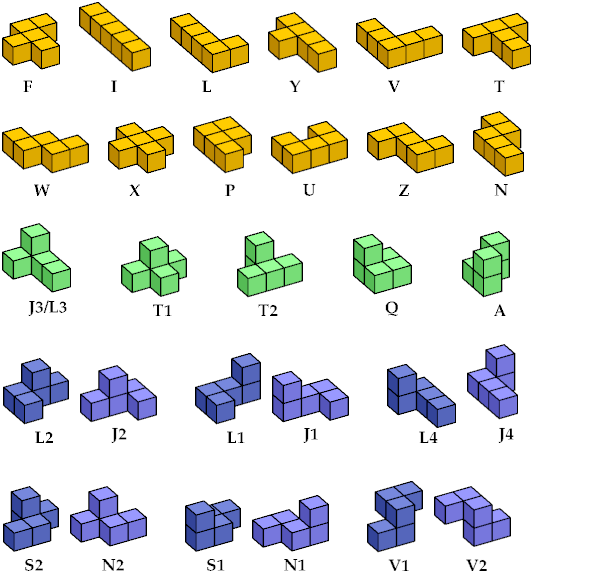
Torsten Sillke described Kate's system as human-friendly.
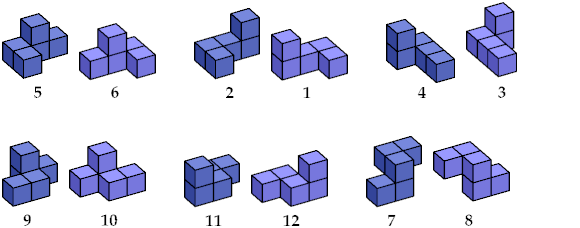
One article, by mathematician Christoffel Bouwkamp,
is called Packing Handed Pentacubes.
It deals only with the 12 chiral pentacubes.
Bouwkamp numbered them as shown:
Knuth's system names the flat pentacubes after John Conway's names for the pentominoes. They are the letters from O to Z inclusive, which is convenient for programming. Knuth uses lower-case letters for the same reason, except that for chiral pairs of pentacubes he uses upper-lower-case pairs of letters:
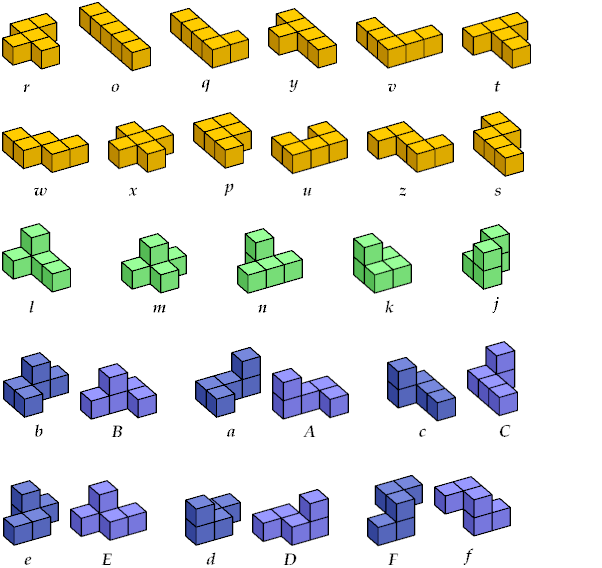
In those days I usually identified mirror images, so I had only 23 pentacubes to name. Naturally I used Roman letters. Later I distinguished chiral pairs by using a prime mark (′):
| Besley | 9 | 1 | 2 | 4 | 12 | 6 | 7 | 5 | 10 | 8 | 3 | 11 | 30 | 28 | 15/16 | 27 | 29 | 18 | 17 | 20 | 19 | 14 | 13 | 23 | 22 | 24 | 21 | 26 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jones | F | I | L | N | P | T | U | V | W | X | Y | Z | A | T2 | J3/L3 | T1 | Q | L2 | J2 | L1 | J1 | L4 | J4 | S2 | N2 | S1 | N1 | V1 | V2 |
| Bouwkamp | 5 | 6 | 2 | 1 | 4 | 3 | 9 | 10 | 11 | 12 | 7 | 8 | |||||||||||||||||
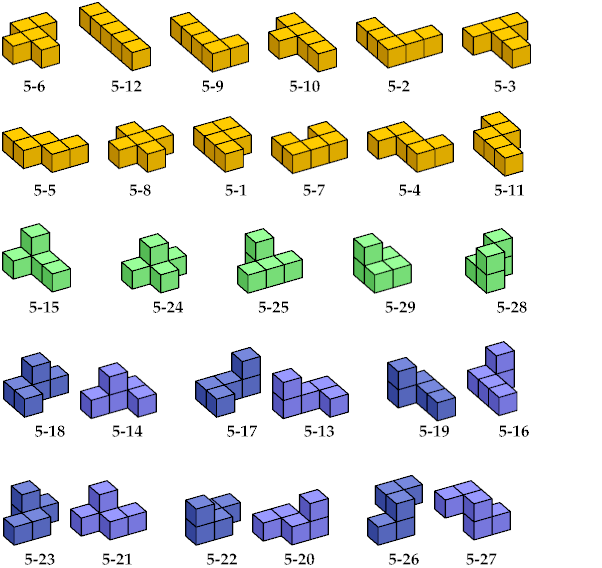
| Coffin | 5-6 | 5-12 | 5-9 | 5-11 | 5-1 | 5-3 | 5-7 | 5-2 | 5-5 | 5-8 | 5-10 | 5-4 | 5-28 | 5-25 | 5-15 | 5-24 | 5-29 | 5-18 | 5-14 | 5-17 | 5-13 | 5-19 | 5-16 | 5-23 | 5-21 | 5-22 | 5-20 | 5-26 | 5-27 |
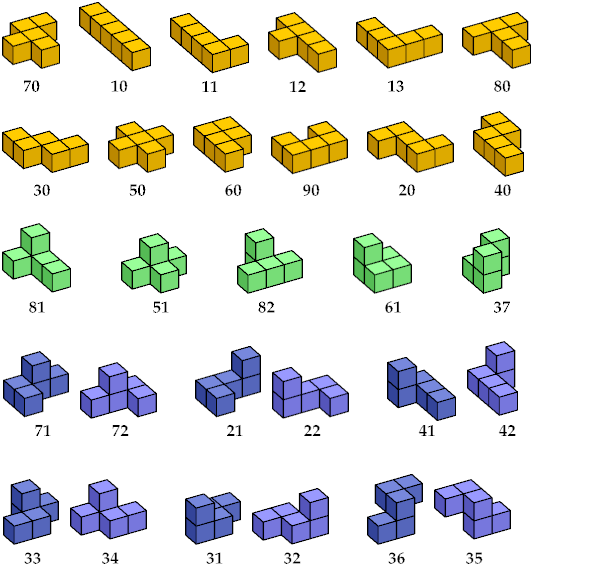
| Künzell | 70 | 10 | 11 | 40 | 60 | 80 | 90 | 13 | 30 | 50 | 12 | 20 | 37 | 82 | 81 | 51 | 61 | 71 | 72 | 21 | 22 | 41 | 42 | 33 | 34 | 31 | 32 | 36 | 35 |
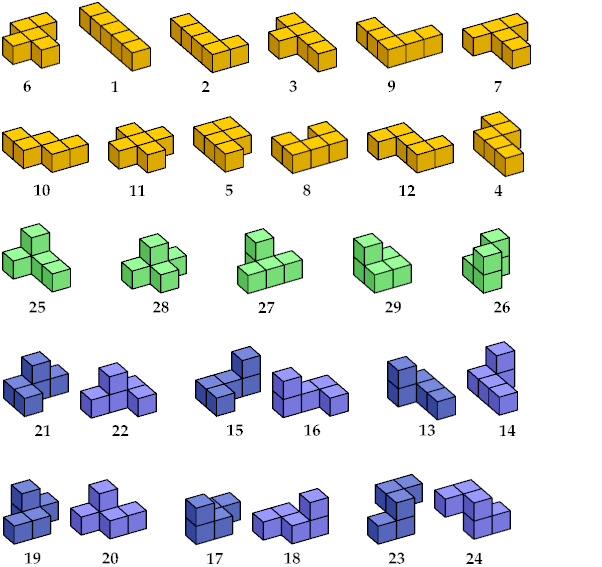
| Abaroth | 6 | 1 | 2 | 4 | 5 | 7 | 8 | 9 | 10 | 11 | 3 | 12 | 26 | 27 | 25 | 28 | 29 | 21 | 22 | 15 | 16 | 13 | 14 | 19 | 20 | 17 | 18 | 23 | 24 |
| Knuth | r | o | q | s | p | t | u | v | w | x | y | z | j | n | l | m | k | b | B | a | A | c | C | e | E | d | D | F | f |
| Sicherman | F | I | L | N | P | T | U | V | W | X | Y | Z | A | B | K | M | Q | E | E′ | S | S′ | J | J′ | R | R′ | H | H′ | G | G′ |
My copy of the book is a gift from Dr. Knuth.
Last revised 2024-01-19.