Two-sided polyrhons may be reflected as well as rotated. One-sided polyrhons may be rotated but not reflected.
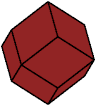
The Puzzling World of Polyhedral Dissections by Stewart T. Coffin describes polyrhons in Chapter 18. You can find the book on line here. See also Torsten Sillke's notes on polyspheres, which are joined like polyrhons but have an additional symmetry. For example, the red trirhon below lacks mirror symmetry; the corresponding trisphere has it. Abaroth's page Polyspheres presents a description and several constructions for polyspheres.
| Order | Two-Sided | One-Sided |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
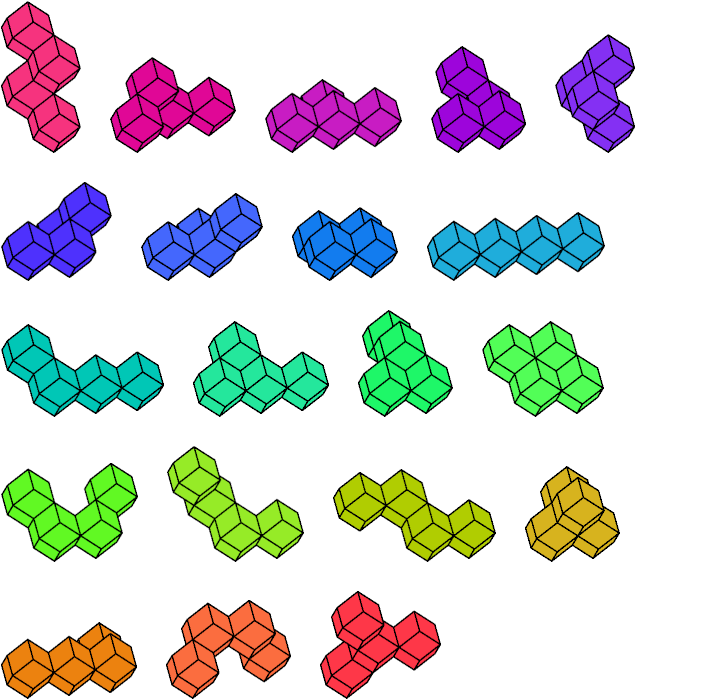
| 3 | 4 | 5 |
| 4 | 20 | 28 |
| 5 | 131 | 225 |
| 6 | 1 211 | 2 274 |
| 7 | 12 734 | 24 955 |
| 8 | 144 158 | 286 143 |
| 9 | 1 687 737 | 3 367 443 |
| 10 | 20 196 788 | 40 358 811 |

Last revised 2014-11-11.