Polyominoids may be generalized to other dimensions. An (n,k)-polyominoid is a set of k-dimensional cells in the n-dimensional grid, connected at (k−1)-dimensional cells. Examples:
| n | k | Name |
|---|---|---|
| 2 | 1 | polyline or polystick |
| 2 | 2 | polyomino |
| 3 | 1 | 3D polystick |
| 3 | 2 | ordinary polyominoid |
| 3 | 3 | polycube |
One can further generalize polyominoids by specifying the dimension of their cell connections. For example, a polyking may be regarded as a (2,2,0)-polyominoid.
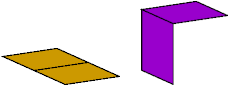
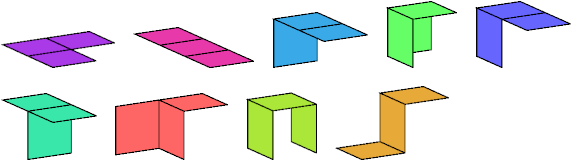
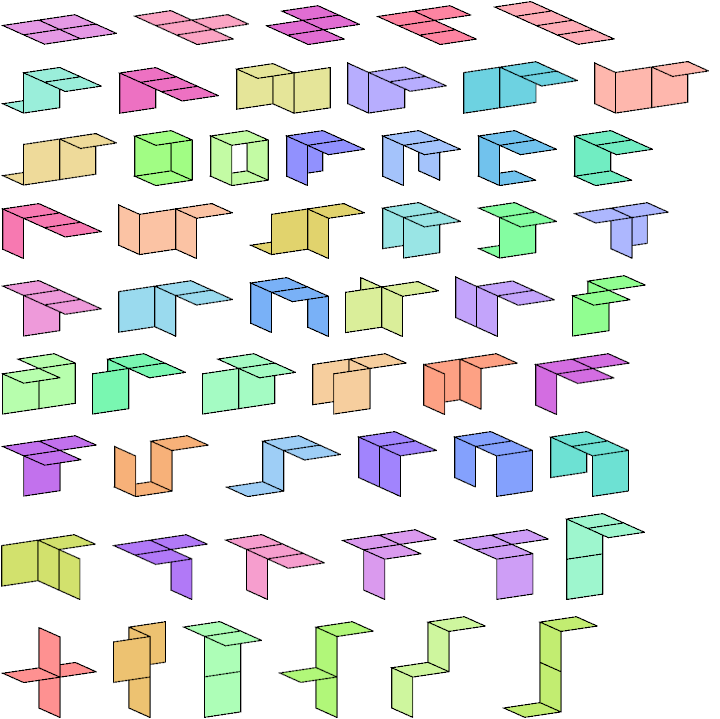
Here I show all (3,2)-polyominoids with at most 4 cells. Like polycubes, polyominoids may be one-sided or two-sided. One-sided means that distinct mirror images are counted as different polyominoids. Two-sided means that distinct mirror images are counted as the same polyominoid.
| Cells | Two-Sided A075679 | One-Sided A056846 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 9 | 11 |
| 4 | 54 | 80 |
| 5 | 448 | 780 |
| 6 | 4650 | 8781 |
| 7 | 53611 | 104828 |
The diagrams below show the two-sided polyominoids.

Last revised 2022-05-31.