Catalogue of Tetrakis Polyaboloes

A polyabolo is a figure made of equal isosceles right triangles joined at equal edges. The tetrakis grid is a square grid whose cells are subdivided into diagonal halves, using alternate diagonals. A tetrakis polyabolo is a polyabolo whose cells conform to the tetrakis grid. It is equivalent to a polyform whose cells are triangular quadrants of the cells in a square grid. In particular, every polyomino is a tetrakis polyabolo.

Thanks to Mark Smith for drawing my attention to tetrakis polyaboloes.

Enumeration

Two-sided tetrakis polyaboloes may be rotated and reflected. One-sided tetrakis polyaboloes may be rotated but not reflected.

Thanks to Joseph S. Myers for clearing up a point about enumerating tetrakis polyaboloes.

Order Two-Sided One-Sided

1 1 1

2 2 2

3 2 3

4 6 8

5 8 14

6 21 34

7 42 80

8 110 202

9 252 494

10 642 1 242

11 1 584 3 144

12 4 066 8 035

13 10 369 20 676

14 26 842 53 439

15 69 651 139 144

16 181 784 362 963

17 476 272 952 148

18 1 251 826 2 502 128

19 3 302 187 6 603 367

20 8 729 026 17 454 225

Order	Two-Sided	One-Sided
1	1	1
2	2	2
3	2	3
4	6	8
5	8	14
6	21	34
7	42	80
8	110	202
9	252	494
10	642	1 242
11	1 584	3 144
12	4 066	8 035
13	10 369	20 676
14	26 842	53 439
15	69 651	139 144
16	181 784	362 963
17	476 272	952 148
18	1 251 826	2 502 128
19	3 302 187	6 603 367
20	8 729 026	17 454 225

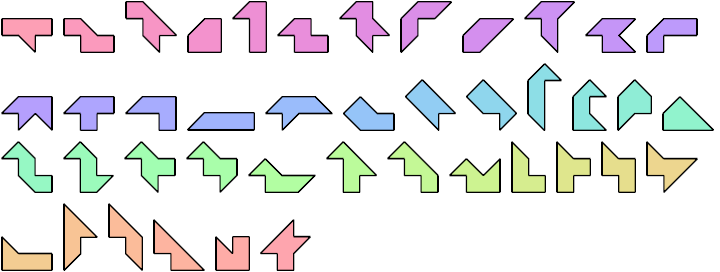
The figures below show two-sided tetrakis polyaboloes.

Monabolo

Diaboloes

Triaboloes

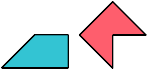
Tetraboloes

Pentaboloes

Hexaboloes

Heptaboloes

Back to Polyform Catalogues < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]