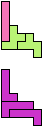
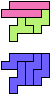

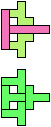
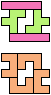


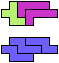



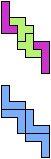




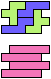
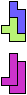
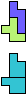
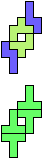
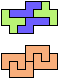
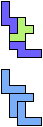
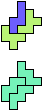

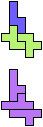
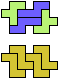


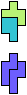





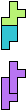





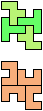
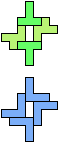






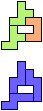

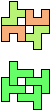
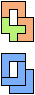

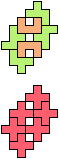
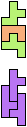



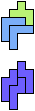
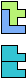
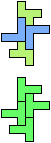
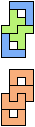
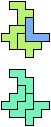
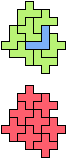
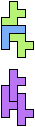

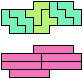



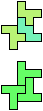
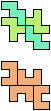
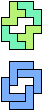




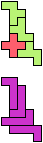
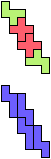


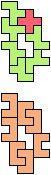
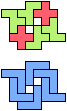
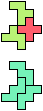



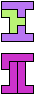

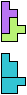

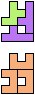
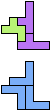



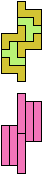




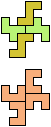
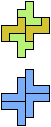
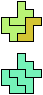


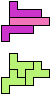


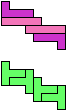

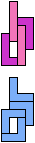

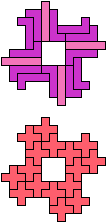
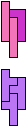

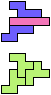



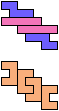
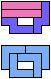

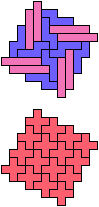
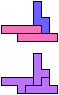
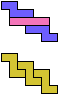



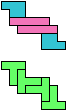
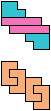
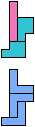
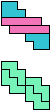

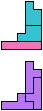

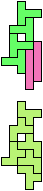



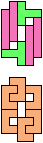

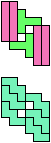
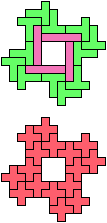

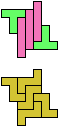


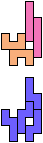
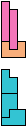

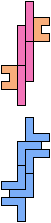

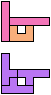

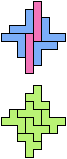



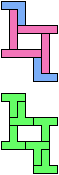

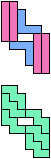

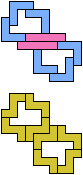



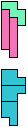
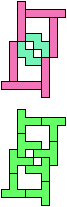
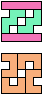
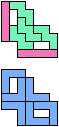
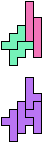
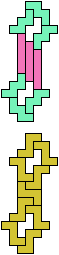

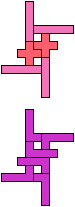
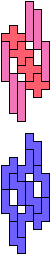
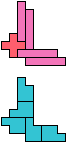

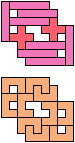

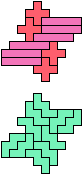

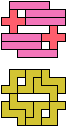
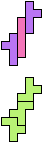
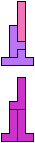

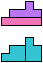

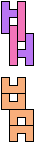

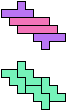


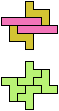

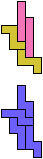
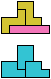

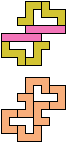
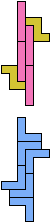
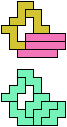
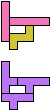





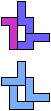

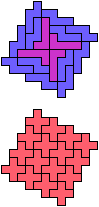

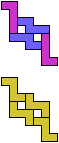


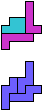


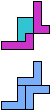









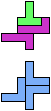
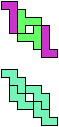
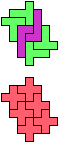
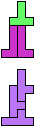

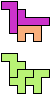

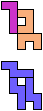


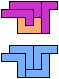


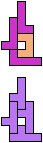

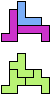
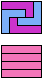
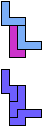


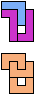
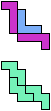
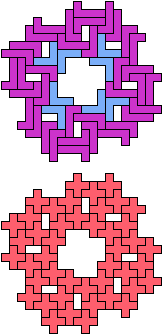
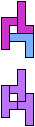





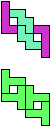

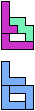
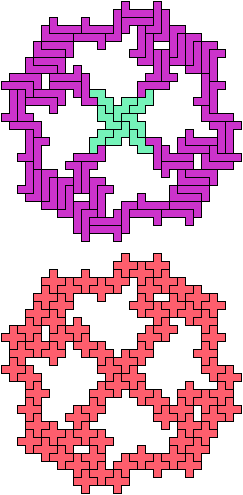
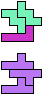

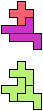
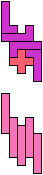


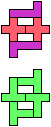
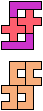
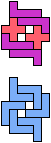
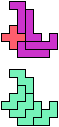
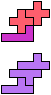


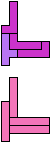


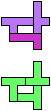

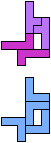



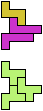





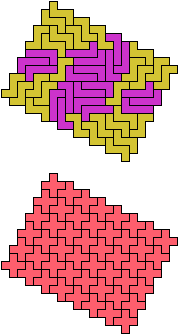
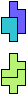
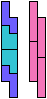



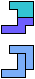

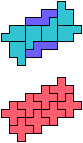


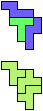


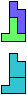
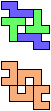
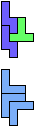
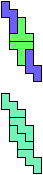
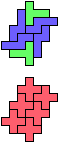





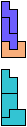
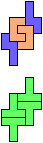
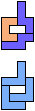
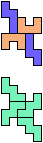
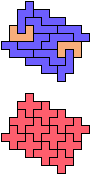


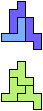


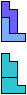
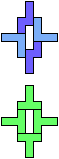

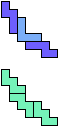
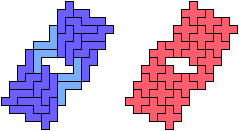


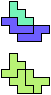
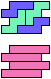
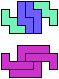
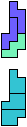

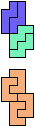
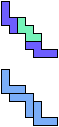

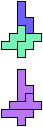
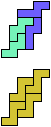




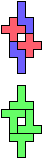
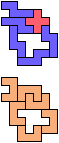
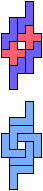
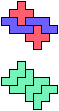
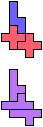


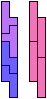
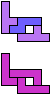

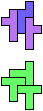
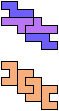
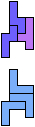



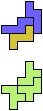


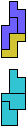
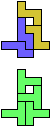
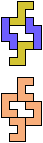
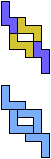
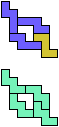
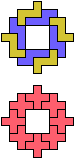



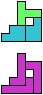

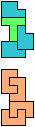
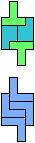
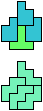

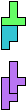

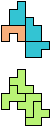
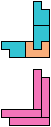

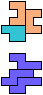

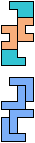
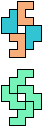
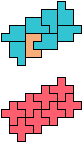

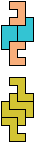


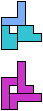
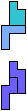



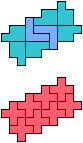





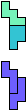

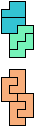
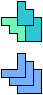
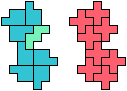
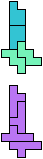
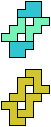





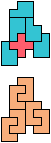
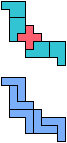


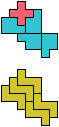






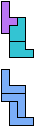
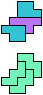











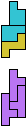
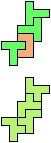
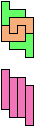
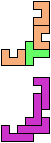
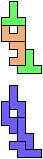
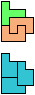
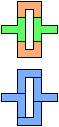
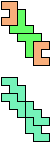
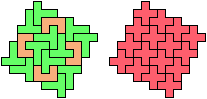
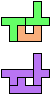
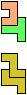
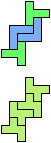
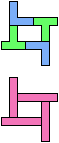
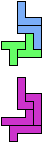
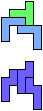

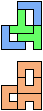
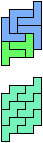
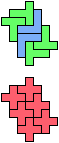







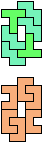
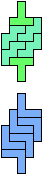
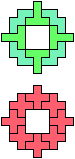


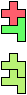
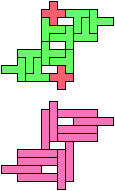
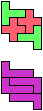
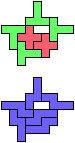
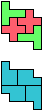
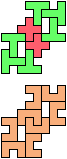
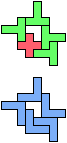
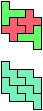



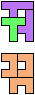
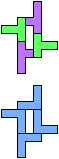
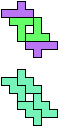



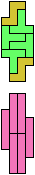

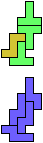
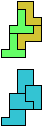
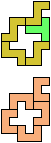
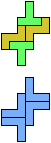
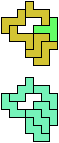
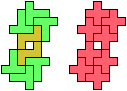

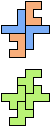

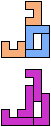
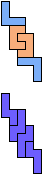
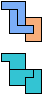
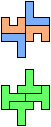


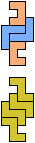
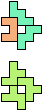
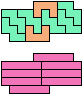
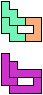
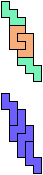

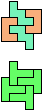
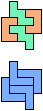
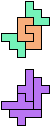
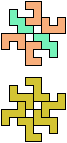

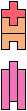


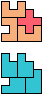


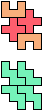
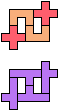

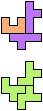


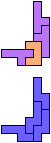
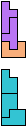
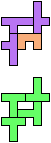
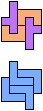
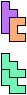


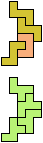
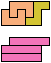

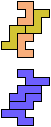

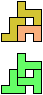
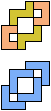
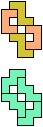
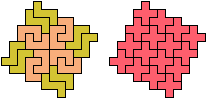
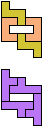


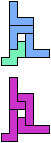

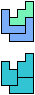
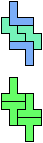
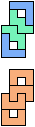
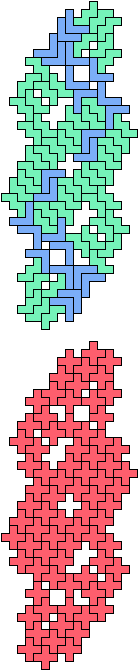
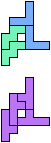
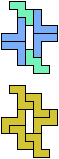

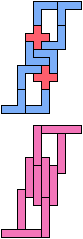
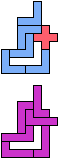
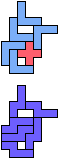

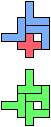
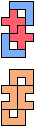
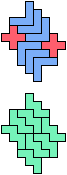
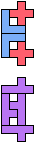



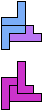
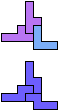
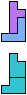
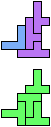
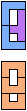


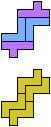


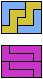
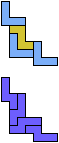
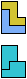
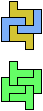
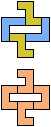
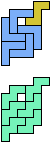
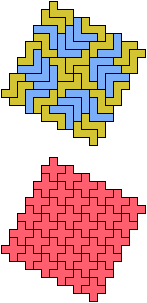
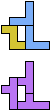
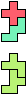
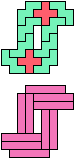



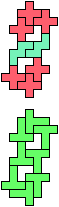
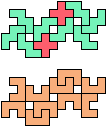
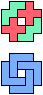
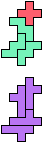




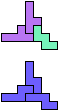
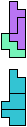
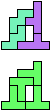
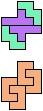

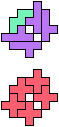


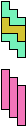

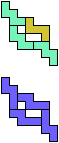



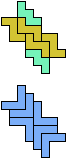







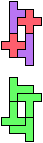
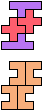
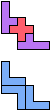


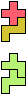
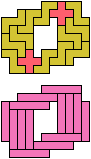




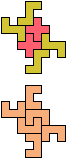
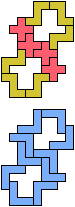

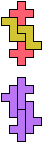
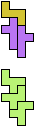
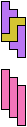





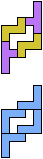
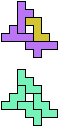

The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Polyomino compatibility has been widely studied since 1992, when Pablo Coll first posed and studied the problem for pentominoes.
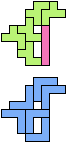
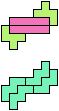
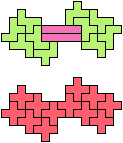
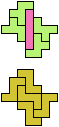
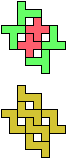
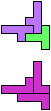
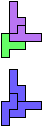
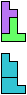
Here I show minimal known compatibilities for a single pentomino and a pair of other pentominoes, using at least one copy of each pentomino of the pair.
| F+I | L: 3 | N: 4 | P: 3 | T: 4 | U: 4 | V: 6 | W: 4 | X: 12 | Y: 3 | Z: 5 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  |  | |||
| F+L | I: 4 | N: 3 | P: 3 | T: 4 | U: 3 | V: 4 | W: 3 | X: 4 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+N | I: 4 | L: 2 | P: 2 | T: 4 | U: 4 | V: 3 | W: 3 | X: 4 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+P | I: 4 | L: 2 | N: 2 | T: 3 | U: 4 | V: 3 | W: 2 | X: 5 | Y: 2 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+T | I: 6 | L: 3 | N: 3 | P: 2 | U: 4 | V: 4 | W: 3 | X: 3 | Y: 2 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+U | I: 6 | L: 3 | N: 3 | P: 3 | T: 4 | V: 3 | W: 3 | X: 6 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+V | I: 4 | L: 4 | N: 3 | P: 2 | T: 4 | U: 4 | W: 4 | X: 8 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+W | I: 6 | L: 3 | N: 3 | P: 3 | T: 3 | U: 4 | V: 4 | X: 3 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+X | I: 10 | L: 4 | N: 4 | P: 4 | T: 3 | U: 7 | V: 6 | W: 3 | Y: 2 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+Y | I: 3 | L: 3 | N: 3 | P: 2 | T: 3 | U: 3 | V: 3 | W: 3 | X: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| F+Z | I: 6 | L: 3 | N: 4 | P: 3 | T: 3 | U: 4 | V: 4 | W: 3 | X: 3 | Y: 2 | ||
 |  |  |  |  |  |  |  |  |  | |||
| I+L | F: 3 | N: 4 | P: 2 | T: 4 | U: 3 | V: 4 | W: 4 | X: 16 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| I+N | F: 3 | L: 4 | P: 3 | T: 4 | U: 4 | V: 4 | W: 4 | X: 16 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| I+P | F: 4 | L: 3 | N: 3 | T: 4 | U: 4 | V: 3 | W: 4 | X: 6 | Y: 3 | Z: 3 | ||
 |  |  |  | 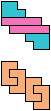 |  |  |  |  |  | |||
| I+T | F: 6 | L: 4 | N: 4 | P: 3 | U: 6 | V: 4 | W: 6 | X: 16 | Y: 3 | Z: 5 | ||
 |  |  |  |  |  |  |  |  |  | |||
| I+U | F: 4 | L: 2 | N: 4 | P: 3 | T: 4 | V: 6 | W: 4 | X: ? | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  | ||||
| I+V | F: 6 | L: 4 | N: 4 | P: 3 | T: 6 | U: 6 | W: 6 | X: ? | Y: 2 | Z: 8 | ||
 |  |  |  |  |  |  |  |  | ||||
| I+W | F: 4 | L: 4 | N: 4 | P: 3 | T: 8 | U: 4 | V: 6 | X: ? | Y: 4 | Z: 9 | ||
 |  |  |  |  |  |  |  |  | ||||
| I+X | F: 6 | L: 6 | N: 10 | P: 5 | T: 10 | U: 10 | V: 12 | W: 10 | Y: 3 | Z: 8 | ||
 |  |  |  |  |  |  |  |  |  | |||
| I+Y | F: 3 | L: 3 | N: 4 | P: 2 | T: 4 | U: 4 | V: 4 | W: 4 | X: 3 | Z: 3 | ||
 |  |  |  |  | 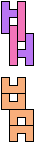 |  |  |  |  | |||
| I+Z | F: 4 | L: 2 | N: 4 | P: 3 | T: 4 | U: 6 | V: 6 | W: 6 | X: ? | Y: 3 | ||
 |  |  |  |  |  | 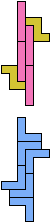 |  |  | ||||
| L+N | F: 2 | I: 4 | P: 2 | T: 3 | U: 4 | V: 3 | W: 4 | X: 16 | Y: 2 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| L+P | F: 3 | I: 3 | N: 3 | T: 4 | U: 3 | V: 3 | W: 3 | X: 6 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| L+T | F: 3 | I: 4 | N: 2 | P: 3 | U: 3 | V: 3 | W: 4 | X: 6 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| L+U | F: 3 | I: 3 | N: 3 | P: 2 | T: 3 | V: 4 | W: 4 | X: 96 | Y: 4 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| L+V | F: 3 | I: 4 | N: 3 | P: 3 | T: 3 | U: 3 | W: 3 | X: 44 | Y: 3 | Z: 4 | ||
 |  |  |  |  | 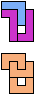 |  |  |  |  | |||
| L+W | F: 3 | I: 4 | N: 4 | P: 3 | T: 4 | U: 4 | V: 3 | X: 80 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| L+X | F: 3 | I: 5 | N: 4 | P: 4 | T: 4 | U: 4 | V: 6 | W: 5 | Y: 3 | Z: 7 | ||
 |  |  |  | 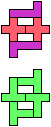 | 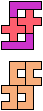 |  |  |  |  | |||
| L+Y | F: 2 | I: 4 | N: 3 | P: 2 | T: 3 | U: 2 | V: 4 | W: 4 | X: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| L+Z | F: 3 | I: 3 | N: 4 | P: 3 | T: 3 | U: 3 | V: 4 | W: 4 | X: 48 | Y: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+P | F: 2 | I: 4 | L: 2 | T: 3 | U: 4 | V: 2 | W: 3 | X: 8 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+T | F: 3 | I: 4 | L: 3 | P: 2 | U: 4 | V: 3 | W: 4 | X: 6 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+U | F: 4 | I: 4 | L: 3 | P: 3 | T: 4 | V: 3 | W: 4 | X: 12 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+V | F: 3 | I: 4 | L: 3 | P: 2 | T: 4 | U: 4 | W: 3 | X: 20 | Y: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+W | F: 3 | I: 4 | L: 4 | P: 3 | T: 4 | U: 4 | V: 3 | X: 8 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+X | F: 3 | I: 6 | L: 6 | P: 4 | T: 4 | U: 6 | V: 6 | W: 4 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+Y | F: 2 | I: 4 | L: 3 | P: 2 | T: 3 | U: 4 | V: 3 | W: 4 | X: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| N+Z | F: 3 | I: 3 | L: 4 | P: 3 | T: 4 | U: 4 | V: 4 | W: 4 | X: 8 | Y: 3 | ||
 |  |  |  |  | 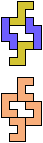 |  |  |  |  | |||
| P+T | F: 3 | I: 3 | L: 3 | N: 3 | U: 4 | V: 4 | W: 4 | X: 6 | Y: 2 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| P+U | F: 4 | I: 4 | L: 3 | N: 3 | T: 4 | V: 4 | W: 4 | X: 8 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  | 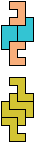 | |||
| P+V | F: 3 | I: 3 | L: 3 | N: 2 | T: 4 | U: 3 | W: 4 | X: 8 | Y: 3 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| P+W | F: 3 | I: 4 | L: 2 | N: 2 | T: 4 | U: 4 | V: 3 | X: 8 | Y: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| P+X | F: 3 | I: 5 | L: 3 | N: 4 | T: 5 | U: 6 | V: 5 | W: 4 | Y: 3 | Z: 5 | ||
 |  |  |  |  |  |  |  |  |  | |||
| P+Y | F: 2 | I: 3 | L: 2 | N: 3 | T: 2 | U: 3 | V: 3 | W: 3 | X: 4 | Z: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| P+Z | F: 3 | I: 3 | L: 3 | N: 3 | T: 3 | U: 4 | V: 4 | W: 3 | X: 6 | Y: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| T+U | F: 4 | I: 4 | L: 4 | N: 4 | P: 3 | V: 4 | W: 4 | X: 16 | Y: 3 | Z: 2 | ||
 |  |  |  |  |  |  |  |  |  | |||
| T+V | F: 4 | I: 4 | L: 4 | N: 3 | P: 2 | U: 4 | W: 6 | X: 6 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| T+W | F: 2 | I: 4 | L: 4 | N: 3 | P: 3 | U: 6 | V: 6 | X: 8 | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| T+X | F: 2 | I: 12 | L: 4 | N: 6 | P: 4 | U: 8 | V: 5 | W: 4 | Y: 4 | Z: 6 | ||
 |  |  |  |  |  |  |  |  |  | |||
| T+Y | F: 3 | I: 4 | L: 3 | N: 3 | P: 2 | U: 3 | V: 4 | W: 4 | X: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| T+Z | F: 2 | I: 6 | L: 4 | N: 4 | P: 4 | U: 5 | V: 4 | W: 6 | X: 8 | Y: 3 | ||
 | 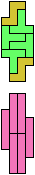 |  |  |  |  |  |  |  |  | |||
| U+V | F: 4 | I: 4 | L: 4 | N: 4 | P: 3 | T: 4 | W: 4 | X: ? | Y: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  | 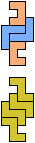 | ||||
| U+W | F: 3 | I: 8 | L: 3 | N: 4 | P: 3 | T: 4 | V: 4 | X: ? | Y: 4 | Z: 6 | ||
 |  |  |  |  |  |  |  |  | ||||
| U+X | F: 4 | I: 3 | L: 4 | N: 4 | P: 4 | T: 6 | V: 4 | W: 4 | Y: 4 | Z: 6 | ||
 |  |  |  |  |  |  |  |  |  | |||
| U+Y | F: 3 | I: 4 | L: 3 | N: 4 | P: 3 | T: 4 | V: 4 | W: 2 | X: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| U+Z | F: 4 | I: 3 | L: 2 | N: 4 | P: 3 | T: 3 | V: 4 | W: 4 | X: 16 | Y: 4 | ||
 |  |  |  |  |  | 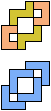 |  |  |  | |||
| V+W | F: 4 | I: 4 | L: 4 | N: 2 | P: 3 | T: 4 | U: 4 | X: 76 | Y: 4 | Z: 6 | ||
 |  |  |  |  |  |  |  |  |  | |||
| V+X | F: 4 | I: 10 | L: 6 | N: 6 | P: 5 | T: 4 | U: 4 | W: 8 | Y: 4 | Z: 6 | ||
 |  |  |  |  |  |  |  |  |  | |||
| V+Y | F: 3 | I: 4 | L: 3 | N: 3 | P: 2 | T: 4 | U: 3 | W: 4 | X: 3 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| V+Z | F: 4 | I: 3 | L: 4 | N: 4 | P: 2 | T: 4 | U: 4 | W: 6 | X: 36 | Y: 3 | ||
 |  |  |  |  |  |  |  |  |  | |||
| W+X | F: 2 | I: 10 | L: 4 | N: 4 | P: 3 | T: 8 | U: 10 | V: 4 | Y: 4 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| W+Y | F: 3 | I: 4 | L: 3 | N: 3 | P: 3 | T: 4 | U: 4 | V: 4 | X: 5 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| W+Z | F: 2 | I: 3 | L: 4 | N: 4 | P: 3 | T: 6 | U: 4 | V: 6 | X: 16 | Y: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| X+Y | F: 3 | I: 3 | L: 4 | N: 4 | P: 4 | T: 4 | U: 4 | V: 3 | W: 5 | Z: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| X+Z | F: 2 | I: 14 | L: 6 | N: 4 | P: 4 | T: 4 | U: 6 | V: 10 | W: 6 | Y: 4 | ||
 |  |  |  |  |  |  |  |  |  | |||
| Y+Z | F: 3 | I: 3 | L: 3 | N: 4 | P: 3 | T: 3 | U: 3 | V: 4 | W: 4 | X: 4 | ||
 |  |  |  |  |  |  |  |  |  |
Last revised 2020-12-06.