Pentahex Compatibility

Introduction

A pentahex is a figure made of five regular hexagons joined edge to edge. There are 22 such figures, not distinguishing reflections and rotations.

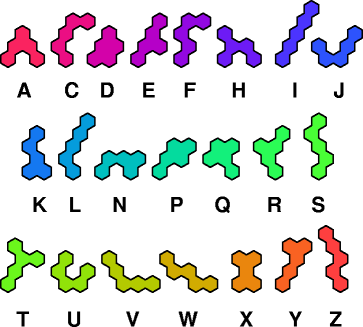
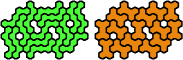
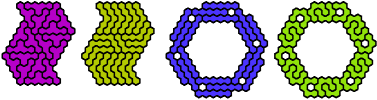
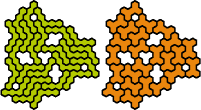
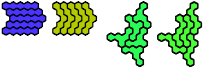
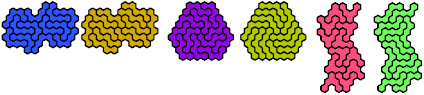
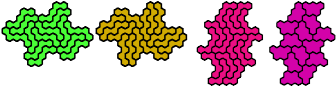
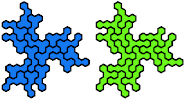
Dr. Erich Friedman's Math Magic for September 2004 shows compatibility figures for pairs of pentahexes (and many other polyforms). Here are minimal known compatibility figures for pairs of pentahexes. Joe DeVincentis and Dr. Friedman found many solutions. Dr. Andrejs Cibulis was the first to solve some of the hardest compatibilities.

For compatible pairs of pentahexes with an odd number of tiles, see Pentahex Odd Pairs.

A convenient set of acrylic pentahexes (and smaller polyhexes) is available from Kadon Enterprises as Hexnut.

  • Nomenclature
  • Minimal Solutions
  • Holeless Variants
  • Vertically Symmetric Variants

    • Nomenclature

    I adopt Dr. Friedman's nomenclature:

    Minimal Solutions

     ACDEFHIJKLNPQRSTUVWXYZ
    A*422223222223266628323
    C4*332392222222223233032
    D23*3332222222226232322
    E233*3224222222233182222
    F2233*29222223222262662
    H23322*102222223223112362
    I3922910*38232835?18353522
    J2224223*22222223223322
    K22222282*2222222332222
    L222222222*222222222823
    N2222223222*23233222322
    P22222222222*2236222222
    Q322232822232*222642222
    R2222233222222*22324222
    S62222252223322*22341522
    T626322?32236222*3266022
    U63232318232226323*627862
    V2231861132322242326*102422
    W8322225322222446210*662
    X3303263353283222156078246*24
    Y23226622222222226262*2
    Z322222222322222222242*

    2 Tiles

    3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    11 Tiles

    15 Tiles

    18 Tiles

    24 Tiles

    30 Tiles

    35 Tiles

    60 Tiles

    78 Tiles

     

    Holeless Variants

    In the table, green figures indicate solutions that are minimal even without the condition of holelessness. Below I show only holeless solutions that differ from those shown above.

     ACDEFHIJKLNPQRSTUVWXYZ
    A*?22229222223212??68324
    C?*14102910232239222363?103
    D214*333222222222?232322
    E2103*32282322228??182222
    F2233*31023222323?2122682
    H29323*102222223823162362
    I910221010*610232885??55?22
    J2228226*222223232212322
    K232232102*22222215332222
    L222322222*222222422823
    N2222223222*233322242322
    P23222222222*223?222222
    Q392232822232*222642224
    R2222238322322*52326422
    S122283852223325*?231411522
    T?2???2?315222?22?*32??2?
    U?32?23?234226323*10??62
    V663181216523242423210*10?22
    W83222251222222614??10*662
    X3?3263?3283224115???6*24
    Y210228622222222226262*2
    Z432222222322422?22242*

    3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    12 Tiles

    14 Tiles

    15 Tiles

    16 Tiles

    22 Tiles

    115 Tiles

     

    Last revised 2023-05-07.

    Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]