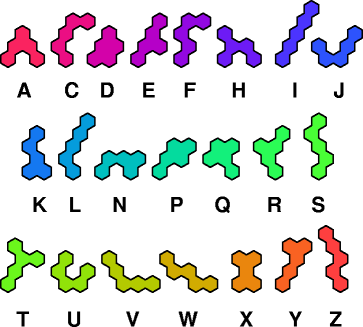
A set of polyforms is compatible if there is a polyform that can be tiled by each member of the set.
In Pentahex Compatibility
I show minimal known compatibilities for every pair of pentahexes.
Here I show minimal known compatibilities that have vertical mirror symmetry.
(Vertical
is relative to the orientation of the pentahex cells.
Some researchers turn the cells 90°.
With this orientation, the symmetry would be horizontal.)
If you find a smaller solution or solve an unsolved case, please write.

| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | ? | 24 | 12 | ? | ? | 24 | 6 | 21 | 21 | 6 | 12 | 6 | 6 | ? | ? | 6 | 24 | ? | 12 | 12 | 54 |
| C | ? | * | 4 | ? | ? | ? | ? | 2 | 36 | 4 | 6 | 6 | 6 | 6 | ? | ? | ? | 2 | ? | ? | ? | ? |
| D | 24 | 4 | * | 18 | 6 | 30 | 12 | 3 | 3 | 4 | 2 | 2 | 6 | 4 | 12 | ? | 2 | 6 | 4 | 48 | 4 | 6 |
| E | 12 | ? | 18 | * | 18 | 12 | 18 | 60 | 12 | 18 | 6 | 12 | 12 | 18 | 60 | ? | ? | 18 | 12 | 6 | 12 | 44 |
| F | ? | ? | 6 | 18 | * | 6 | 18 | 30 | 30 | 6 | 12 | 6 | 6 | 6 | ? | ? | 2 | 6 | 2 | 48 | 18 | 36 |
| H | ? | ? | 30 | 12 | 6 | * | 30 | 6 | 6 | 12 | 6 | 12 | 6 | 12 | 39 | 4 | 6 | ? | 2 | 24 | 18 | 2 |
| I | 24 | ? | 12 | 18 | 18 | 30 | * | 16 | 24 | 6 | 12 | 12 | 60 | 54 | 60 | ? | ? | 6 | 5 | ? | 4 | 4 |
| J | 6 | 2 | 3 | 60 | 30 | 6 | 16 | * | 3 | 2 | 3 | 3 | 6 | 6 | 6 | 18 | 2 | 2 | ? | ? | 12 | 9 |
| K | 21 | 36 | 3 | 12 | 30 | 6 | 24 | 3 | * | 12 | 6 | 3 | 12 | 6 | 18 | 2 | 36 | 30 | 6 | 12 | 6 | 6 |
| L | 21 | 4 | 4 | 18 | 6 | 12 | 6 | 2 | 12 | * | 10 | 6 | 24 | 6 | 24 | 6 | 2 | 6 | 6 | 42 | 10 | 6 |
| N | 6 | 6 | 2 | 6 | 12 | 6 | 12 | 3 | 6 | 10 | * | 2 | 6 | 6 | 36 | 6 | 2 | 6 | 6 | 6 | 10 | 6 |
| P | 12 | 6 | 2 | 12 | 6 | 12 | 12 | 3 | 3 | 6 | 2 | * | 6 | 6 | 12 | ? | 2 | 6 | 6 | 6 | 10 | 6 |
| Q | 6 | 6 | 6 | 12 | 6 | 6 | 60 | 6 | 12 | 24 | 6 | 6 | * | 6 | 6 | 12 | 36 | 36 | 12 | 12 | 12 | 12 |
| R | 6 | 6 | 4 | 18 | 6 | 12 | 54 | 6 | 6 | 6 | 6 | 6 | 6 | * | 6 | 18 | 6 | 6 | 18 | 2 | 2 | 24 |
| S | ? | ? | 12 | 60 | ? | 39 | 60 | 6 | 18 | 24 | 36 | 12 | 6 | 6 | * | 3 | 36 | 6 | ? | 30 | 12 | 12 |
| T | ? | ? | ? | ? | ? | 4 | ? | 18 | 2 | 6 | 6 | ? | 12 | 18 | 3 | * | 18 | 6 | ? | ? | ? | 2 |
| U | 6 | ? | 2 | ? | 2 | 6 | ? | 2 | 36 | 2 | 2 | 2 | 36 | 6 | 36 | 18 | * | ? | 2 | ? | 12 | 6 |
| V | 24 | 2 | 6 | 18 | 6 | ? | 6 | 2 | 30 | 6 | 6 | 6 | 36 | 6 | 6 | 6 | ? | * | 30 | ? | 9 | 6 |
| W | ? | ? | 4 | 12 | 2 | 2 | 5 | ? | 6 | 6 | 6 | 6 | 12 | 18 | ? | ? | 2 | 30 | * | 12 | 30 | 6 |
| X | 12 | ? | 48 | 6 | 48 | 24 | ? | ? | 12 | 42 | 6 | 6 | 12 | 2 | 30 | ? | ? | ? | 12 | * | 2 | 24 |
| Y | 12 | ? | 4 | 12 | 18 | 18 | 4 | 12 | 6 | 10 | 10 | 10 | 12 | 2 | 12 | ? | 12 | 9 | 30 | 2 | * | 4 |
| Z | 54 | ? | 6 | 44 | 36 | 2 | 4 | 9 | 6 | 6 | 6 | 6 | 12 | 24 | 12 | 2 | 6 | 6 | 6 | 24 | 4 | * |




















Last revised 2023-01-06.