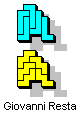Holeless Pentomino Odd Pairs

Introduction

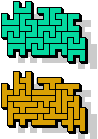
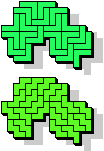
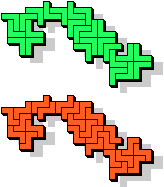
Livio Zucca's Pentomino Odd Pairs studies the problem of finding a compatibility figure for two pentominoes with an odd number of tiles. Here I show holeless variants for pentomino odd pairs. The green cells represent holeless solutions that already appear on Pentomino Odd Pairs.

F I L N P T U V W X Y Z

F * 13 3 5 3 7 9 9 5 19 3 7

I 13 * 9 11 5 ? ? 19 25 × 9 ?

L 3 9 * 5 3 9 11 5 5 ? 3 7

N 5 11 5 * 3 7 7 3 5 33 3 9

P 3 5 3 3 * 3 7 3 3 11 3 3

T 7 ? 9 7 3 * ? ? 67 ? 5 ?

U 9 ? 11 7 7 ? * ? 19 × 19 ?

V 9 19 5 3 3 ? ? * 21 × 7 25

W 5 25 5 5 3 67 19 21 * × 7 15

X 19 × ? 33 11 ? × × × * 25 ×

Y 3 9 3 3 3 5 19 7 7 25 * 7

Z 7 ? 7 9 3 ? ? 25 15 × 7 *

	F	I	L	N	P	T	U	V	W	X	Y	Z
F	*	13	3	5	3	7	9	9	5	19	3	7
I	13	*	9	11	5	?	?	19	25	×	9	?
L	3	9	*	5	3	9	11	5	5	?	3	7
N	5	11	5	*	3	7	7	3	5	33	3	9
P	3	5	3	3	*	3	7	3	3	11	3	3
T	7	?	9	7	3	*	?	?	67	?	5	?
U	9	?	11	7	7	?	*	?	19	×	19	?
V	9	19	5	3	3	?	?	*	21	×	7	25
W	5	25	5	5	3	67	19	21	*	×	7	15
X	19	×	?	33	11	?	×	×	×	*	25	×
Y	3	9	3	3	3	5	19	7	7	25	*	7
Z	7	?	7	9	3	?	?	25	15	×	7	*

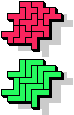
5F+5I	5F+5L	5F+5N	5F+5P	5F+5T	5F+5U

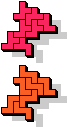
5F+5V	5F+5W	5F+5X	5F+5Y	5F+5Z	5I+5L

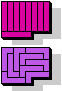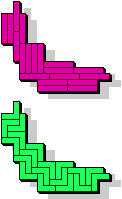
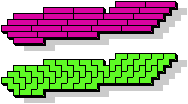
5I+5N	5I+5P	5I+5T	5I+5U	5I+5V	5I+5W

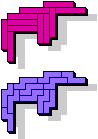
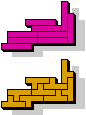
5I+5X	5I+5Y	5I+5Z	5L+5N	5L+5P	5L+5T

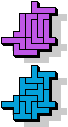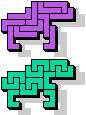
5L+5U	5L+5V	5L+5W	5L+5X	5L+5Y	5L+5Z

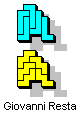
5N+5P	5N+5T	5N+5U	5N+5V	5N+5W	5N+5X

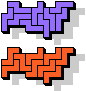
5N+5Y	5N+5Z	5P+5T	5P+5U	5P+5V	5P+5W

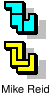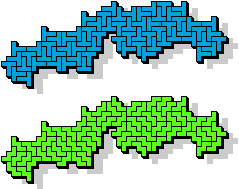
5P+5X	5P+5Y	5P+5Z	5T+5U	5T+5V	5T+5W

5T+5X	5T+5Y	5T+5Z	5U+5V	5U+5W	5U+5X

5U+5Y	5U+5Z	5V+5W	5V+5X	5V+5Y	5V+5Z

5W+5X	5W+5Y	5W+5Z	5X+5Y	5X+5Z	5Y+5Z

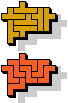Last revised 2022-04-07.

Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]

	F	I	L	N	P	T	U	V	W	X	Y	Z
F	*	13	3	5	3	7	9	9	5	19	3	7
I	13	*	9	11	5	?	?	19	25	×	9	?
L	3	9	*	5	3	9	11	5	5	?	3	7
N	5	11	5	*	3	7	7	3	5	33	3	9
P	3	5	3	3	*	3	7	3	3	11	3	3
T	7	?	9	7	3	*	?	?	67	?	5	?
U	9	?	11	7	7	?	*	?	19	×	19	?
V	9	19	5	3	3	?	?	*	21	×	7	25
W	5	25	5	5	3	67	19	21	*	×	7	15
X	19	×	?	33	11	?	×	×	×	*	25	×
Y	3	9	3	3	3	5	19	7	7	25	*	7
Z	7	?	7	9	3	?	?	25	15	×	7	*

	F	I	L	N	P	T	U	V	W	X	Y	Z
F	*	13	3	5	3	7	9	9	5	19	3	7
I	13	*	9	11	5	?	?	19	25	×	9	?
L	3	9	*	5	3	9	11	5	5	?	3	7
N	5	11	5	*	3	7	7	3	5	33	3	9
P	3	5	3	3	*	3	7	3	3	11	3	3
T	7	?	9	7	3	*	?	?	67	?	5	?
U	9	?	11	7	7	?	*	?	19	×	19	?
V	9	19	5	3	3	?	?	*	21	×	7	25
W	5	25	5	5	3	67	19	21	*	×	7	15
X	19	×	?	33	11	?	×	×	×	*	25	×
Y	3	9	3	3	3	5	19	7	7	25	*	7
Z	7	?	7	9	3	?	?	25	15	×	7	*

	F	I	L	N	P	T	U	V	W	X	Y	Z
F	*	13	3	5	3	7	9	9	5	19	3	7
I	13	*	9	11	5	?	?	19	25	×	9	?
L	3	9	*	5	3	9	11	5	5	?	3	7
N	5	11	5	*	3	7	7	3	5	33	3	9
P	3	5	3	3	*	3	7	3	3	11	3	3
T	7	?	9	7	3	*	?	?	67	?	5	?
U	9	?	11	7	7	?	*	?	19	×	19	?
V	9	19	5	3	3	?	?	*	21	×	7	25
W	5	25	5	5	3	67	19	21	*	×	7	15
X	19	×	?	33	11	?	×	×	×	*	25	×
Y	3	9	3	3	3	5	19	7	7	25	*	7
Z	7	?	7	9	3	?	?	25	15	×	7	*