Trigem Compatibility

A trigem is a plane polyform whose three cells are gems—figures formed by dividing a regular hexagon into thirds using lines from the center to the midpoints of the sides. A gem is one of the two dikites. You can see more about polygems at Abaroth's Polygem Page.

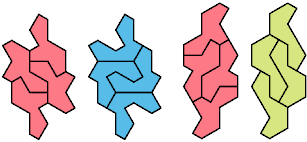
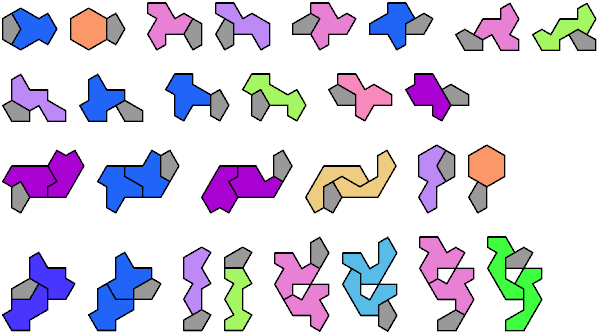
Two or more polyforms are compatible if there is a polyform that each can tile. Here are the minimal known compatibilities for trigems. Most were found by Abaroth. Please write if you find a smaller solution or solve an unsolved case.

  • The Trigems
  • Table of Results
  • 2 Tiles
  • 3 Tiles
  • 4 Tiles
  • 6 Tiles
  • Reëntrant Solutions

    • The Trigems

    Table of Results

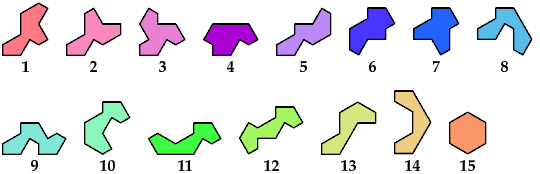
     123456789101112131415
    1*232226433634?3
    22*?R6636626?336
    33?*3R?RR33RR???
    42R3*62R336??3R?
    526R6*3R2336R2?R
    626?23*R??6??3?6
    763RRRR*2666R23R
    846R32?2*366222?
    936333?63*3266??
    10323636663*233?3
    1166R?6?6622*333?
    123?R?R?R2633*???
    1343?32322633?*22
    14?3?R??32??3?2*?
    1536??R6R??3??2?*

    2 Tiles

    3 Tiles

    4 Tiles

    6 Tiles

    Reëntrant Solutions

    Last revised 2020-04-12.

    Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]