Pentacube Compatibility

A pentacube is a solid made of five cubes joined face to face. There are 23 pentacubes, not distinguishing reflections and rotations:

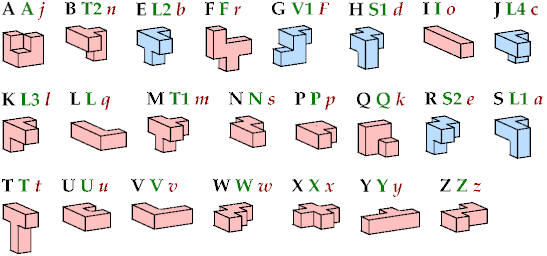
The six blue tiles have left- and right-handed forms. Kate Jones's systematic names are shown in green. The mirror forms of V1, S1–S2, and L1–L4 are called V2, N1–N2, and J1–J4. But L3 and J3 are identical because they have mirror symmetry through a plane diagonal.

Two-Sided Pentacubes

Here are the least known numbers of tiles needed to construct a solid that can be tiled with either of two pentacubes, letting tiles be reflected:

  A B E F G H I J K L M N P Q R S T U V W X Y Z
A*2222282224222224242222
B2*222242422222242224224
E22*22242222222222224222
F222*2252222222222442222
G2222*262224222224232622
H22222*42224222224242622
I844564*38210224864545525
J2222223*224222222224422
K24222282*22222222222822
L222222222*4222222222822
M42224410424*422242664224
N22222222224*222222221022
P222222222222*2222222422
Q2222224222222*224232622
R22222282222222*24242422
S242222622242222*2222622
T4222444222222442*326422
U22242252226222223*22224
V422434422262234222*61424
W2442225422422222626*624
X2222665488210464642146*210
Y222222222222222222222*2
Z24222252224222222444102*
  A B E F G H I J K L M N P Q R S T U V W X Y Z

6 Tiles

8 Tiles

10 Tiles

14 Tiles

One-Sided Pentacubes

Here are the values when tile reflection is not allowed. The blue figures differ from the values where reflection is allowed.

  A B E E′ F G G′ H H′ I J J′ K L M N P Q R R′ S S′ T U V W X Y Z
A*2222332282222422233224242222
B2*222222242242222222442224224
E22*22222242222222233222224222
E′222*2222242222222233222224222
F2222*222252222222222222442222
G32222*222102222422222224442622
G′322222*22102222422222224442622
H2222222*242222422222224242822
H′22222222*42222422222224242822
I84445101044*3382102241010664545525
J2222222223*222422222222224422
J′22222222232*22422222222224422
K242222222822*2222222222222822
L2222222222222*422222222222822
M422224444104424*42222442664224
N222222222222224*22223322221022
P2222222222222222*222222222422
Q22222222242222222*22224232622
R3233222221022222222*2224442422
R′32332222210222222222*224442422
S24222222262222432222*23222622
S′242222222622224322222*3222622
T4222244444222222244433*326422
U22224442252222622244223*22224
V422244444422226223442222*61424
W2444222225442242222222626*624
X2222266885448821046446642146*210
Y222222222222222222222222222*2
Z24222222252222422222222444102*

Last revised 2024-07-06.

Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]