Diabolo-Tetrabolo Compatibility

Introduction

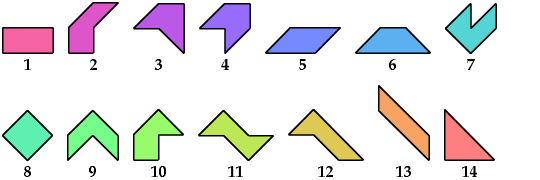
A diabolo is a figure made of two equal isosceles right triangles joined at equal edges. There are 3 such figures, not distinguishing reflections and rotations. A tetrabolo is a figure made of four equal isosceles right triangles joined at equal edges. There are 14 such figures, not distinguishing reflections and rotations.

Here are minimal compatibility figures for diaboloes and tetraboloes. Not all are uniquely minimal.

Summary

Diabolo Numbers

Tetrabolo Numbers

Table

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1 2	×	4 8	×	×	4 8	×	×	×	4 8	×	×	×	2 4
2	×	×	2 4	1 2	1 2	2 4	2 4	×	1 2	4 8	×	2 4	1 2	2 4
3	2 4	4 8	2 4	×	1 2	2 4	2 4	1 2	2 4	4 8	1 2	2 4	2 4	1 2

Solutions

All solutions are minimal. Few are uniquely minimal.

Last revised 2015-04-11.

Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1 2	×	4 8	×	×	4 8	×	×	×	4 8	×	×	×	2 4
2	×	×	2 4	1 2	1 2	2 4	2 4	×	1 2	4 8	×	2 4	1 2	2 4
3	2 4	4 8	2 4	×	1 2	2 4	2 4	1 2	2 4	4 8	1 2	2 4	2 4	1 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1 2	×	4 8	×	×	4 8	×	×	×	4 8	×	×	×	2 4
2	×	×	2 4	1 2	1 2	2 4	2 4	×	1 2	4 8	×	2 4	1 2	2 4
3	2 4	4 8	2 4	×	1 2	2 4	2 4	1 2	2 4	4 8	1 2	2 4	2 4	1 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1 2	×	4 8	×	×	4 8	×	×	×	4 8	×	×	×	2 4
2	×	×	2 4	1 2	1 2	2 4	2 4	×	1 2	4 8	×	2 4	1 2	2 4
3	2 4	4 8	2 4	×	1 2	2 4	2 4	1 2	2 4	4 8	1 2	2 4	2 4	1 2