Holeless Pentomino-Hexomino Compatibility

Introduction

A pentomino is a figure made of five squares joined edge to edge. A hexomino is a figure made of six squares joined edge to edge. There are 12 pentominoes and 35 hexominoes, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Polyomino compatibility has been widely studied since the early 1990s, and two well-known websites, Poly2ominoes by Jorge Mireles and Polypolyominoes by Giovanni Resta, present the results of their authors' systematic searches for compatibility figures. The sites include solutions by other researchers, especially Mike Reid. So far as I know, polyomino compatibility has not been treated in print since Golomb first raised the issue in 1981, except in a series of articles called Polyomino Number Theory, written by Andris Cibulis, Andy Liu, Bob Wainwright, Uldis Barbans, and Gilbert Lee from 2002 to 2005.

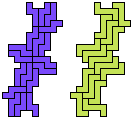
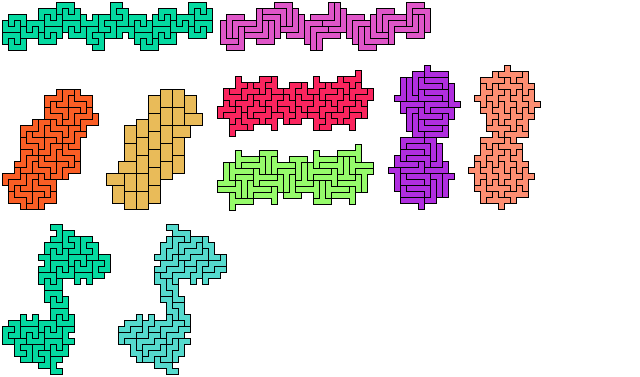
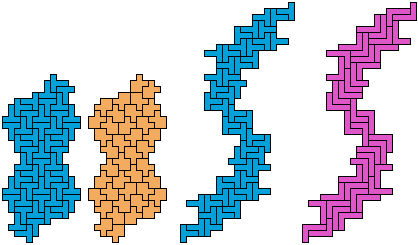
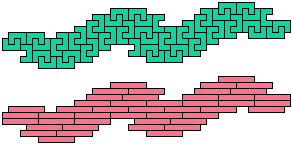
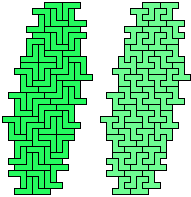
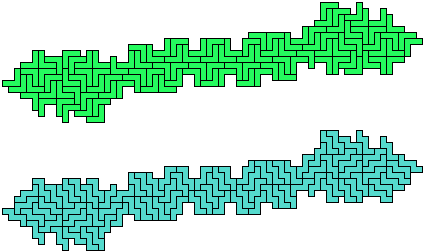
The websites and the articles show only minimal solutions with no restriction. Here I show minimal known pentomino-hexomino compatibility figures without holes. If you find a smaller solution or solve an unsolved case, please let me know.

For pentomino compatibility with or without holes, see Pentomino Compatibility. For hexomino compatibility allowing holes, see Resta's Hexominoes. For hexomino compatibility without holes, see Holeless Hexomino Compatibility.

Pentomino Names

These are Golomb's names for the pentominoes:

Hexomino Numbers

I number the hexominoes from 1 to 35 as shown:

Table

This table shows the smallest number of tiles known to suffice to construct a holeless figure tilable by the pentomino and the hexomino. Green cells indicate solutions that are minimal even if holes are allowed.

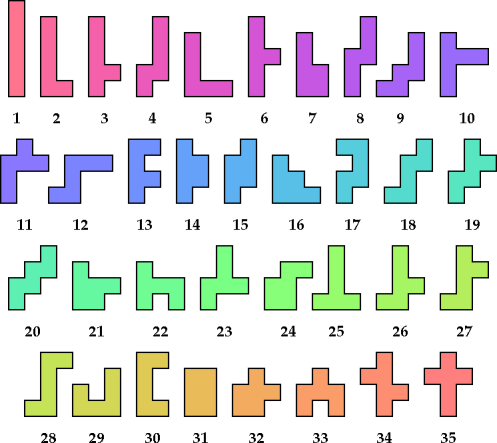
 FILNPTUVWXYZ
15 65 65 610 125 620 2445 545 65 6×5 6?
25 65 65 65 65 610 1210 1210 125 6×5 65 6
35 610 125 65 65 610 1210 1210 1210 12?5 620 24
45 610 125 65 65 6?10 1220 245 6×5 6?
55 65 65 65 65 640 4830 365 65 6×10 1220 24
610 1210 1210 1210 1210 12??10 12?×5 6?
75 65 65 65 65 65 610 125 610 12×5 610 12
85 65 610 125 610 12??5 65 6×5 6?
95 610 125 65 65 620 245 610 125 6×10 1210 12
105 6?5 65 610 125 6?5 6?×5 610 12
115 610 1210 125 65 610 12?5 610 12×10 1220 24
125 610 125 65 65 610 1210 125 65 6120 1445 65 6
135 610 125 610 125 620 245 620 245 610 125 610 12
1410 1210 125 610 125 610 125 610 1210 12×5 6?
155 65 65 65 65 6??10 1210 12×5 6?
1610 1210 125 610 125 6??10 1210 12×10 12?
175 620 245 65 610 12?5 6?10 12×5 6?
185 610 1210 125 65 610 1230 3690 1085 620 245 65 6
195 610 125 65 65 620 2410 1210 125 610 125 610 12
205 65 65 65 65 6??5 65 6×5 65 6
215 610 125 65 65 65 610 1210 125 6?5 610 12
225 610 1210 125 65 65 65 650 6010 12×5 65 6
235 6×10 125 65 65 6?10 1220 24×5 610 12
245 65 65 65 65 620 245 610 125 6?5 65 6
2530 36?5 620 245 65 6?10 12?×??
265 610 125 610 125 65 610 1210 125 610 125 610 12
275 6?5 610 125 6???10 12×5 65 6
2810 12×5 615 185 6???5 6×??
2910 1210 125 65 65 610 125 65 620 24×5 6?
3020 24?5 65 65 6????×5 620 24
3120 245 65 610 125 620 2420 2410 1220 24×10 1230 36
325 6?5 65 65 640 48??5 610 125 65 6
335 65 610 1210 1210 12?10 12?10 12×5 6?
345 6×30 3610 1210 12????×5 610 12
355 6×20 2410 1210 125 6??20 24×5 6?
 FILNPTUVWXYZ

Special Solutions

Here I show only solutions that are larger than the corresponding minimal solutions allowing holes.

So far as I know, these solutions are minimal. They are not necessarily uniquely minimal.

12 Pentominoes, 10 Hexominoes

18 Pentominoes, 15 Hexominoes

24 Pentominoes, 20 Hexominoes

36 Pentominoes, 30 Hexominoes

48 Pentominoes, 40 Hexominoes

54 Pentominoes, 45 Hexominoes

60 Pentominoes, 50 Hexominoes

108 Pentominoes, 90 Hexominoes

144 Pentominoes, 120 Hexominoes

 

Alternate Solutions

Here I show holeless solutions that are no larger than the corresponding solutions allowing holes and do not appear on Resta's page.

 

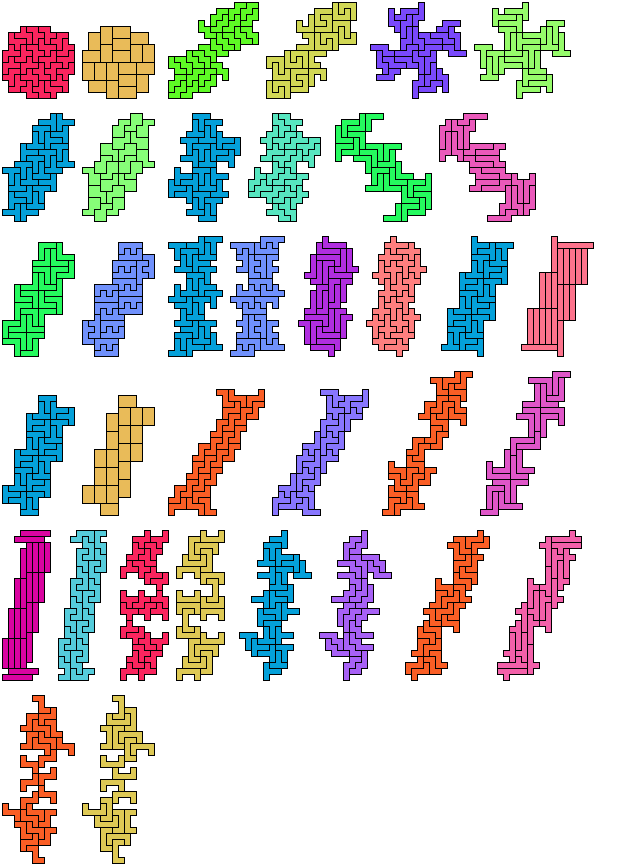
Last revised 2024-02-01.

Back to Pairwise Compatibility < Polyform Compatibility < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]