Polycairo Exclusion

Introduction

In the 1950s, Solomon W. Golomb investigated the question: how few cells can you remove from the plane to exclude the shape of a given polyomino?

Here I investigate the related question: how few cells can you remove from the plane to exclude the shape of a given polycairo? If you find a more efficient exclusion, please write.

Specific Results

Here are some patterns for small polycairos.

To exclude either dicairo you must remove at least 1/2 the cells. This also holds for the two tricairos:

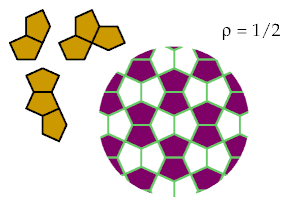
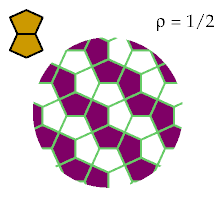
These tricairos are excluded optimally. The tetracairos are probably optimal.

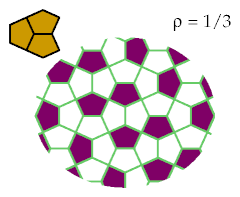
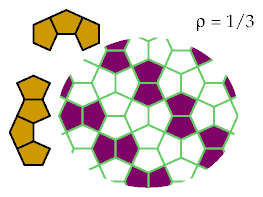
This pattern optimally excludes six tetracairos:

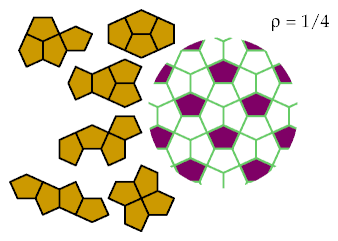
This pattern optimally excludes three tetracairos:

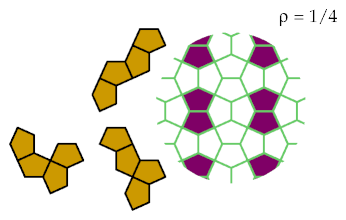
These tetracairos are optimally excluded by these patterns:

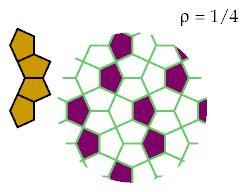
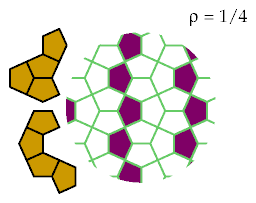
These patterns are the best known for excluding these tetracairos:

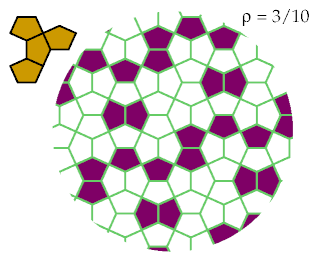
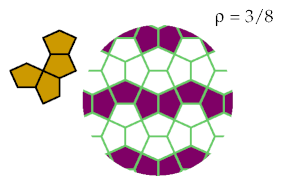
General Results

If a polycairo with n cells tiles the plane, you must remove at least 1/n of the cells, one for each tile.

Optimality Proofs

The next diagram demonstrates the optimality of two of the exclusions with more than 1/n holes. The numbers show how many holes you need in the green figure to exclude the yellow figure:

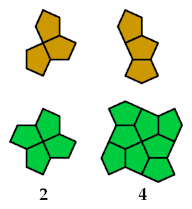
Last revised 2018-05-28.

Back to Polyform Exclusion, Equalization, Variegation, and Integration < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]