2 Tiles
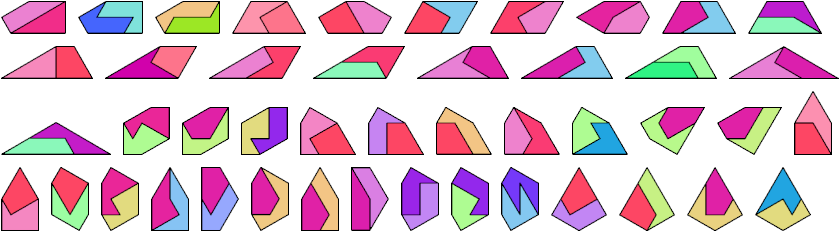
3 Tiles
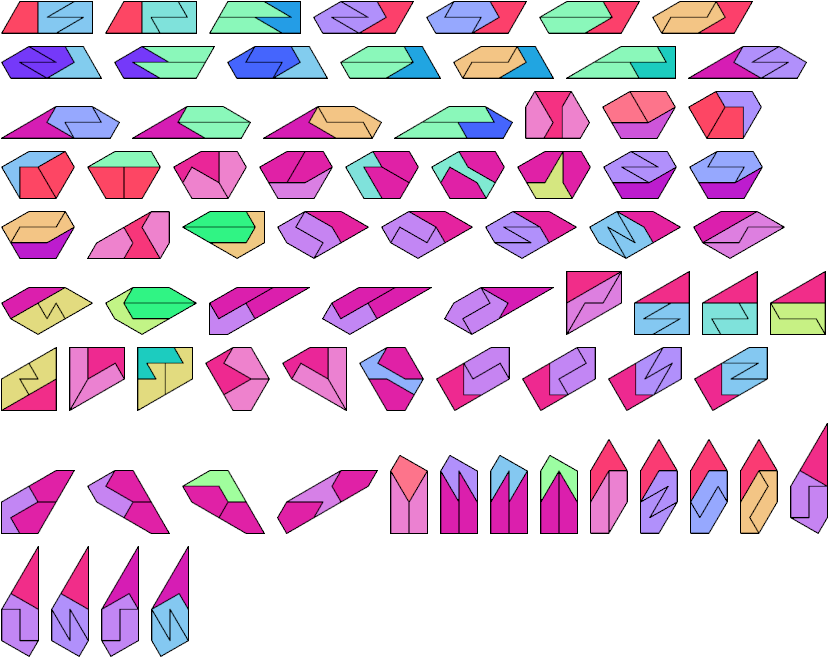
4 Tiles
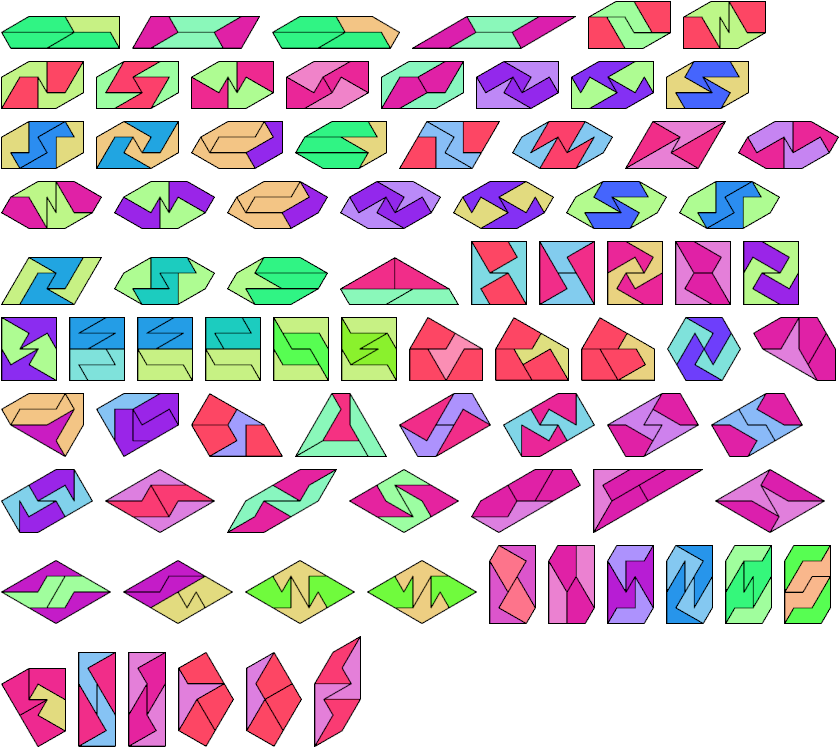
5 Tiles
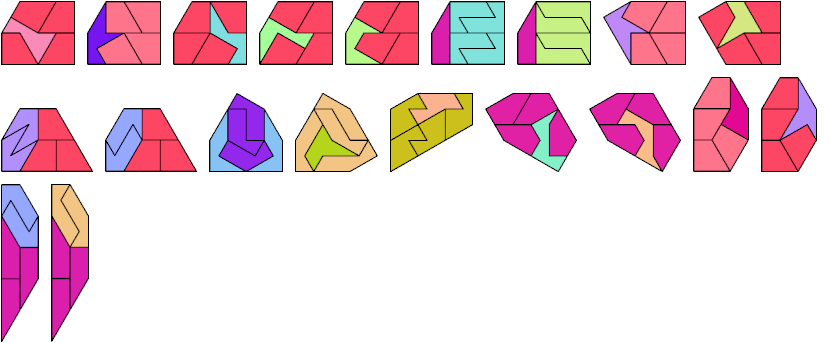
6 Tiles

7 Tiles

8 Tiles

9 Tiles
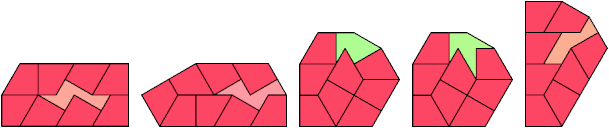
10 Tiles

11 Tiles
12 Tiles

14 Tiles
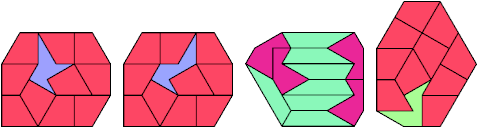
16 Tiles
17 Tiles
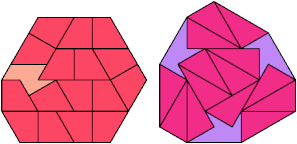
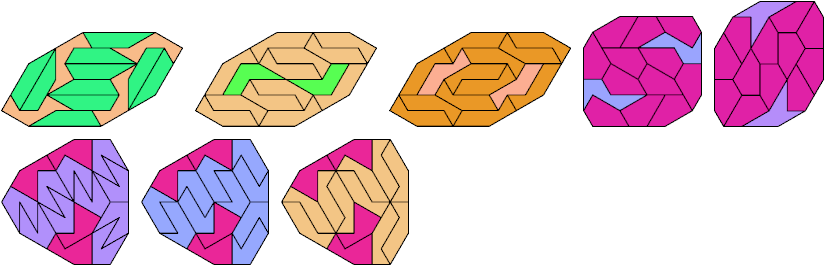
18 Tiles
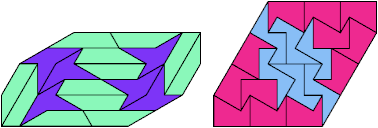
20 Tiles
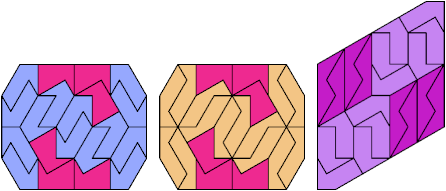
22 Tiles
23 Tiles
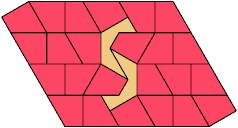
24 Tiles
26 Tiles
29 Tiles
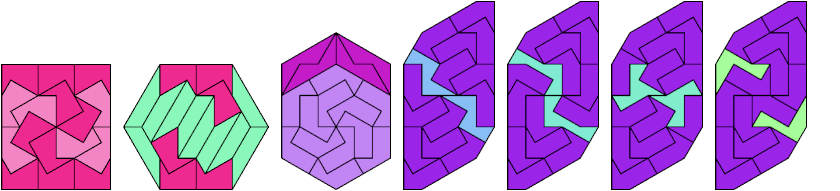
36 Tiles
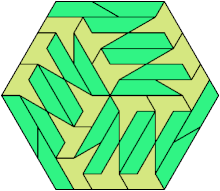
38 Tiles
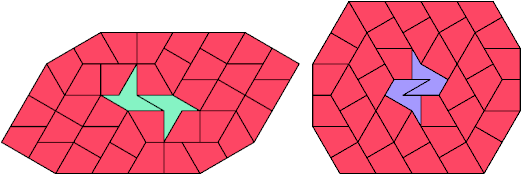
40 Tiles
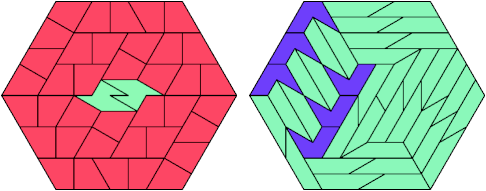
42 Tiles
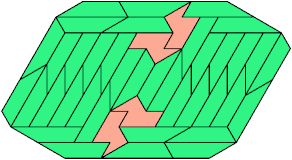
48 Tiles
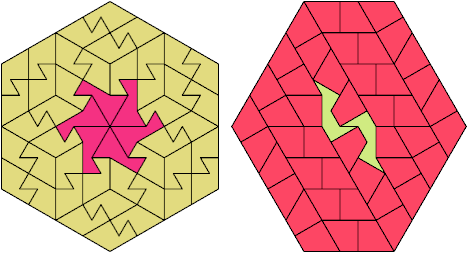
52 Tiles
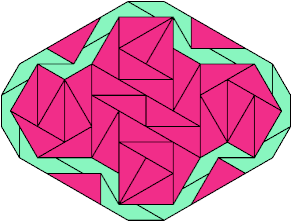
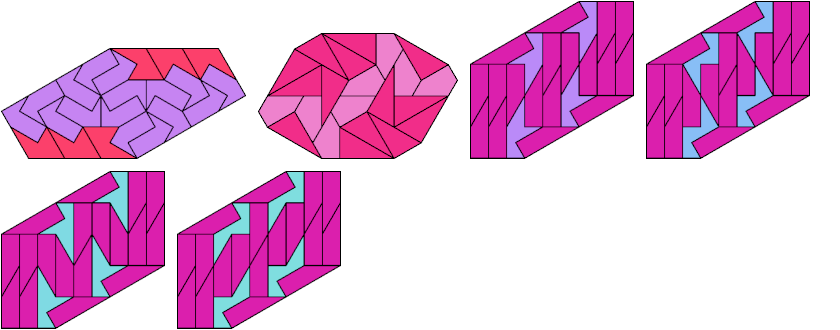
Lost Sheep
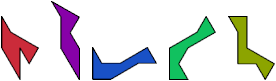
No convex pairing is known for any of these five tridrafters:
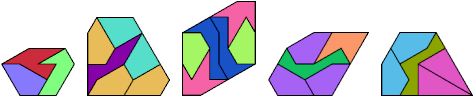
Each can form a convex shape with copies of two other tridrafters:
Last revised 2020-09-08.
Back to Polydrafter Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]