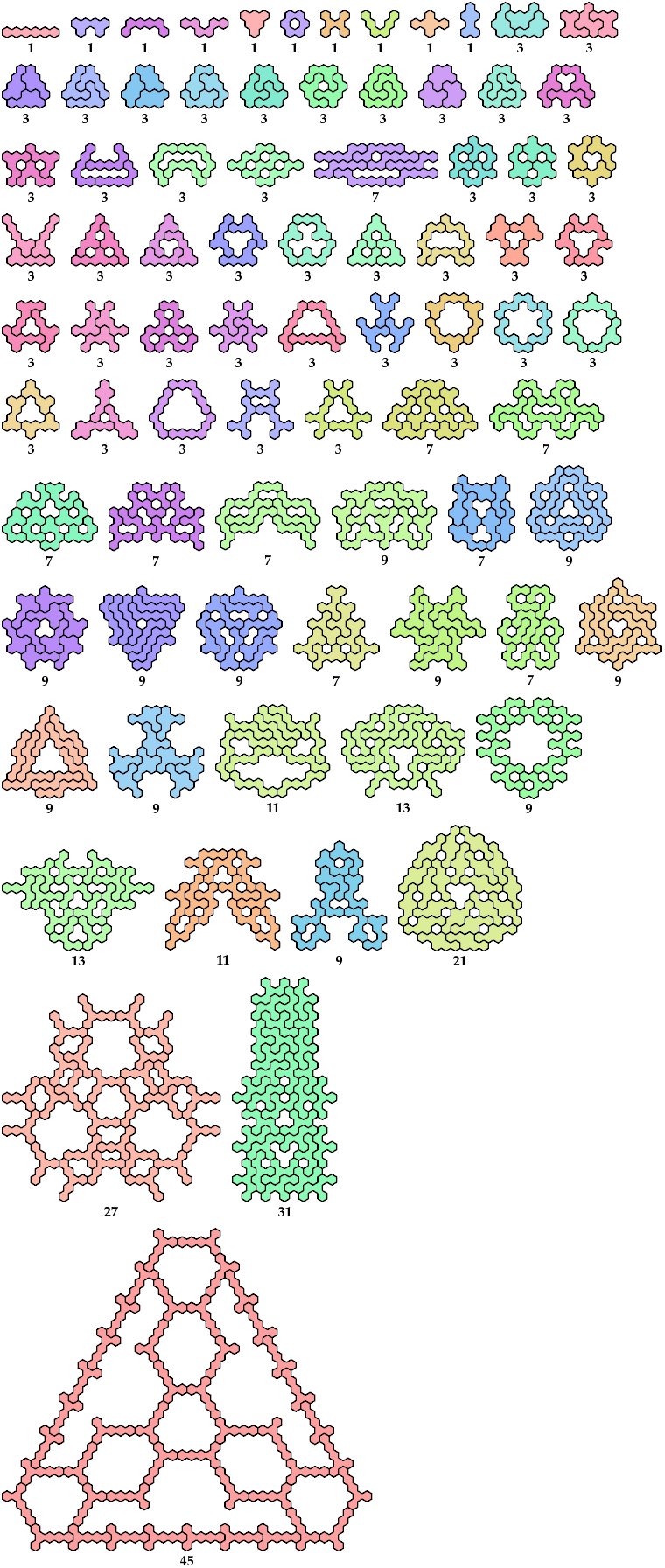
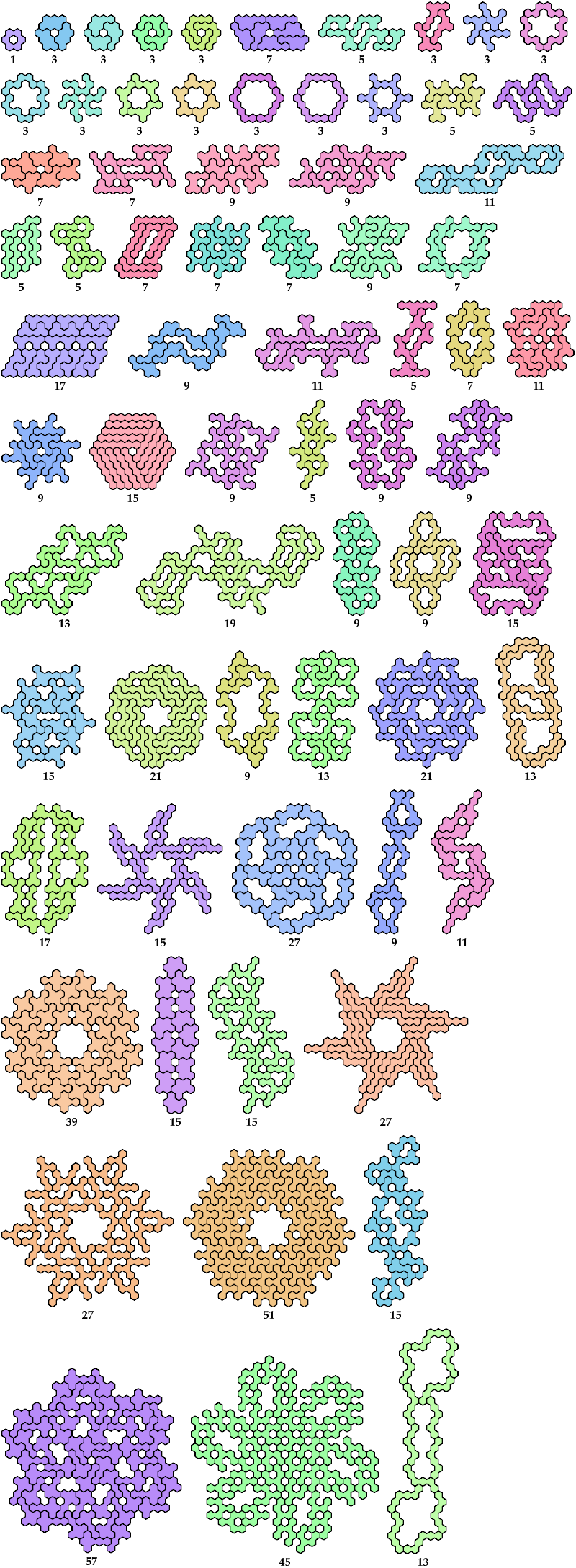
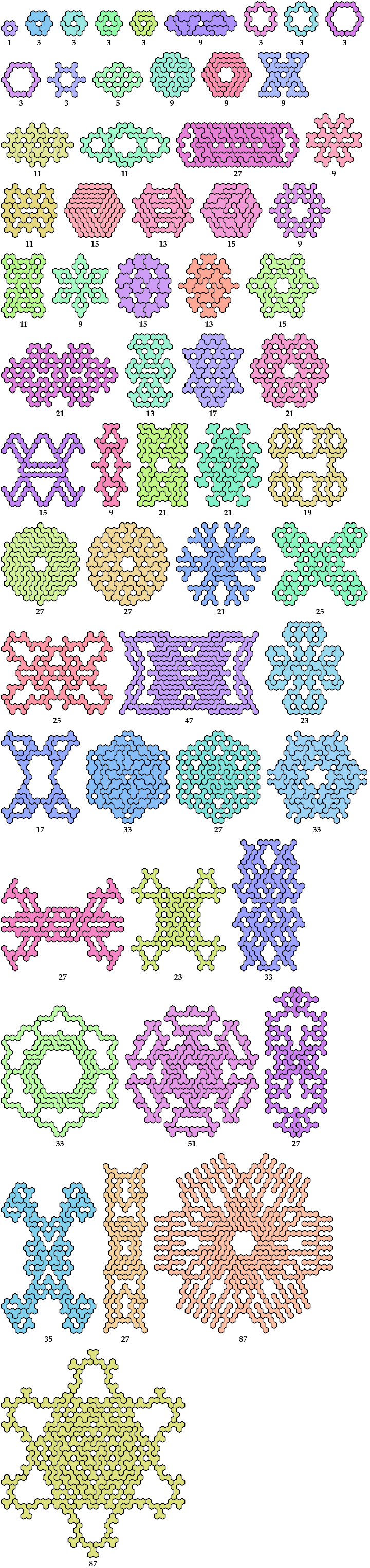
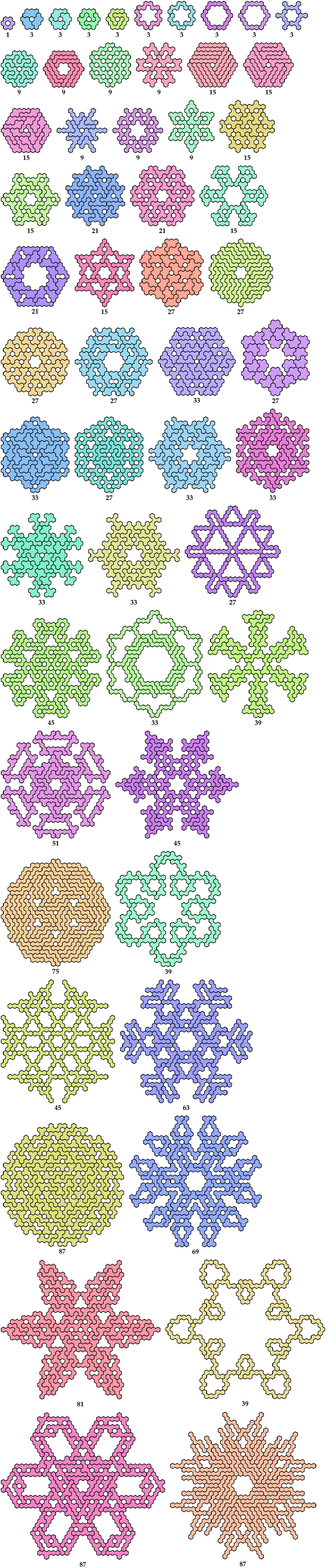
Hexahex Oddities
A hexahex oddity
is a figure with binary symmetry formed by an odd number of copies of
a hexahex.
Here are the minimal known oddities for hexahexes.
Please write if you find a smaller solution or solve an unsolved case.
Mike Reid
contributed improvements to some of these solutions.
For heptahex oddities, see
Heptahex Oddities.
For other orders of polyhexes, see
Trihex Oddities,
Tetrahex Oddities,
and
Pentahex Oddities.
[ Rowwise Bilateral
| Columnwise Bilateral
| Birotary on Edge
| Birotary on Cell
| Double Bilateral on Edge
| Double Bilateral on Cell
| Sextuple Rotary
| Full
]
Unsolved
Holeless Variants
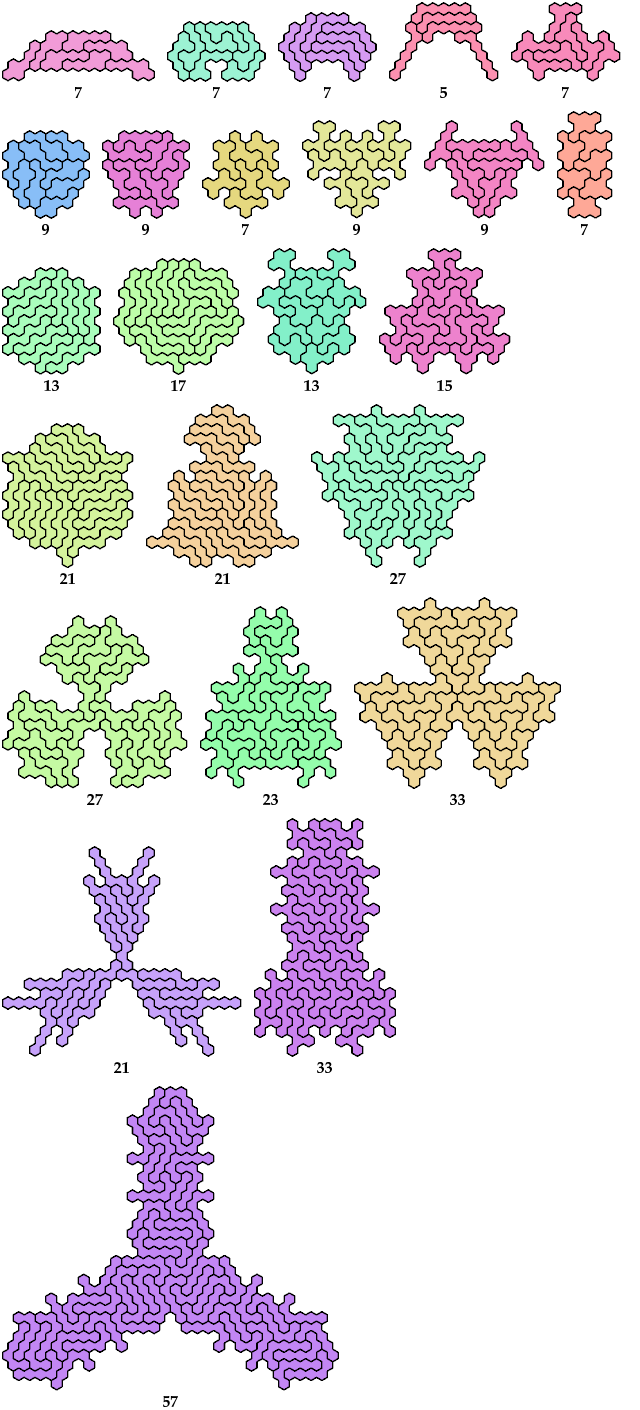

Unsolved

Impossible

Proof.
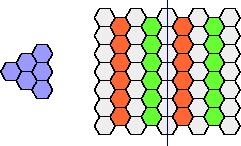 Color the cells of the plane as shown.
Assume without loss of generality that the median of the oddity passes
through a white column.
Each tile changes the balance of red and green cells by ±2.
Thus an odd number of tiles must have unequal numbers of
red and green cells.
But an oddity with columnwise symmetry must have equal numbers
of red and green cells.
Color the cells of the plane as shown.
Assume without loss of generality that the median of the oddity passes
through a white column.
Each tile changes the balance of red and green cells by ±2.
Thus an odd number of tiles must have unequal numbers of
red and green cells.
But an oddity with columnwise symmetry must have equal numbers
of red and green cells.
Holeless Variants
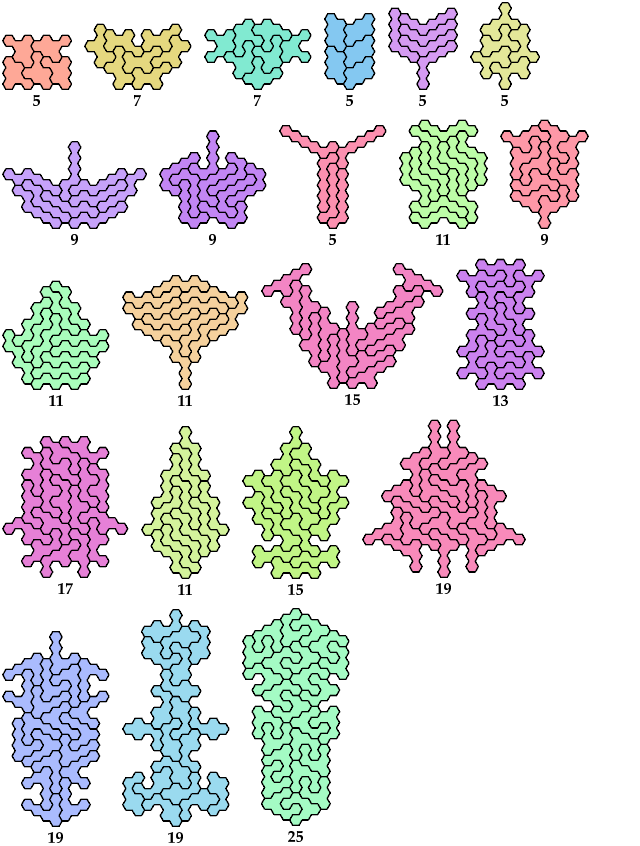

Unsolved

Impossible

Holeless Variants
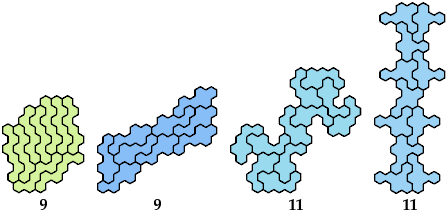
Unsolved

Impossible

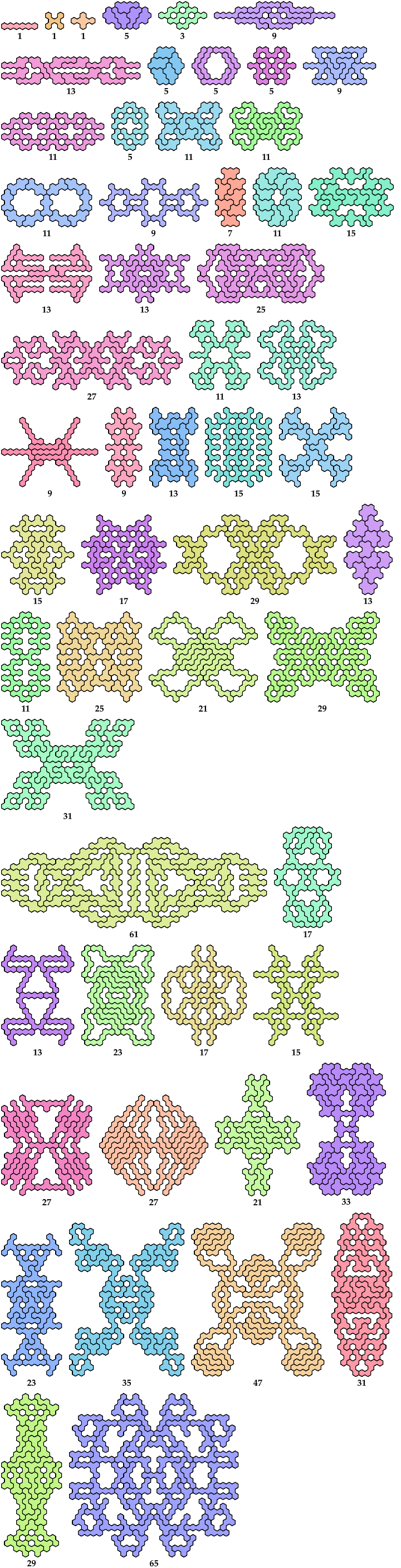
Unsolved

Impossible

Holeless Variants
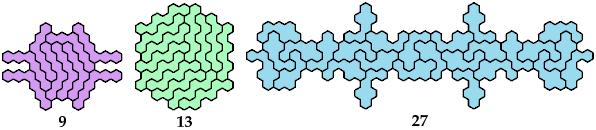
Unsolved

Impossible


Unsolved

Impossible

Unsolved

Impossible

Last revised 2024-10-01.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]




























