See also Rectifiable
Polyiamonds
at Andrew Clarke's Poly
Pages.

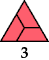

So far as I know, Mike Reid was the first to tile this triangle with the straight pentiamond.

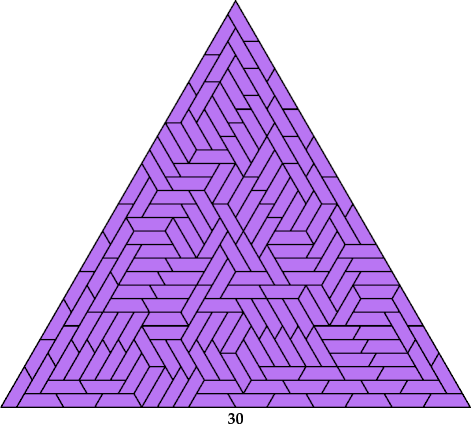
Go here for a tiling of a triangle with side 35. It has ternary symmetry except in the center. I found it in 2024.
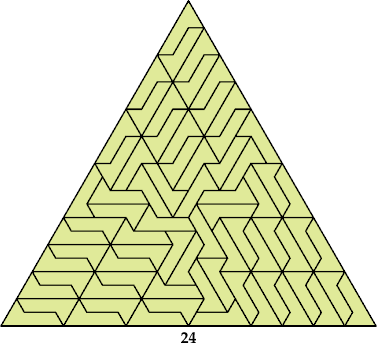
Soon after that, Patrick Mark Hamlyn posted to Puzzle Fun Facebook this tiling of a triangle with side 40.
The blue trapezoid below has a slant height of 15 and bases of lengths 7 and 22. It can be extended to any greater width as shown by the yellow tiles.

Such a trapezoid tiling can be adjoined to a tiling of a triangle with side s, where s ≧ 7, to tile a triangle with side s + 15. Thus every triangle whose side is 30 or greater and a multiple of 5 can be tiled with straight pentiamonds.
For more information about tiling a triangle with the straight pentiamond, see these links:
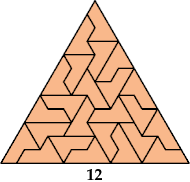
In this article at MathOverflow, Timothy Chow reported that Mike Reid stated at a 2007 conference in Duluth that this heptiamond can tile a triangle.
In this article at MathStackExchange, in 2021, Tom Sirgedas posted this tiling of a trapezoid with slant height 21 by straight heptiamonds. Its bases have lengths 203 and 224.
Sirgedas pointed out that this tiling can be padded horizontally to any greater width, and that such padded trapezoids can tile an expanded triamond.
In 2024, Carl Schwenke and Johann Schwenke shortened Sirgedas's trapezoid by 20 units. The resulting trapezoid has bases 183 and 204. To see it, click here.
We can apply Sirgedas's method of constructing a triamond as shown:

The height of the expanded triamond must be a multiple of 21. The smallest multiple of 21 greater than 183 is 189. So the smallest triamond that these trapezoids can form has slant height 189 and bases of lengths 189 and 378.
Three copies of the triamond can then form a triangle.
The resulting triangle has side 567. It has 45,927 tiles! That is too many to display here. But a smaller tiling may exist.
Last revised 2024-06-24.