Polyiamond Variegation

Introduction

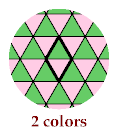
In his paper Polyominoes on a Multicolored Infinite Grid (in Thane Plambeck and Tomas Rokicki, eds., Barrycades and Septoku: Papers in Honor of Martin Gardner and Tom Rogers, Providence, 2020, MAA Press, Spectrum Series, v. 100, pp. 29–36), Hans Hung-Hsun Yu investigates how many colors are needed for the cells of the plane to ensure that a given polyomino has no two cells of the same color. Here I consider the corresponding problem for polyiamonds.

A polyiamond with k cells requires at least k colors. In the diagrams below, color counts that exactly meet this requirement appear in red.

For polyhexes, see Polyhex Variegation.

Diamond

For the diamond two colors suffice:

Triamond

For the triamond four colors are needed, to distinguish the cells of a triangle with side 2:

Tetriamonds

The same pattern admits two of the three tetriamonds:

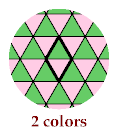
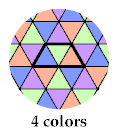
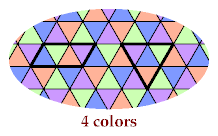
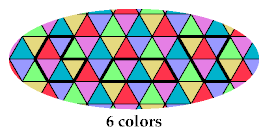
The third tetriamond requires 6 colors, to distinguish the cells of a hexagon with side 1:

Pentiamonds

The same pattern optimally admits the I, Q, and U pentiamonds:

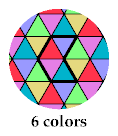
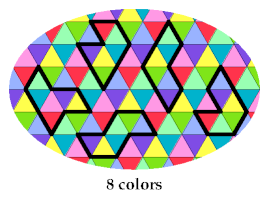
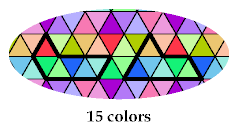
The fourth pentiamond requires 8 colors:

Hexiamonds

The pattern for the V tetriamond also admits five hexiamonds:

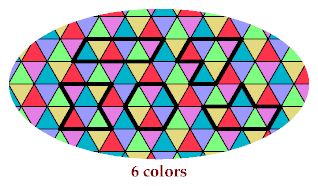
The pattern for the J pentiamond admits five other hexiamonds:

Here is the best pattern I have found for the remaining two hexiamonds.

Last revised 2018-07-19.

Back to Polyform Exclusion, Equalization, Variegation, and Integration < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]