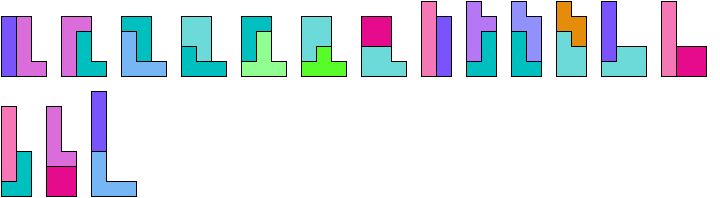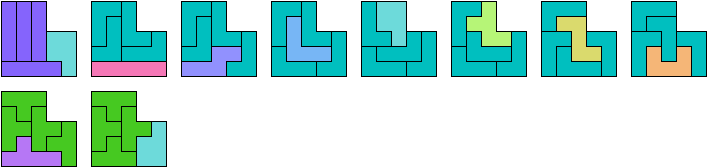Tiling an L Shape with a Tetromino and a Pentomino
Introduction
Here I show the smallest known L shapes, measured by area,
that can be tiled with copies of a given tetromino and a given pentomino,
using at least one of each.
If you find a smaller solution or solve an unsolved case,
please write.
9 Cells
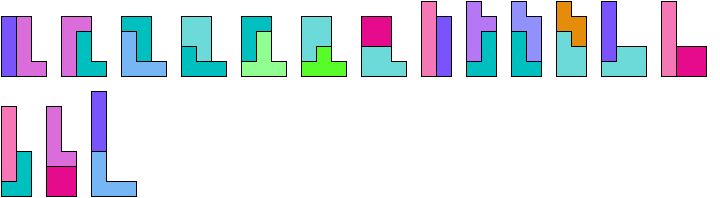
13 Cells

14 Cells

17 Cells

18 Cells

21 Cells

22 Cells

23 Cells

25 Cells

26 Cells

31 Cells

32 Cells

34 Cells

36 Cells

39 Cells

43 Cells

65 Cells

76 Cells

86 Cells

109 Cells

115 Cells

Unsolved
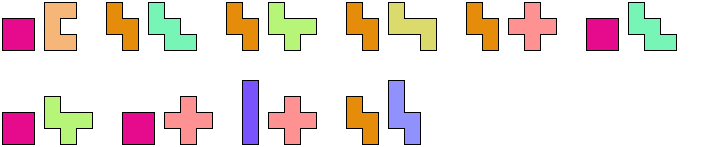
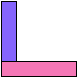
9 Cells
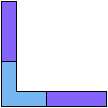
13 Cells
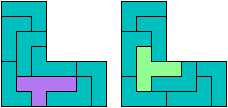
21 Cells
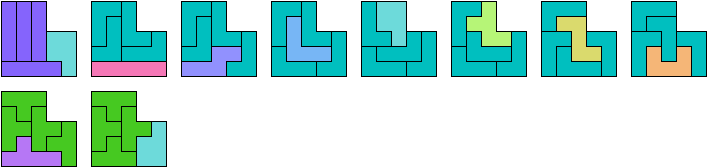
24 Cells

32 Cells

33 Cells
35 Cells

45 Cells

48 Cells

60 Cells

63 Cells
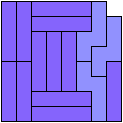
72 Cells
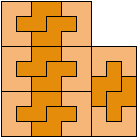
77 Cells
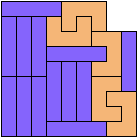
80 Cells
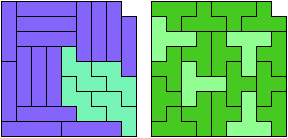
84 Cells
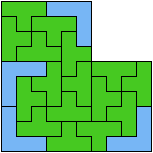
96 Cells
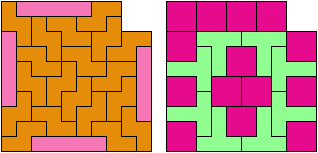
112 Cells
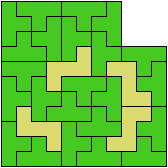
128 Cells
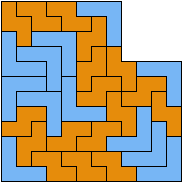
195 Cells
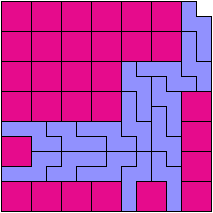
209 Cells

Last revised 2024-12-11.
Back to Polyomino and Polyking Tiling
< Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]