 | Pentomino Pair Odd Rectangles. Use copies of two pentominoes to tile a rectangle with odd area. |
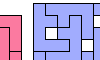
 | Polyomino Rectification with Holes. Tile a rectangle with a given polyomino, allowing isolated one-cell holes. |
 | Two-Pentomino Balanced Rectangles. Tile a rectangle with two pentominoes in equal quantities. |
 | Two-Pentomino Holey Balanced Rectangles. Tile a rectangle with two pentominoes in equal quantities, allowing one-cell holes. |
 | Tiling a Rectangle with a Pentomino and Isolated Trominoes. Tile a rectangle with copies of a pentomino and at least one tromino, not letting the trominoes touch. |
 | Tiling a Rectangle with a Hexomino and Isolated Trominoes. Tile a rectangle with copies of a hexomino and at least one tromino, not letting the trominoes touch. |
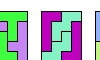 | Scaled Two-Pentomino Rectangles. Tile a rectangle with two pentominoes at various sizes. |
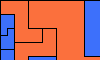 | Scaled Two-Pentomino Balanced Rectangles. Tile a rectangle with various sizes of two pentominoes in equal areas. |
 | Isolated Pentomino Pair Rectangles. Tile a rectangle with two pentominoes, isolating copies of one of them. |
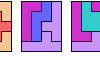 | Three-Pentomino Rectangles. Tile a rectangle with copies of three pentominoes. |
 | Scaled Three-Pentomino Rectangles. Tile a rectangle with three pentominoes at various sizes. |
 | Three-Pentomino Balanced Rectangles. Tile a rectangle with three pentominoes in equal quantities. |
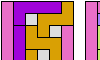 | Three-Pentomino Holey Balanced Rectangles. Tile a rectangle with three pentominoes in equal quantities, allowing one-cell holes. |
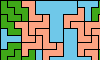 | Scaled Three-Pentomino Balanced Rectangles. Tile a rectangle with various sizes of three pentominoes in equal areas. |
 | Separated Pentominoes Tiling a Rectangle. Tile the largest possible rectangle with copies of three or four pentominoes, with no two copies of the same pentomino touching. |
 | Prime Rectangle Tilings for the Y Pentomino. Irreducible rectangles formed of Y pentominoes. |
 | Yin-Yang Dominoes. Arrange 10 of the 12 pentominoes to cover a bi-colored domino. |
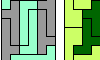 | Hexomino Pair Rectangles. Arrange copies of two hexominoes to form a rectangle. |
 | Tiling a Rectangle with a Hexomino and Isolated Monominoes. Tile the smallest possible rectangle with copies of a hexomino and the monomino, with no two monominoes touching. |
 | Scaled Hexomino Pair Rectangles. Arrange copies of two hexominoes at various scales to form a rectangle. |
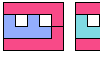 | Hexomino Pair Rectangles with Monomino Holes. Arrange copies of two hexominoes to form a rectangle that may have isolated one-cell holes. |
 | Hexomino Pair Rectangles with Domino Holes. Arrange copies of two hexominoes to form a rectangle that may have isolated two-cell holes. |
 | Hexomino Pair Rectangles with Monomino and Domino Holes. Arrange copies of two hexominoes to form a rectangle that may have isolated one-cell and two-cell holes. |
 | Prime Rectangles for Tetrakings.. For each tetraking, find the irreducible rectangles that it can tile. |
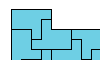 | Tiling an L Shape with a Polyomino. Tile an L-shaped polyomino with copies of a given polyomino. |
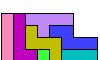 | Tiling an L Shape with the 12 Pentominoes. Tile various L-shaped polyominoes with the 12 pentominoes. |
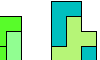 | Tiling an L Shape with a Tetromino and a Pentomino. Tile an L-shaped polyomino with copies of a given tetromino and pentomino. |
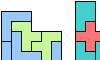 | L Shapes From Two Pentominoes. Form an L-shaped (hexagonal) polyomino with copies of two pentominoes, using at least one of each. |
 | Tiling an L Shape with a Tetromino and a Hexomino. Form an L-shaped (hexagonal) polyomino with copies of a tetromino and a hexomino, using at least one of each. |
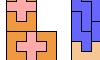 | Isolated Pentomino Pair L-Shapes. Form an L-shaped (hexagonal) polyomino with copies of two pentominoes, using at least one of each, and isolating the copies of one. |
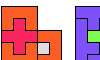 | Holey L Shapes From Two Pentominoes. Form an L-shaped (hexagonal) polyomino with copies of two pentominoes, using at least one of each, and allowing one-celled holes that do not touch the perimeter or one another. |
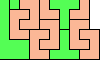 | Scaled Two-Pentomino L Shapes. Form an L-shaped (hexagonal) polyomino with copies of two pentominoes, letting them be enlarged, using at least one of each. |
 | Tiling an L Shape with a Hexomino and Isolated Trominoes. Form an L-shaped (hexagonal) polyomino with copies of a hexomino and at least one tromino, not letting the trominoes touch at edges or corners. |
 | L Shapes From Two Hexominoes. Form an L-shaped (hexagonal) polyomino with copies of two hexominoes, using at least one of each. |
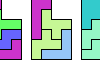 | Tiling an L Shape with Three Pentominoes. Tile an L-shaped polyomino with copies of three given pentominoes. |
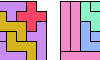 | Scaled Three-Pentomino L Shapes. Tile an L-shaped polyomino with copies of three given pentominoes at various sizes. |
| Tiling a Polyomino at Scale 2 with a Pentomino. |
| Tiling a Polyomino at Scale 2 with Two Pentominoes. |
| Tiling a Polyomino at Scale 2 with a Tetromino and a Pentomino. |
| Two-Pentomino Square Frames. |
| Three-Pentomino Square Frames. |
| Tiling Right Trapezoidal Polyominoes with Two Pentominoes. |
| Tiling Right Trapezoidal Polyominoes with Three Pentominoes. |
| Tiling a Blunt Pyramid with Two Polyominoes. |
| Full Symmetry from the Twelve Pentominoes. |
| Tiling a Beveled Rectangle with Polyominoes. |
 | Tiling Strips with Polyominoes. Tiling straight, bent, branched, and crossed infinite strips with polyominoes of orders 1 through 6. |
 | Uniform Polyomino Stacks. Join copies of a polyomino to make a figure with uniform row width. |
 | Globular 3-4-5 Pentomino Dissections. Dissect a pentomino at scale 5 into two copies of the pentomino at scales 3 and 4, with the pentomino at scale 4 unbroken. |
 | Perfect Polyominoes. Polyominoes that can be formed by joining all the smaller polyominoes that can tile them. |
 | Polyomino Bireptiles. Join two copies of a polyomino, then dissect the result into equal smaller copies of it. |
 | Covering a Rectangle with Copies of a Polyomino. Find the largest rectangles that copies of a polyomino can cover without overlapping. |
 | A Pentomino Christmas Card. Pentomino art with an unexpected aftermath. |
